Haryana Board (HBSE) Class 9 Maths Question Paper 2022 Answer Key. Haryana Board Class 9th Maths Solved Question Paper 2022 PDF Download. BSEH Board Class 9th Question Paper 2022 Pdf Download with Answer. HBSE Class 9 Maths Previous Year Question Paper with Answer. HBSE 9th Maths Solved Question Paper 2022. HBSE 9th Class Maths Solved Question Paper 2022.
HBSE Class 9 Maths Question Paper 2022 Answer Key
Q1. The value of (3 + √3)(2 + √2) is …………
Ans. 6 + 3√2 + 2√3 + √6
Q2. Which of the following is not a rational number ?
(A) √2
(B) 0
(C) √4
(D) √-16
Ans. (A) √2
Q3. Value of 16^¾ is :
(A) 4
(B) 12
(C) 8
(D) 48
Ans. (C) 8
Power of 16 is ¾ = (2⁴)^¾ = 2³ = 8
Q4. What will be get after rationalize the denominator of 1/(√5+√2) ?
Sol.
1/(√5+√2) × (√5-√2)/(√5-√2)
= (√5-√2) ÷ [(√5)²-(√2)²]
= (√5-√2) ÷ (5-2) = (√5-√2)/3
Q5. Which of the type is polynomial t² – 4 ?
(A) Binomial
(B) Monomial
(C) Trinomial
(D) None of these
Ans. (A) Binomial
Q6. The degree of 5x³ + 4x² + 7x is :
(A) 1
(B) 2
(C) 3
(D) 4
Ans. (C) 3
Q7. The value of (99)³ is :
(A) 970289
(B) 970299
(C) 970389
(D) 970489
Ans. (B) 970299
Q8. The factors of 64m³ – 343n³ are …………
Sol.
Using formula, a³ – b³ = (a – b)(a² + b² + ab)
64m³ – 343n³ = (4m)³ – (7n)³
= (4m – 7n)[(4m)² + (7n)² + (4m)(7n)]
= (4m – 7n)(16m² + 49n² + 28mn)
Q9. The value of k is, if x – 1 is a factor of p(x) = kx² – √2x + 1 ?
(A) √2 + 1
(B) -1 + √2
(C) √2 – 1
(D) -√2 – 1
Ans. (C) √2 – 1
x – 1 = 0 then x = 1
p(x) = kx² – √2x + 1
p(1) = k(1)² – √2(1) + 1 = 0
k – √2 + 1 = 0
k = √2 – 1
Q10. Product of (x + 4)(x + 10) will be what ?
Sol.
(x + 4)(x + 10) = x² + 10x + 4x + 40 = x² + 14x + 40
Q11. The graph of line x + y = 7 intersects the x-axis at which point ?
Sol.
x + y = 7
y = 0 (intersect the x-axis)
x + 0 = 7
x = 7
Coordinates (x, y) = (7, 0)
Q12. Solution of equation 2x + 1 = x + 3 is ………….
Sol.
2x + 1 = x + 3
2x – x = 3 – 1
x = 2
Q13. Graph of x = 2 is a line :
(A) Parallel to x-axis
(B) Parallel to y-axis
(C) Passes through origin
(D) None
Ans. (B) Parallel to y-axis
Q14. Point (-1, 4) lies on which quadrant ?
(A) I
(B) IV
(C) II
(D) III
Ans. (C) II
Q15. Point (0, -3) lies on :
(A) x-axis
(B) y-axis
(C) 1st quadrant
(D) 2nd quadrant
Ans. (B) y-axis
Q16. The abscissa and ordinate of (6, −4 ) is ………….
Ans. Abscissa (x) = 6 and ordinate (y) = -4
Q17. Write the name of the point where these two lines intersect.
Ans. Origin (0, 0)
Q18. If point M, is the mid point of hypotenuse AC of right angled ∆ABC, then BM = 1/2 :
(A) AC
(B) AB
(C) BC
(D) None of these
Ans. (A) AC
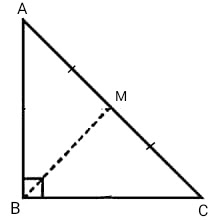
Q19. ∆ABC is a right angled triangle in which ∠A = 90° and AB = AC. What is the value of ∠B and ∠C ?
Sol.
∠A + ∠B + ∠C = 180°
90° + x + x = 180° (∠B = ∠C because AB = AC)
2x = 180° – 90°
x = 90°/2 = 45°
∠A = ∠B = x = 45°
Q20. The triangle formed by joining the mid-points of the sides of an isosceles triangle is ……………
Ans. isosceles triangle
Q21. The angles of a quadrilateral are in the ratio 3 : 4 : 5 : 6. The respective angles of the quadrilateral are :
(A) 60°, 80°, 100°, 120°
(B) 120°, 100°, 80°, 60°
(C) 120°, 60°, 80°, 100°
(D) 80°, 100°, 120°, 60°
Ans. (A) 60°, 80°, 100°, 120°
Sum of all angles of a quadrilateral = 360°
3x + 4x + 5x + 6x = 360°
18x = 360°
x = 360/18 = 20
3x = 3 × 20 = 60°
4x = 4 × 20 = 80°
5x = 5 × 20 = 100°
6x = 6 × 20 = 120°
Q22. In fig., A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, then ∠ADC will be :
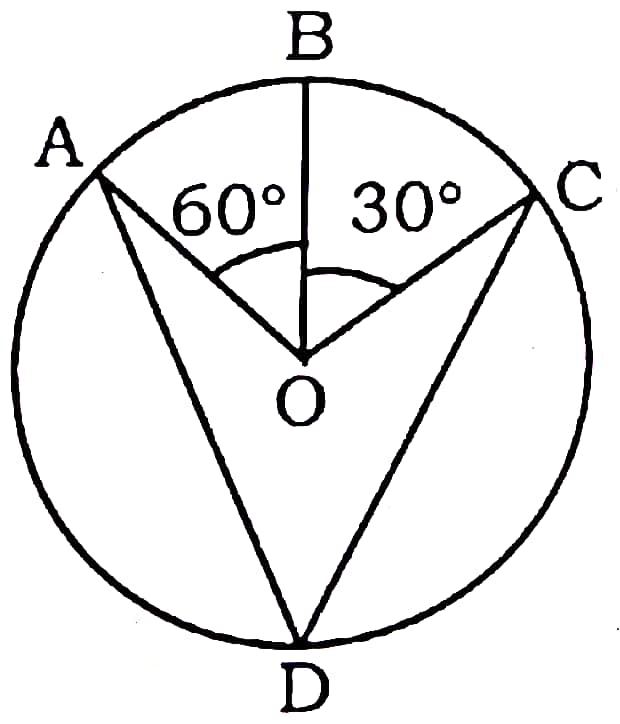
Ans.
∠AOC = ∠AOB + ∠BOC = 60° + 30° = 90°
∠ADC = ½∠AOC = ½ × 90° = 45°
Q23. One and only one circle can pass through from how much non-collinear points ?
(A) Three
(B) Four
(C) Five
(D) Six
Ans. (A) Three
Q24. In a pair of set square angle of one triangle are :
(A) 30°, 40°, 100°
(B) 60°, 30°, 90°
(C) 30°, 30°, 45°
(D) None of these.
Ans. (B) 60°, 30°, 90°
Q25. To draw the perpendicular bisector of the segment AB, we open the compass how much ?
Ans. More than half of AB (radius > AB/2)
Q26. To construct a triangle we must know at least its …………. parts.
Ans. Three
Q27. Two sides of a triangle are 8 cm and 11 cm having perimeter 32 cm, then its semi perimeter is :
(A) 4 cm
(B) 13 cm
(C) 14 cm
(D) 16 cm
Ans. (D) 16 cm
Semi Perimeter = Perimeter/2 = 32/2 = 16 cm
Q28. The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m that area of plot are :
(A) 1500√3 m²
(B) 1200√3 m²
(C) 1800√3 m²
(D) 1600√3 m²
Ans. (A) 1500√3 m²
a = 3x, b = 5x, c = 7x
Perimeter (P) = 300 m
Semi Perimeter (s) = 300/2 = 150 m
P = a + b + c
3x + 5x + 7x = 300
15x = 300
x = 300/15 = 20
a = 3x = 3 × 20 = 60 m
b = 5x = 5 × 20 = 100 m
c = 7x = 7 × 20 = 140 m
Using Heron’s Formula,
Area of triangle = √s(s-a)(s-b)(s-c)
= √150(150-60)(150-100)(150-140)
= √150(90)(50)(10) = √3×50×9×10×50×10 = 1500√3 m²
Q29. What is the area of a triangle when its base and height is known ?
Ans.
Area of triangle = ½ × base × height = ½bh
Q30. If each edge of a cube is ‘a’, then the surface area of the cube is ………….
Ans.
Surface area (SA) = Total surface area (TSA) = 6a²
Lateral surface area (LSA) = 4a²
Q31. The volume of a sphere is 524 cm³. The diameter of sphere is :
(A) 4 cm
(B) 10 cm
(C) 3 cm
(D) 6 cm
Ans. (B) 10 cm
Volume of a sphere, V = 4/3 × πr³
4/3 × 22/7 × r³ = 524
r³ = 524 × 7/22 × 3/4 = 125 (approx.)
r = 5
d = 2r = 2 × 5 = 10 cm
Q32. The height of a cone is 15 cm. If its volume is 1570 cm³, the radius of it base is ? (Take π = 3.14)
Sol.
Volume of cone (V) = ⅓πr²h
⅓ × 3.14 × r² × 15 = 1570
r² = (1570×3) ÷ (3.14×15) = 4710 ÷ 47.1 = 100
r = √100 = 10 cm
Q33. The total surface area of a cylinder is ………..
Ans. TSA of cylinder = 2πrh + 2πr² = 2πr(r+h)
Q34. The base radius of a cone is 11.3 cm and curved surface is 355 cm². Its slant height is : (Take π = 355/113)
(A) 11 cm
(B) 9 cm
(C) 5 cm
(D) 10 cm
Ans. (D) 10 cm
CSA = πrl
355/113 × 11.3 × l = 355
Slant height (l) = 355 × 113/355 × 1/11.3 = 10 cm
Q35. Class mark of class 140–150 is …………
Ans. Class mark or mid value = (140+150)/2 = 290/2 = 145
Q36. The marks (out of 10) obtained by 20 students are as follows :
9, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9
The modal marks are :
(A) 7
(B) 9
(C) 3
(D) 10
Ans. (B) 9
Mode = most repeated data
Q37. The following number of goals were scored by a team in a series of 10 matches :
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
Find median of these scores.
Sol.
Ascending order, 0, 1, 2, 3, 3, 3, 3, 4, 4, 5
Median = (3+3)/2 = 6/2 = 3
Q38. After rolling a die 500 times the frequency of coming 2 is 200. What is probability of throwing 2 ?
(A) 3/5
(B) 2/5
(C) 1
(D) 4/5
Ans. (B) 2/5
P(2) = 200/500 = 2/5
Q39. Probability of an impossible event is always :
(A) 1
(B) 0
(C) 2
(D) 1/2
Ans. (B) 0
Q40. A batsman hits boundries 15 out of 50 balls. What is the probability that he will not hit boundary?
Sol.
Total = 50
hits boundaries = 15
not hit boundaries = 50 – 15 = 35
P(not hit boundaries) = 35/50 = 7/10
Subjective Questions
Q2. Express 0.99999…. in the form p/q
Sol.
x = 0.99999…. (i)
10x = 9.99999…. (ii)
Subtract eqn.(i) from (ii),
9x = 9
x = 9/9 = 1
Q3. Draw the graph of following linear equation in two variables :
3 = 2x + y
Sol.
when x = 0, then y = 3
when x = 1, then y = 1
using co-ordinates (0, 3) and (1, 1)
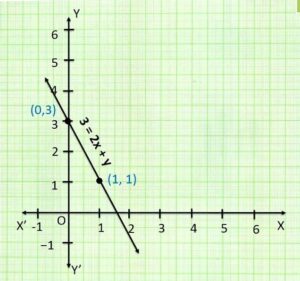
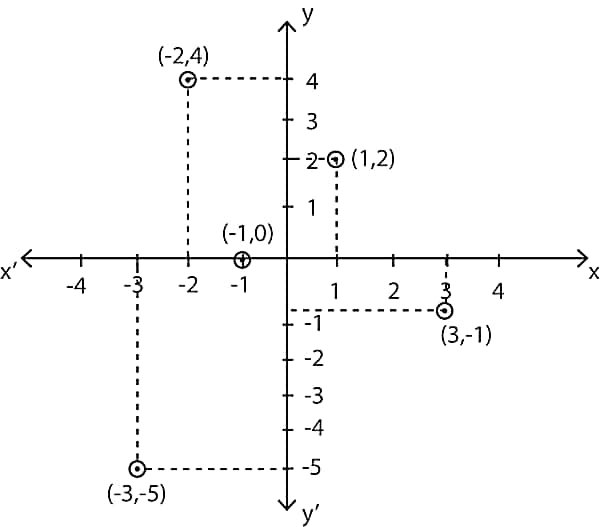
Q4. In which quadrant or on which axis do each of the points (-2, 4), (3, −1), (−1, 0), (1, 2), (-3, -5) lie ? Verify your answer by locating them on the Cartesian plane.
Sol.
The point (-2, 4) lies in the II quadrant
The point (3, -1) lies in the IV quadrant
The point (-1, 0) lies on the x-axis
The point (1, 2) lies in the I quadrant
The point (-3, -5) lies in the III quadrant.
Q5. Find the angles formed at the centre by the sides of regular circular pentagon.
Sol.
Complete angle = 360°
Each angle at center = 360°/5 = 72°
Q6. In a cricket match a lady batsman hits a boundary 6 times out of 30 balls the plays. Find the probability that she will not hit boundary in the next ball.
Sol.
Total = 30
hit boundary = 6
not hit boundary = 30 – 6 = 24
P(not hit boundary) = 24/30 = 4/5
Q7. Factorise :
x³ + 13x² + 32x + 20
= x³ + x² + 12x² + 12x + 20x + 20
= x²(x+1) + 12x(x+1) + 20(x+1)
= (x+1)(x² + 12x + 20)
= (x+1)(x² + 2x + 10x + 20)
= (x+1)[x(x+2) + 10(x+2)]
= (x + 1)(x + 2)(x + 10)
Q8. Show that the angles of an equilateral triangle are 60° each.
Sol.
Take a equilateral ∆ABC,
so, ∠A = ∠B = ∠C = x
∠A + ∠B + ∠C = 180°
x + x + x = 180°
3x = 180°
x = 180°/3 = 60°
∠A = ∠B = ∠C = 60°
Q9. Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.
Sol.
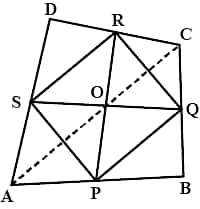
SR || AC and SR = ½AC (using Mid-Point theorem)
PQ || AC and PQ = ½AC (using Mid-Point theorem)
so, SR || PQ and SR = PQ
PQRS is Parallelogram (if one pair is parallel and equal in quadrilateral, then it is Parallelogram)
PR & SQ bisect each other (because diagonal of Parallelogram PQRS bisect each other).
Q10. Construct a triangle ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 3.5 cm.
Sol.

Steps of construction :
(i) Draw base BC of length 8cm
(ii) Now, let’s draw ∠B = 45°, Let the ray be BX
(iii) Open the compass to length AB-AC=3.5 cm. Since AB−AC=3.5cm is positive. So, BD will be above line BC. From point B as center, cut an arc on ray BX. Let the arc intersect BX at D.
(iv) Join CD
(v) Now, we will draw perpendicular bisector of CD
(vi) Mark point A where perpendicular bisector intersects BD
(vii) Join AC
So, ∆ABC is the required triangle.
Q11. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Sol.
Perimeter= 42 cm
Semi Perimeter, s = 42/2 = 21 cm
a = 18 cm
b = 10 cm
c = 42 – (18+10) = 42 – 28 = 14 cm
Using Heron’s Formula,
Area = √s(s-a)(s-b)(s-c) = √21(21-18)(21-10)(21-14)
= √21(3)(11)(7) = 21√11 cm²
Q12. If two sides of a cyclic quadrilateral are parallel, prove that :
(i) remaining two sides are equal and
(ii) both diagonals are equal
Sol.
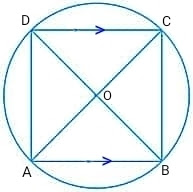
(i) Given AB || DC
Therefore ∠BAC =∠DCA (alternate angles)
Chord AD subtends ∠DCA on circumference.
Chord BC subtends ∠CAB on circumference.
so, AD = BC (since equal chords subtend equal angles on the circumference)
(ii) In ∆ADB and ∆ABC,
AB =AB (common)
AD = CB (proved above)
∠ACB = ∠ADB (angles in the same segment)
∆ADC ≅ ∆ABC (SAS)
so, AC = DB (CPCT)
OR
ABC is a triangle right angled at C. A line through the mid point M of hypotenuse AB and parallel to BC intersects AC at D. Show that :
(i) D is the mid point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½AB
Sol.
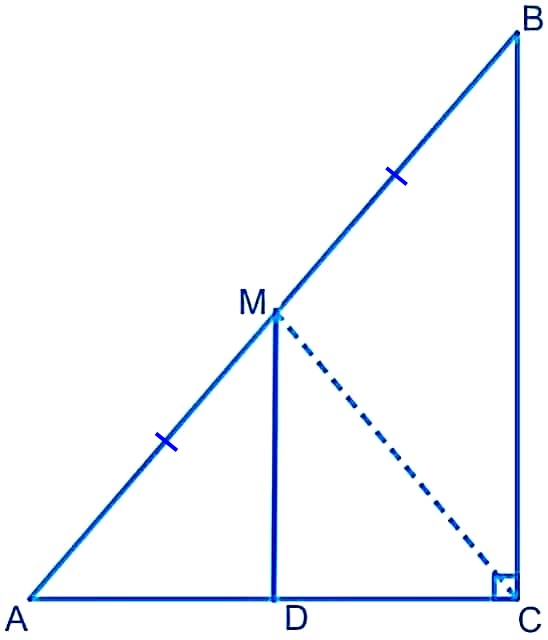
By converse of mid-point theorem, we know that a line drawn through the mid-point of any side of a triangle that is parallel to another side bisects the third side.
(i) In ΔABC,
It is given that M is the mid-point of AB and MD || BC.
∴ D is the mid-point of AC [Converse of mid-point theorem]
(ii) As DM || CB and AC is a transversal,
∠MDC + ∠DCB = 180° [Co-interior angles]
∠MDC + 90° = 180°
∠MDC = 90°
∴ MD ⊥ AC
(iii) Join MC
In ΔAMD and ΔCMD,
AD = CD (D is the mid-point of side AC)
∠ADM = ∠CDM (Each 90°)
DM = DM (Common)
∴ ΔAMD ≅ ΔCMD (By SAS congruence rule)
Therefore, AM = CM (By CPCT)
However, we also know that AM = ½AB (M is the mid-point of AB)
∴ CM = AM = ½AB
Q13. The paint in a certain container is sufficient to paint an area equal to 9.375 m². How many bricks of dimensions 22.5cm x 10cm x 7.5cm can be painted out of this container ?
Sol.
Volume of paint = 9.375 m³ = 9.375 × 100 × 100 = 93750 cm³
Dimension of brick = 22.5 cm×10 cm×7.5 cm
Here, l = 22.5 cm, b = 10 cm, h = 7.5 cm
Total surface area of a brick = 2(lb + bh + lh) cm²
= 2(22.5×10 + 10×7.5 + 22.5×7.5) cm²
= 2(225 + 75 + 168.75) cm²
= 2×468.75 cm² = 937.5 cm²
Number of bricks can be painted = 93750/937.5 = 100 bricks
OR
A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and diameter of graphite is 1 mm. If the length of the pencil is 14 cm, find the volumes of the wood and that of the graphite.
Sol.
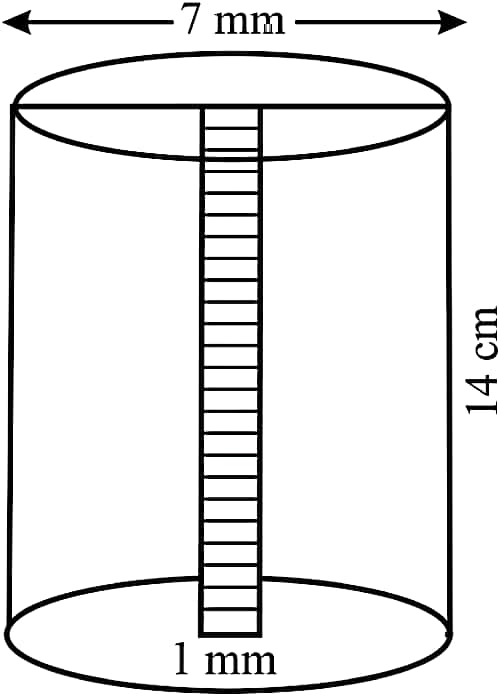
Diameter of the pencil = 7 mm
Radius (R) = 7/2 mm = 3.5/10 cm = 0.35 cm
h = 14 cm
Volume of the pencil = πR²h
= 22/7 × 0.35 cm × 0.35 cm × 14 cm = 5.39 cm³
Diameter of the graphite = 1 mm
Radius (r) = 1/2 mm = 0.5/10 cm = 0.05 cm
h = 14 cm
Volume of the graphite = πr²h
= 22/7 × 0.05 cm × 0.05 cm × 14 cm = 0.11 cm³
Volume of wood = Volume of the pencil – Volume of the graphite
= 5.39 cm³ – 0.11 cm³ = 5.28 cm³
Q14. A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced. The table shows the result of 1000 cases:
![]()
If you buy a tyre of this company, what is the probability that :
(i) It will need to be replaced before it has covered 4000 km ?
Ans. P(less than 4000km) = 20/1000
(ii) It will last more than 9000 km?
Ans. P(more than 9000km) = 770/1000
(iii) It will need to be replaced after it has covered somewhere between 4000 km and 14000 km ?
Ans. P(between 4000km and 14000km) = 535/1000
