Haryana Board (HBSE) Class 11 Physics SAT-1 Question Paper 2025 Answer Key. Get the Students Assessment Test (SAT) Class 11 Physics question paper with complete solution, accurate answer key, and expert preparation tips. The Haryana Board of School Education (HBSE) conducts SAT as an important assessment for Class 11 students. Best resource for Haryana Board Class 11 SAT Physics exam practice, quick revision, and scoring better marks.
HBSE Class 11 Physics SAT-1 Question Paper 2025 Answer Key
Instructions :
• All questions are compulsory.
• Questions (1-9) carry 1 mark each.
• Questions (10-12) carry 2 marks each.
• Questions (13-14) carry 3 marks each.
• Question (15) case study, carry 4 marks.
• Questions (16-17) carry 5 marks each.
1. Unit vector along the vector 4î + 3ĵ is :
(A) (4î + 3ĵ)/5
(B) (4î + 3ĵ)
(C) (4î + 3ĵ)/6
(D) (4î + 3ĵ)/10
Answer – (A) (4î + 3ĵ)/5
Now |A| = √42+32 = √16+9 = √25 = 5
Unit vector of A is A / |A| = (4î + 3ĵ)/5
2. The dimensional formula [MLT–2] matches with the dimensional formula of :
(A) Force
(B) Pressure
(C) Displacement
(D) Strain
Answer – (A) Force
3. 5.74 g of a substance occupies 1.2 cm3. Express its density by keeping the significant figures in view.
(A) 4.839 g cm–3
(B) 4.379 g cm–3
(C) 4.783 g cm–3
(D) 4.784 g cm–3
Answer – (C) 4.783 g cm–3
Density (ρ) = Mass/Volume = 5.74/1.2 = 4.783 g cm–3
4. A particle moves in a plane with constant acceleration in a direction with some initial velocity perpendicular to acceleration. The path of the particle will be :
(A) A parabola
(B) An ellipse
(C) A straight line
(D) An arc of a circle
Answer – (A) A parabola
5. Slope of velocity-time graph for a body in uniform motion is …………….
Answer – Zero
6. Area under velocity-time curve = ……………..
Answer – Displacement
7. Is the statement “Spring force is Conservative” true?
Answer – True
8. The product of force and time duration is known as …………….
Answer – Impulse
9. Assertion (A) : Two particles of different mass, projected with same velocity at same angles. The maximum height attained by both the particles will be the same.
Reason (R) : The maximum height of a projectile is independent of particle mass.
(A) Both Assertion and Reason are true, and Reason is the correct explanation of Assertion.
(B) Both Assertion and Reason are true, and Reason is not the correct explanation of Assertion.
(C) Assertion is true but Reason is false.
(D) Assertion is false but Reason is true..
Answer – (A) Both Assertion and Reason are true, and Reason is the correct explanation of Assertion.
10. If F = a + bx, where F is the force, x is the distance. Derive the dimensions of a and b.
Answer – Here, F has [MLT–2], x has [L]
By principle of homogeneity,
[a] = [F] = [MLT–2]
[b] = [F] / [x] = [MLT–2] / [L] = [ML0T–2]
11. Define Instantaneous Velocity and write its unit.
Answer – Instantaneous velocity is the velocity of an object at a specific point in time, indicating both the speed and direction of motion at that exact moment. The SI unit for instantaneous velocity is meters per second (m/s), which is the same unit as speed.
12. Rain is falling vertically with a speed of 36 ms–1. Wind starts blowing after some time with a speed of 12√3 ms–1 in east to west direction. In which direction should a boy waiting at a bus stop hold his umbrella?
Answer – The angle (θ) between the resultant velocity and the vertical (rain’s direction) can be found using trigonometry. In this case, the tangent of the angle (tan θ) is equal to the ratio of the wind’s speed (east-west) to the rain’s speed (vertical).
tanθ = (wind speed) / (rain speed)
tanθ = 12√3 / 36
tanθ = √3 / 3 = 1/√3
θ = 30°
Since the wind is blowing from east to west, the umbrella should be tilted towards the west to effectively block the rain and wind.
13. State and prove Law of conservation of linear momentum.
Answer – The law of conservation of linear momentum states that the total momentum of an isolated system remains constant if no external forces act on it.
• Proof : Consider two bodies A and B of masses m1 and m2 moving in the same direction with uniform velocities u1 and u2 respectively. After the collision let their uniform velocities be v1 and v2. Let ‘t’ be the time of impact.
Change in momentum of A = m1v1 – m1u1
Rate of change of momentum of A (F1) = (m1v1 – m1u1) / t
Change in momentum of B = m2v2 – m2u2
Rate of change of momentum of A (F2) = (m2v2 – m2u2) / t
F1 = – F2
(m1v1 – m1u1) / t = – (m2v2 – m2u2) / t
m1u1 + m2u2 = m1v1 + m2v2
i.e., Total momentum before collision = Total momentum after collision. Hence the momentum is conserved.
14. State and prove Work Energy Theorem.
Answer – The work done by the net force on a body is equal to the change in its kinetic energy.
Wnet = ∆KE = Kf – Ki = ½mv2 – ½mu2
Proof :
By definition, the work done by a constant net force is :
Wnet = Fnet × S
According to Newton’s Second Law of Motion :
Fnet = ma
Substitute this into the work equation :
Wnet = (ma) × S ……..(i)
For uniformly accelerated motion, the third equation of motion is:
v2 = u2 + 2aS
aS = (v2 – u2)/2 ……..(ii)
Substitute the expression for aS from equation (ii) into the work done equation (i) :
Wnet = m(v2 – u2)/2
Wnet = ½mv2 – ½mu2
Wnet = KEf – KEi = ∆KE
Work done = Change in Kinetic Energy
Hence, the Work-Energy Theorem is proved.
15. CASE STUDY : In physics, we can classify quantities as scalars or vectors. Basically, the difference is that a direction is associated with a vector but not with a scalar. A scalar quantity is a quantity with magnitude only. It is specified completely by a single number, along with the proper unit. Examples are: the distance between two points, mass of an object, the temperature of a body and the time at which a certain event happened. The rules for combining scalars are the rules of ordinary algebra. Scalars can be added, subtracted, multiplied and divided just as the ordinary numbers. A vector quantity is a quantity that has both a magnitude and a direction and obeys the triangle law of addition or equivalently the parallelogram law of addition. So, a vector is specified by giving its magnitude by a number and its direction. Some physical quantities that are represented by vectors are displacement, velocity, acceleration and force.
Questions :
(i) Force is an example of :
(A) Scalar
(B) Vector
(C) Tensor
(D) None of these
Answer – (B) Vector
(ii) Mass of an object is :
(A) Scalar
(B) Vector
(C) Tensor
(D) None of these
Answer – (A) Scalar
(iii) Define scalar or vector quantity.
Answer – Scalar quantity has only magnitude, while Vector quantity has both magnitude and direction.
(iv) Do vectors follow the Triangle Law of vector Addition?
(A) Yes
(B) No
(C) Can’t be said
Answer – (A) Yes
16. Derive the formulae for : (i) Time of flight, (ii) horizontal range, (iii) Maximum Height of a projectile thrown with a velocity u at an angle θ from the horizontal.
Answer : Time of Flight – The time of flight is the total time taken by the projectile to complete its motion through the air, that is, the time interval between its projection and the moment it returns to the same vertical level from which it was projected.
T = 2usinθ / g
• Horizontal Range – The horizontal range of a projectile is the total horizontal distance covered by it between the point of projection and the point where it again reaches the same vertical level.
R = u2sin2θ / g
• Maximum Height – The maximum height is the greatest vertical distance attained by the projectile above the horizontal plane during its motion.
Hmax = u2sin2θ / 2g
OR
State parallelogram law of vector addition. Derive expression for magnitude and direction of Resultant vector analytically.
Answer – The Parallelogram Law of vector addition states that if two vectors acting at a point are represented by the adjacent sides of a parallelogram in magnitude and direction, then their resultant vector is represented by the diagonal of the parallelogram originating from the same point.
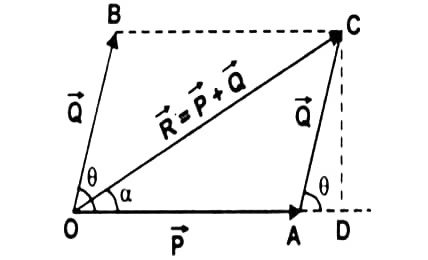
In right angled ∆COD,
OC2 = OD2 + CD2
= (OA + AD)2 + CD2
= (OA2 + AD2 + 2.OA.AD) + CD2
= P2 + Q2cos2θ + 2PQcosθ + Q2sin2θ
OC2 = P2 + Q2 + 2PQcosθ
OC = R = √(P2 + Q2 + 2PQcosθ)
Let α be the angle which the resultant R makes with P, then from ∆COD
tanα = CD/OD = CD/(OA+AD)
tanα = Qsinθ / (P + Qcosθ)
17. Derive the kinematic equations for uniformly accelerated motion.
Answer – First Equation (v = u + at) :
Acceleration is defined as the rate of change of velocity with respect to time: a = (v – u) / t
so, v = u + at
• Second Equation (s = ut + ½at2) :
Average velocity vavg = (u + v) / 2
Displacement (s) is the product of average velocity and time: s = vavg × t
Substituting v = u + at into the average velocity equation: vavg = (u + u + at) / 2 = u + ½at
Therefore, s = (u + ½at) × t = ut + ½at2
• Third Equation (v2 = u2 + 2as) :
From the first equation, t = (v – u) / a
Substitute this value of t into the second equation: s = u[(v – u) / a] + ½a [(v – u) / a]2
s = (uv – u2) / a + ½(v2 – 2uv + u2) / a
2as = 2uv – 2u2 + v2 – 2uv + u2
v2 = u2 + 2as
OR
State Newton’s Second Law of Motion. Define Work and Inertia.
Answer – Newton’s Second Law of Motion states that the rate of change of momentum of a body is directly proportional to the applied unbalanced force and takes place in the direction of the force.
If the mass is constant, it can be written as: F = ma
• Work – Work is said to be done when a force is applied on a body and the body gets displaced in the direction of the force.
W = F.d.cosθ
• Inertia – Inertia is the property of a body by virtue of which it resists any change in its state of rest or uniform motion in a straight line.
