Haryana Board (HBSE) Class 9 Maths SAT-1 Question Paper 2024 PDF Download. SAT (Student Assessment Test). HBSE Class 9 Mathematics SAT Question Paper 2024. Haryana Board Class 9 Maths Students Assessment Test 2024. HBSE Class 10th Maths SAT 2024 Answer. Haryana Board Class 9 Students Assessment Test. Haryana Board Class 9 Maths SAT Paper 2024 Solution. हरियाणा बोर्ड कक्षा 9 गणित SAT पेपर 2024.
HBSE Class 9 Maths SAT-1 Question Paper 2024 Answer Key
Instructions :
• All questions are compulsory.
• Questions (1-11) carry 1 mark each.
• Questions (12-14) carry 2 marks each.
• Questions (15-17) carry 3 marks each.
• Questions (18-19) carry 5 marks each.
• Question (20) case study, carry 4 marks.
1. निम्नलिखित में से कौन-सी संख्या एक अपरिमेय संख्या है?
Which of the following numbers is an irrational number?
(a) √16
(b) √36
(c) √48
(d) √64
Answer : (c) √48
2. 321/5 का मान है :
The value of 321/5 is :
(a) 2
(b) 32
(c) 32/5
(d) 5
Answer : (a) 2
3. 2 – x2 + x3 में x2 का गुणांक है :
The coefficient of x2 in 2 – x2 + x3 is :
(a) 1
(b) –1
(c) 2
(d) –2
Answer : (b) –1
4. निम्न में से कौन-सा p(x) = 3x + 1 का शून्यक है?
Which of the following is the zero of p(x) = 3x + 1 ?
(a) 1/3
(b) 3/2
(c) 2/3
(d) –1/3
Answer : (d) –1/3
5. दिए गए डेटा में उच्चतम और निम्नतम मानों के अंतर को कहा जाता है :
In given data the difference of highest and lowest values is called :
(a) Median
(b) Mode
(c) Range
(d) Mean
Answer : (c) Range
6. निम्नलिखित में से कौन-सा बहुपद एक रैखिक बहुपद है?
Which of the following polynomials is a linear polynomial?
(a) 1 + x
(b) y + y2 + 4
(c) x – x3
(d) y2 + y
Answer : (a) 1 + x
7. सबसे छोटी अभाज्य संख्या कौन-सी है?
Which is the smallest prime number?
Answer : 2
8. π एक परिमेय संख्या है। (सत्य / असत्य)
π is a rational number. (True / False)
Answer : False
9. 5x3 + 4x2 + 7x की घात ………… है।
The degree of 5x3 + 4x2 + 7x is …………
Answer : 3
10. वर्ग अंतराल 100-120 का वर्ग चिह्न ……….. होगा।
The Class Mark of class interval 100-120 will be ………….
Answer : 110
11. अभिकथन (A) : यदि √2 = 1.414, √3 = 1.732, तो √5 = √2 + √3.
कारण (R) : धनात्मक संख्या का वर्गमूल हमेशा मौजूद रहता है।
Assertion (A) : If √2 = 1.414, √3 = 1.732, then √5 = √2 + √3.
Reason (R) : Square root of positive number always exists.
Answer : Assertion is false but Reason is true.
12. 3 और 4 के बीच छ: परिमेय संख्याएँ ज्ञात कीजिए।
Find six rational numbers between 3 and 4.
Answer : Multiply and divide the both numbers by 7,
3 × 7/7, 4 × 7/7
21/7, 28/7
Hence, five rational numbers between 3 and 4 are 22/7, 23/7, 24/7, 25/7, 26/7, 27/7.
13. यदि x – 1, P(x) = 2x2 + kx + √2 का एक गुणनखंड है, तो k का मान ज्ञात कीजिए।
Find the value of k, if x – 1 is a factor of P(x) = 2x2 + kx + √2.
Answer : Here x – 1 = 0 so x = 1
Put x = 1 in P(x) = 2x2 + kx + √2
2(1)2 + k(1) + √2 = 0
2 + k + √2 = 0
k = – 2 – √2
k = – (2+√2)
14. 1/(√5+√2) के हर का परिमेयकरण कीजिए।
Rationalise the denominator of 1/(√5+√2).
Answer : Divide and multiply by (√5+√2)
= 1/(√5+√2) × (√5–√2)/(√5–√2)
= (√5–√2)/(√52–√22)
= (√5–√2)/(5–2) [using a2–b2 = (a–b)(a+b)]
= (√5–√2)/3
15. उपयुक्त सर्वसमिका का उपयोग करके (999)3 का मान ज्ञात करें।
Using a suitable identity, find the value of (999)3.
Answer : (999)3 = (1000 – 1)3
Using identity, (a – b)3 = a3 – b3 – 3ab(a – b)
= (1000)3 – (1)3 – 3(1000)(1)(1000–1)
= 1000000000 – 1 – 3000(999)
= 1000000000 – 1 – 299700
= 1000000000 – 299701
= 997002999
16. निम्नलिखित अवलोकनों को आरोही क्रम में व्यवस्थित किया गया है। यदि डेटा का माध्यिका 63 है, तो x का मान ज्ञात करें।
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Answer : Median = [x+(x+2)] ÷ 2 = 63
2x + 2 = 63 × 2
2x + 2 = 126
2x = 126 – 2
2x = 124
x = 124/2
x = 62
17. गुणनखंड करे : 27x3 + y3 + z3 – 9xyz
Factorize : 27x3 + y3 + z3 – 9xyz
Answer : Using identity, a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
= 27x3 + y3 + z3 – 9xyz
= (3x)3 + (y)3 + (z)3 – 3(3x)(y)(z)
= (3x + y + z)[(3x)2 + (y)2 + (z)2 – (3x)(y) – (y)(z) – (z)(3x)]
= (3x + y + 3z)(9x2 + y2 + z2 – 3xy – yz – 3zx)
18. In a mathematics test given to 15 students the following marks (out of 100) are recorded :
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
Find range, mean, median, mode.
Answer : Range = 98 – 39 = 59
Mean = 822/15 = 54.8
Ascending order of data is : 39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
Median = 8th term = 52
Mode = 52
19. एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और इसका परिमाप 540 सेमी है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
Sides of a triangle are in the ratio 12 : 17 : 25 and its perimeter is 540 cm. Find the area of the triangle.
Answer : Take, a = 12x, b = 17x, c = 25x
Perimeter (P) = a + b + c
12x + 17x + 25x = 540
54x = 540
x = 540/54 = 10
a = 12x = 12(10) = 120 cm
b = 17x = 17(10) = 170 cm
c = 25x = 25(10) = 250 cm
Semi Perimeter (s) = 540/2 = 270 cm
Using Heron’s Formula,
Area of triangle = √s(s–a)(s–b)(s–c)
A = √270(270–120)(270–170)(270–250)
= √270(150)(100)(20)
= 9000 cm2
20. केस स्टडी : IX कक्षा के एक विशेष खंड में, 40 छात्रों से उनके जन्म के महीनों के बारे में पूछा गया और प्राप्त आंकड़ों के लिए निम्नलिखित ग्राफ तैयार किया गया।
ग्राफ को देखें और निम्नलिखित प्रश्नों के उत्तर दें :
(i) नवंबर माह में कितने विद्यार्थियों का जन्म हुआ?
(ii) सबसे अधिक विद्यार्थियों का जन्म किस महीने में हुआ?
(iii) उस महीने का नाम बताइए जिसमें 4 छात्रों का जन्म हुआ।
(iv) मई से अगस्त तक जन्म लेने वाले छात्रों की कुल संख्या ज्ञात कीजिए।
CASE STUDY : In a Particular section of IX Class, 40 students were asked about the months of their birth and the following graph was prepared for the data so obtained.
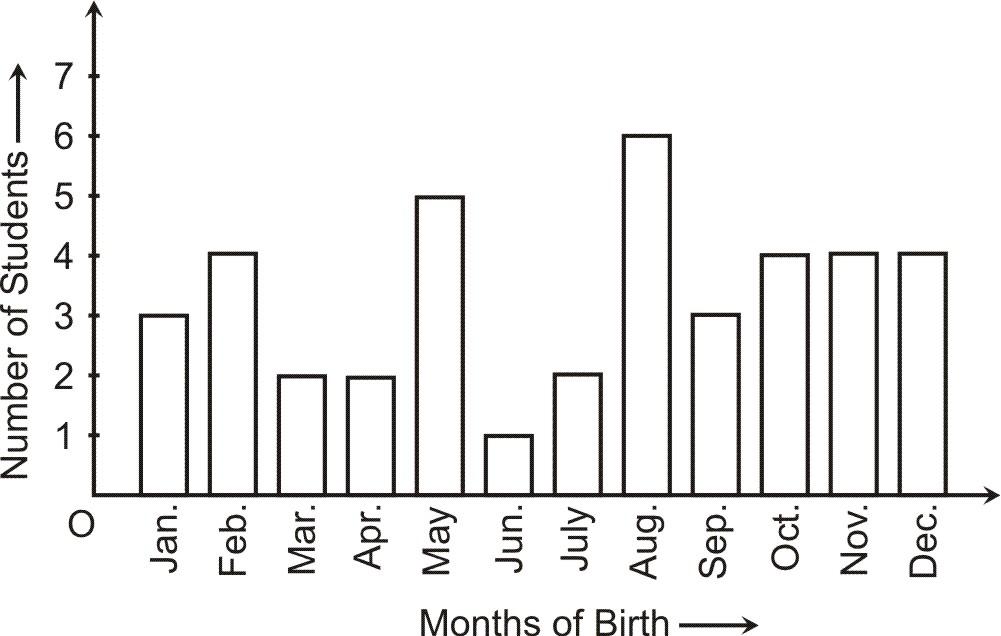
Observe the bar graph and answer the following questions :
(i) How many students were born in the month of November?
Answer : 4 students
(ii) In which month were the maximum number of students born?
Answer : August
(iii) Name the month in which 4 students were born.
Answer : Feb, Oct, Nov, Dec
(iv) Find the total number of students born from May to August.
Answer : 5 + 1 + 2 + 6 = 14 students
