Haryana Board (HBSE) Class 9 Maths Question Paper 2023 Answer Key. Haryana Board Board Solved Question Paper Class 9 Maths 2023. HBSE 9th Question Paper Download 2023. HBSE Class 9 Maths Paper Solution 2023. Haryana Board Class 9th Maths Question Paper 2023 Pdf Download with Answer. HBSE Class 9 Maths Previous Year Question Paper with Answer.
HBSE Class 9 Maths Question Paper 2023 Answer Key
1. (i) Which of the following is an irrational number ?
(A) √4/9
(B) √12/3
(C) √7
(D) √81
Answer : (C) √7
(ii) What will be the zero of the polynomial p(x) = 5x – 1 ?
(A) -1/5
(B) 1/5
(C) 4
(D) -4
Answer : (B) 1/5
Here, p(x) = 0
5x – 1 = 0
5x = 1
x = 1/5
(iii) Write the coefficient of x³ in – 3x⁴ – 7x³ + 4x + 2 :
(A) -3
(B) 3
(C) -7
(D) 4
Answer : (C) -7
(iv) Point (0, 5) lies on ………..
(A) x-axis
(B) y-axis
(C) Origin
(D) None of these
Answer : (B) y-axis
(v) How many straight lines may be drawn from any one point to any other point ?
(A) 0
(B) 1
(C) 2
(D) 3
Answer : (B) 1
(vi) A ………… is breadthless length.
(A) Point
(B) Square
(C) Rectangle
(D) Line
Answer : (D) Line
(vii) Which of the following needs a proof ?
(A) Definition
(B) Axiom
(C) Theorem
(D) Postulate
Answer : (C) Theorem
(viii) Each angle in a semicircle is a ………….
(A) Acute angle
(B) Right angle
(C) Obtuse angle
(D) Straight angle
Answer : (B) Right angle
(ix) Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is :
(A) 1 : 2
(B) 1 : 1
(C) 2 : 1
(D) 3 : 1
Answer : (B) 1 : 1
(x) Volume of the cone is :
(A) πr²h
(B) ⅔πr³
(C) 4/3πr³
(D) ⅓πr²h
Answer : (D) ⅓πr²h
(xi) The value of y is ……….. on x-axis.
(A) 1
(B) 0
(C) 2
(D) 4
Answer : (B) 0
(xii) Probability of an event lies between 0 and 1. (True / False)
Answer : True (0 ≤ P ≤ 1)
(xiii) Every rational number is an integer. (True / False)
Answer : False
(xiv) A terminated line can be produced indefinitely. (True / False )
Answer : True
(xv) A circle has only finite numbers of equal chords. (True / False)
Answer : False
(xvi) A median of a triangle divides it into two triangles of equal areas. (True / False)
Answer : True
2. Find the remainder when x³ + 3x² + 3x + 1 is divisible by x + 1.
Answer : Take x + 1 = 0 so x = -1
p(x) = x³ + 3x² + 3x + 1
p(-1) = (-1)³ + 3(-1)² + 3(-1) + 1 = – 1 + 3 – 3 +1 = 0
Remainder = 0
3. Using suitable identity, find the value of (102)².
Answer : Using Formula, (a+b)² = a² + 2ab + b²
(102)² = (100+2)² = 100² + 2(100)(2) + 2²
= 10000 + 400 + 4 = 10404
4. Find the value of ‘k’ for which x – 1 is a factor of the polynomial x² + x + k.
Answer : Here, x – 1 = 0 so x = 1
p(x) = x² + x + k
p(1) = (1)² + (1) + k = 0
1 + 1 + k = 0
k = -2
5. Find the four solutions for the equation 2x + y = 7.
Answer : There are infinite solutions of this equation y = 7 – 2x.
When x = 0, then y = 7
When x = 1, then y = 5
When x = 2, then y = 3
When x = 3, then y = 1
Four solutions are (0, 7), (1, 5), (2, 3), (3, 1)
6. Find the value of P if x = 2, y = 1 is a solution of the equation 2x + 3y = P.
Answer : 2x + 3y = P
2(2) + 3(1) = P
4 + 3 = P
P = 7
7. If ∆PRQ ≅ ∆CBA, then find :
(i) QR = ……..
Answer : AB
(ii) PR = ……..
Answer : CB
(iii) PQ = ……..
Answer : CA
(iv) ∠B = ………
Answer : ∠R
8. (i) Rationalize the denominator of 1/(√5+√2)
Answer : 1/(√5+√2)
Rationalize the denominator,
= 1/(√5+√2) × (√5-√2)/(√5-√2)
= (√5-√2)/(√5²-√2²)
= (√5-√2)/(5-2)
= (√5-√2)/3
(ii) Simplify (32)^2/5.
Answer : (2⁵)^2/5 = 2² = 4
9. Look at the above figure and answer the following :

(i) Coordinates of A, B, C, D, E
Answer : A(3, 0), B(5, 0), C(0, 3), D(-5, 0), E(0, -4)
(ii) Abscissa of point D
Answer : D(-5, 0), Abscissa (x) = -5
(iii) Ordinate of point E
Answer : E(0, -4), Ordinate = -4
(iv) Coordinates of point P, Q
Answer : P(3, 5), Q(5, -4)
10. In the given figure, AB || CD || EF and y : z = 3 : 7 are given, then find the value of x.
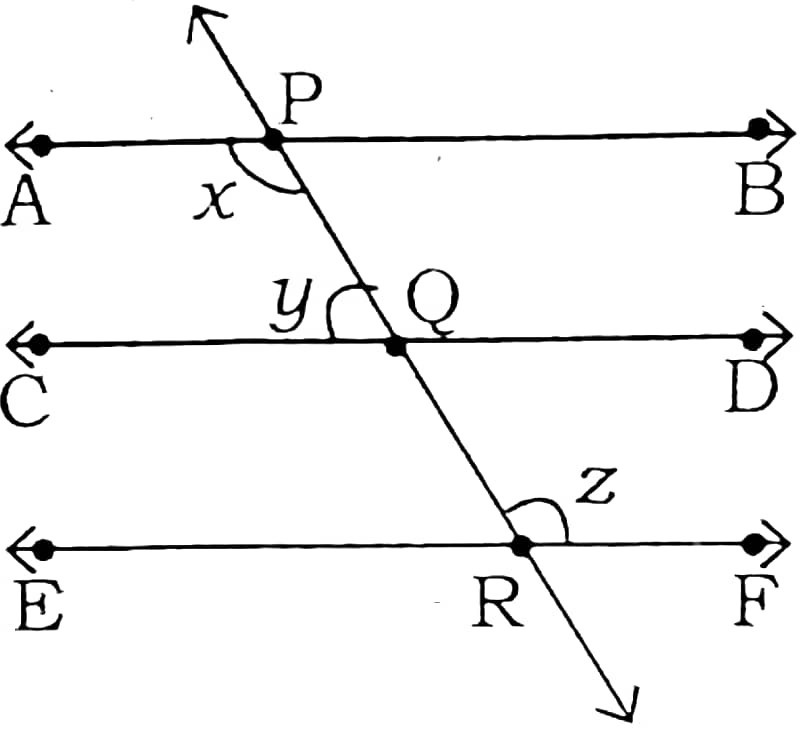
Answer : Take, y = 3a, z = 7a
y = ∠DQR (Vertical opposite angle)
∠DQR + z = 180° (Co-interior angle)
y + z = 180°
3a + 7a = 180°
10a = 180°
a = 18°
z = 7a = 7 × 18° = 126°
x = z = 126°
11. The angles of a quadrilateral are in the ratio 3 : 6 : 7 : 4. Find all the angles of the quadrilateral.
Answer : Take, angles are 3x, 6x, 7x, 4x
3x + 6x + 7x + 4x = 360°
20x = 360°
x = 360°/20 = 18°
3x = 3 × 18° = 54°
6x = 6 × 18° = 108°
7x = 7 × 18° = 126°
4x = 4 × 18° = 72°
Therefore, all angles of quadrilateral are 18°, 54°, 108° and 72°.
12. In the given figure ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
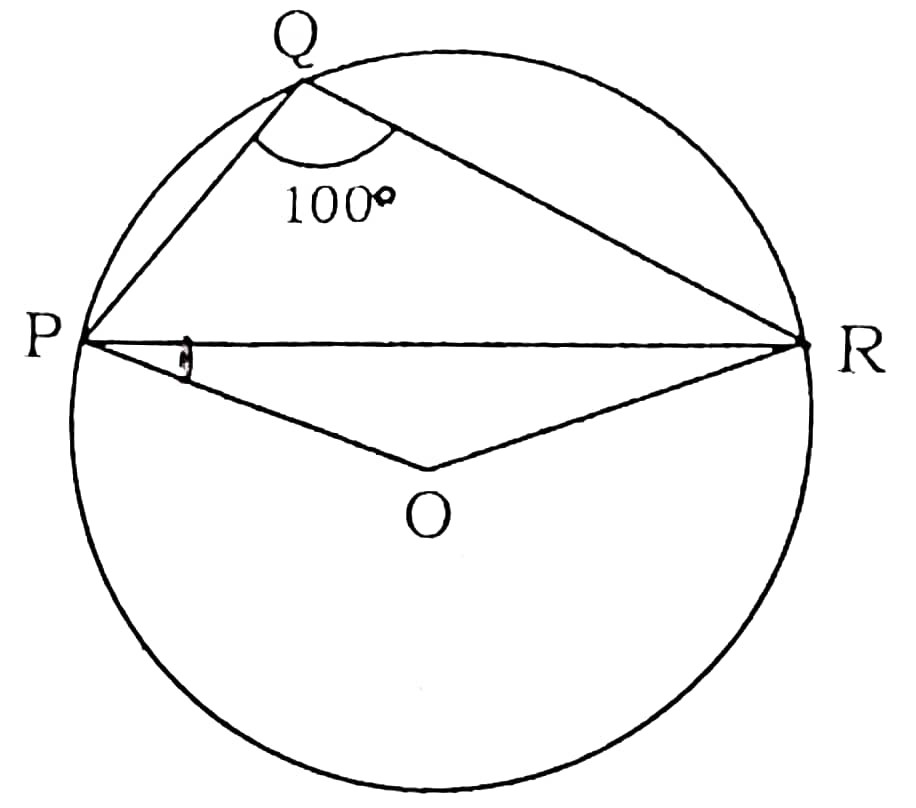
Answer : Reflex ∠POR = 2 × 100° = 200° (angle subtend at centre is double)
∠POR = 360° – 200° = 160°
∠POR + ∠OPR + ∠ORP = 180°
160° + ∠OPR + ∠OPR = 180° (Here ∠OPR = ∠ORP because PO = RO = Radius)
2∠OPR = 180° – 160° = 20°
∠OPR = 20°/2 = 10°
13. The floor of a rectangular hall has the perimeter 250 m. If the cost of the painting the four walls at the rate ₹ 12 per m² is ₹ 18000, find the height of the hall.
Answer : Perimeter of rectangle (P) = 2(L+B) = 250 m
Area of 4 walls = 2(L+B)H = 18000/12
2(L+B)H = 1500
250 × H = 1500
H = 1500/250 = 6 m
so, height of hall = 6 m
14. The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x :
29, 32, 48, 50, x, x+2, 72, 78, 84, 95
Answer : Median = [x+(x+2)] ÷ 2 = 63
2x + 2 = 63 × 2
2x + 2 = 126
2x = 126 – 2
2x = 124
x = 124/2 = 62
15. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes :

Find the probability of the following :
(i) Two heads
Answer : P(Two heads) = 72/200 = 9/25
(ii) Atmost two heads
Answer : P(Atmost two heads) = (72+77+28)/200 = 177/200
(iii) Three tails
Answer : P(Three tails or No head) = 28/200 = 7/50
16. Construct a triangle ABC in which ∠B = 60°, ∠C = 45° and perimeter is 10 cm.
Answer :
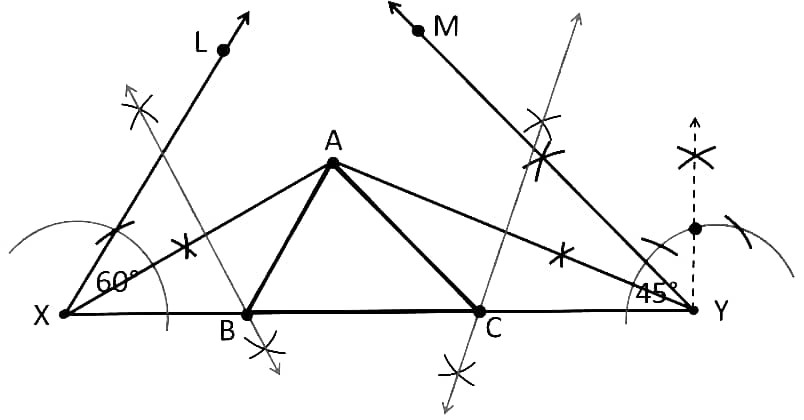
Steps of Construction :
(i) Draw a line segment XY equal to AB + BC + AC = 10 cm.
(ii) Make angle ∠LXY = 60° which is equal to ∠B = 60° .
(iii) Make angle ∠MYX = 45° which is equal to ∠C = 45°.
(iv) Bisect angles ∠LXY and ∠MYX. These bisectors intersect at a point A.
(v) Make perpendicular bisector of AX which intersect XY at point B.
(vi) Make perpendicular bisector of AY which intersect XY at point C.
(vii) Join AB & AC.
So, ∆ABC is the required triangle.
17. Sides of a triangle are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find the area of the triangle.
Answer : Take, a = 3x, b = 5x, c = 7x
Perimeter (P) = a + b + c
3x + 5x + 7x = 300
15x = 300
x = 300/15 = 20
a = 3x = 3 × 20 = 60 m
b = 5x = 5 × 20 = 100 m
c = 7x = 7 × 20 = 140 m
Semi Perimeter (s) = 300/2 = 150 m
Using Heron’s Formula,
Area of triangle = √s(s-a)(s-b)(s-c)
A = √150(150-60)(150-100)(150-140)
= √150(90)(50)(10)
= 1500√3 m²
18. A solid cube of side 12 cm cut into 8 cubes of equal volumes. Find the surface area of both the cubes.
Answer : Let side of small cube = a
8 × (Volume of small cube) = Volume of large cube
8 × a³ = 12³
8a³ = 1728
a³ = 1728/8
a³ = 216 = 6³
a = 6 cm
Surface area of large cube = 6(side)² = 6(12)² = 6(144) = 864 cm²
Surface area of small cube = 6(side)² = 6(6)² = 6(36) = 216 cm²
OR
The capacity of a closed cylindrical vessel of height 1 m is 15.4 liters. How many square meters of metal sheet would be needed to make it.
Answer : Volume or capacity of cylinder = 15.4 litres
V = 15.4 ÷ 1000 = 0.0154 m³ (1m³ = 1000 liters)
Volume of cylinder = πr²h
πr²h = 0.0154
22/7 × r² × 1 = 0.0154
r² = 0.0154 × 7/22 = 0.0049
r = √0.0049 = 0.07
Total surface area (TSA) = 2πr(r+h)
TSA = 2 × 22/7 × 0.07 × (0.07+1) = 2 × 22/7 × 0.07 × 1.07 = 0.4708 m²
Metal Sheet needed = 0.4708 m²
19. The distance (in km) of 40 Engineers from their residence to their place of work were found as follows :
5, 3, 10, 20, 25, 11, 13, 7, 12, 31, 19, 10, 12, 17, 18, 11, 32, 17, 16, 2, 7, 9, 7, 8, 3, 5, 12, 15, 18, 3, 12, 14, 2, 9, 6, 15, 15, 7, 6, 12
Construct a grouped frequency distribution table with class-size 5 for the data given above taking the first interval as 0-5 (5 not included).
Answer :
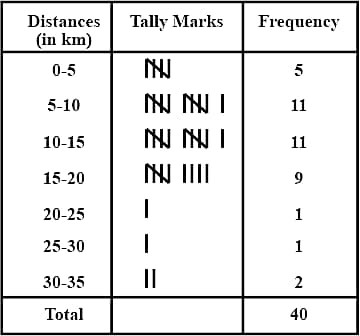
OR
A family with a monthly income of ₹6400 plans his budget for a month as given below :

(i) Represent the above data by a bar-graph.
Answer :
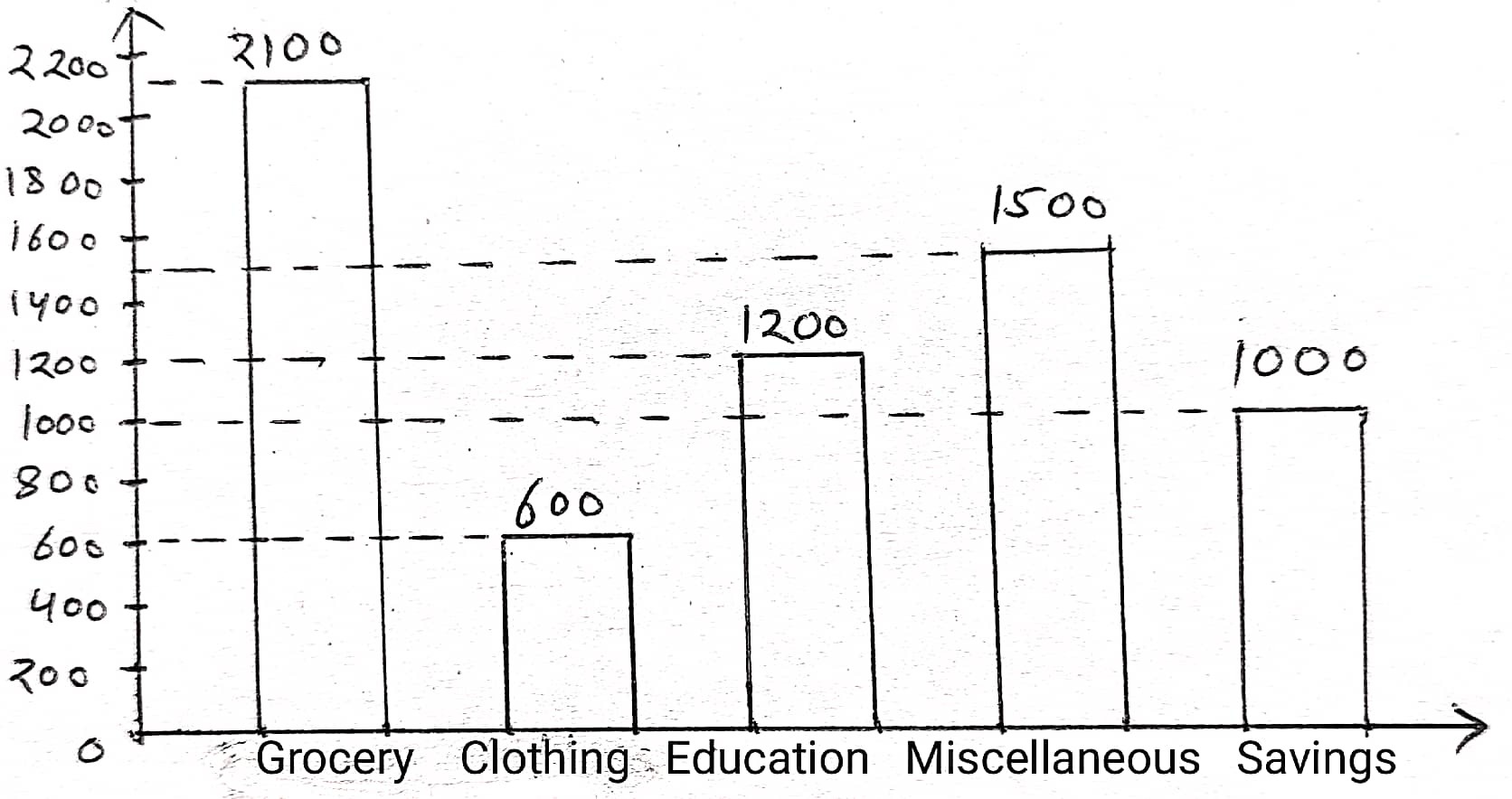
(ii) On which item they spent more ?
Answer : Grocery
