HBSE Class 10 Maths Question Paper 2023 Answer Key

Haryana Board (HBSE) Class 10 Maths Question Paper 2023 Answer Key. Haryana Board Class 10th Maths Solved Question Paper 2023 PDF Download. HBSE Board Solved Question Paper Class 10 Maths 2023. BSEH 10th Question Paper Download 2023. HBSE 10th Maths Question Paper Pdf Download 2023. HBSE 10th Class Maths Solved Question Paper 2023.

HBSE Class 10 Maths Question Paper 2023 Answer Key (All Sets – A,B,C,D)

SET–A

Q1. Which of the following is not a rational number ?
(A) √9
(B) √8
(C) √81
(D) 1.35^bar
Answer : (B) √8

Q2. If H.C.F. of 225 and 135 is 45, then their L.C.M. is :
(A) 675
(B) 1025
(C) 835
(D) 345
Answer : (A) 675
LCM × HCF = Product of two numbers
LCM = Product of two numbers ÷ HCF
LCM = (225×135) ÷ 45 = 675

Q3. The Zeroes of Polynomial 4x² – 4x + 1 are :
(A) -1/2, -1/2
(B) 1, 1/4
(C) 1/2, 1/2
(D) 1/3, 1
Answer : (C) 1/2, 1/2
4x² – 4x + 1 = 0
4x² – 2x – 2x + 1 = 0
2x(2x – 1) -1(2x – 1) = 0
(2x – 1)(2x – 1) = 0
Either 2x – 1 = 0 or 2x – 1 = 0
x = 1/2, 1/2

Q4. Which of the following is a quadratic equation ?
(A) (x – 1)(x + 3) = (x – 7)(x + 5)
(B) (2x – 1)(2x + 1) = (x – 2)²
(C) (x + 4)³ = 3x(x + 1)
(D) 4x² + 5 = (2x + 7)²
Answer : (B) (2x – 1)(2x + 1) = (x – 2)²
4x² – 1 = x² – 4x + 4
3x² + 4x – 5 = 0

Q5. Solution of a pair of linear equations x – 2y + 3 = 0 and 3x – 6y + 9 = 0 will be :
(A) Unique solution
(B) No solution
(C) Infinitely many solutions
(D) None of these
Answer : (C) Infinitely many solutions
x – 2y + 3 = 0 and 3x – 6y + 9 = 0
Here, a1 = 1, a2 = 3, b1 = -2, b2 = -6, c1 = 3, c2 = 9
a1/a2 = 1/3, b1/b2 = (-2)/(-6) = 1/3, c1/c2 = 3/9 = 1/3
a1/a2 = b1/b2 = c1/c2

Q6. The 10th term of the A.P. 3, 7, 11, 15, ……. is :
(A) 43
(B) 38
(C) -37
(D) 39
Answer : (D) 39
Here, a = 3, d = 7-3 = 4
nth term of A.P., an = a + (n-1)d
a10 = a + 9d = 3 + 9(4) = 3 + 36 = 39

Q7. If 3rd and 9th term of an A.P. are 4 and -8 respectively, then its 6th term is :
(A) -6
(B) 14
(C) -8
(D) -2
Answer : (D) -2
nth term of A.P., an = a + (n-1)d
3rd term of the A.P. = 4
a + 2d = 4 …….(i)
9th term of the A.P. = -8
a + 8d = -8 ……(ii)
Subtract eqn.(i) from eqn.(ii), we get
6d = -12
d = -2
Put d = -2 in eqn.(i),
a + 2(-2) = 4
a – 4 = 4
a = 4 + 4 = 8
so, 6th term of A.P. (a6) = a + 5d = 8 + 5(-2) = 8 – 10 = -2

Q8. In figure DE || BC. Find the length of EC.

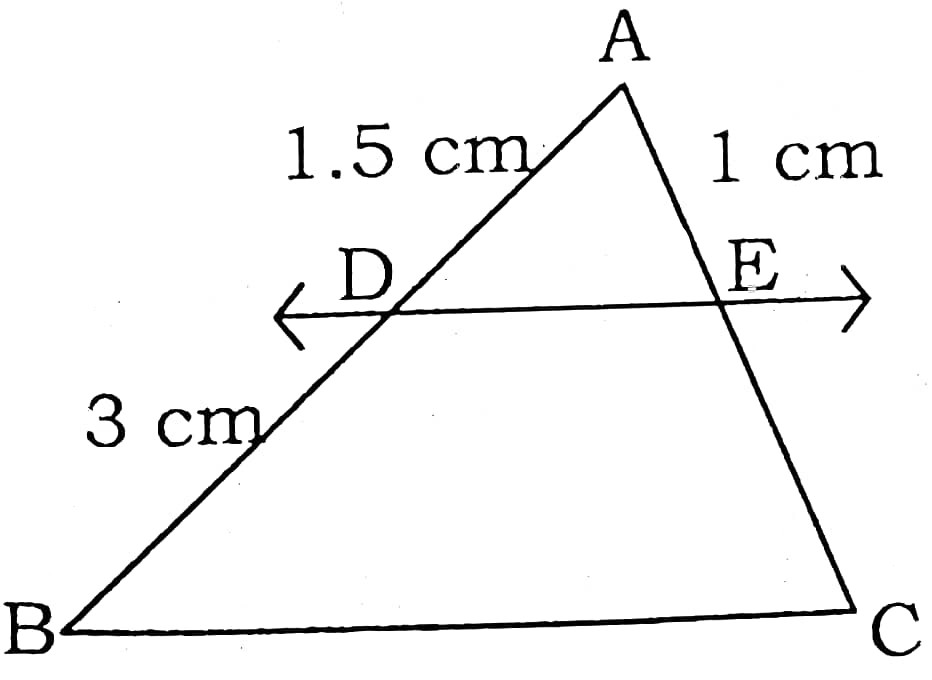
Answer :
AD/DB = AE/EC
1.5/3 = 1/EC
EC = 2 cm

Q9. If areas of two similar triangles are in the ratio 4 : 9, then ratio of their corresponding sides are :
(A) 2 : 3
(B) 16 : 81
(C) 3 : 2
(D) 4 : 9
Answer : (A) 2 : 3
If two triangles are similar to each other, then the ratio of the corresponding sides of triangles will be equal to the square root of the ratio of the corresponding areas of triangle.
so, Sides of triangles are in the ratio = √4 : √9 = 2 : 3

Q10. The distance between the points (4, 2) and (-1, -1) is :
(A) √35
(B) √34
(C) √32
(D) 6
Answer : (B) √34
Here, A(4, 2) and B(-1, -1)
x1 = 4, x2 = -1, y1 = 2, y2 = -1
Using Distance Formula,
AB = √(x2-x1)²+(y2-y1)²
= √(-1-4)²+(-1-2)²
= √(-5)²+(-3)²
= √25+9
AB = √34

Q11. The coordinates of the point which divides the line segment joining the points (4, -3) and (8, 5) in the ratio 3 : 1 internally are :
(A) (-3, 5)
(B) (4, -2)
(C) (3, 7)
(D) (7, 3)
Answer : (D) (7, 3)
Here, x1 = 4, x2 = 8, y1 = -3, y2 = 5, m1 = 3, m2 = 1
Using Section Formula,
x = (m1x2 + m2x1) ÷ (m1 + m2)
= [3(8) + 1(4)] ÷ (3 + 1)
= (24 + 4) ÷ 4 = 28 ÷ 4 = 7
y = (m1y2 + m2y1) ÷ (m1 + m2)
= [3(5) + 1(-3)] ÷ (3 + 1)
= (15 – 3) ÷ 4 = 12 ÷ 4 = 3
so, coordinates of point (x, y) = (7, 3)

Q12. The value of 9sec²A-9tan²A is :
(A) 1
(B) 8
(C) 9
(D) 0
Answer : (C) 9
Using Formula, sec²A-tan²A = 1
9sec²A-9tan²A = 9(sec²A-tan²A) = 9(1) = 9

Q13. A circle can have ………… parallel tangents at the most.
Answer : Two

Q14. Area of sector of the circle of angle θ is :
(A) πrθ/180°
(B) πr²θ/360°
(C) πrθ/360°
(D)πr²θ/90°
Answer : (B) πr²θ/360°

Q15. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then, ∠POA is equal to :
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Answer : (A) 50°

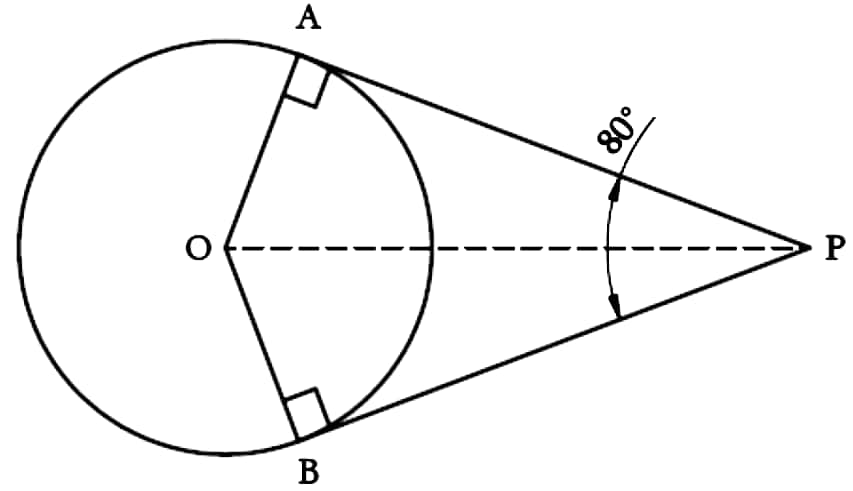
∠APO = ∠APB/2 = 80/2 = 40°
∠POA + ∠PAO + ∠APO = 180° (in ∆APO)
∠POA + 90° + 40° = 180°
∠POA + 130° = 180°
∠POA = 180° – 130° = 50°

Q16. Surface area of sphere of radius 2.1 cm is :
(A) 80.3 cm²
(B) 55.44 cm²
(C) 191.5 cm²
(D) 47.09 cm²
Answer : (B) 55.44 cm²
Surface area of sphere = 4πr² = 4 × 22/7 × 2.1 × 2.1 = 55.44 cm²

Q17. Show that 5 – √3 is an irrational number.
Solution :
Let us assume that 5 – √3 is a rational number in the form of a/b where a and b are coprime numbers and b ≠ 0.
5 – √3 = a/b
5 = a/b + √3
5 – a/b = √3
(5b-a)/b = √3
This shows (5b-a)/b is a rational number but we knows that √3 is an irrational number.
So, it contradicts our assumption and assumption of 5 – √3 is a rational number is incorrect.
Hence, it prove that 5 – √3 is a irrational.

Q18. Find the quadratic polynomial, the sum and product of whose zeroes are 1/4 and -1 respectively.
Solution :
α + β = 1/4, αβ = -1
Quadratic Polynomial = x² – (α+β)x + αβ
= x² – (1/4)x – 1
Multiple by 4, then
= 4x² – x – 4
Hence, quadratic polynomial is 4x² – x – 4.

Q19. For what value of k does the following pair of linear equations have infinite number of solutions ?
(k-1)x + (k+1)y = 3k – 1
2x + 3y = 7
Solution :
(k-1)x + (k+1)y – (3k-1) = 0 and 2x + 3y – 7 = 0
Here, a1 = k-1, a2 = 2, b1 = k+1, b2 = 3, c1 = -(3k-1), c2 = -7
a1/a2 = b1/b2 = c1/c2
(k-1)/2 = (k+1)/3 = -(3k-1)/(-7)
Take, (k-1)/2 = (k+1)/3
3(k-1) = 2(k+1)
3k – 3 = 2k + 2
3k – 2k = 2 + 3
k = 5

Q20. Find the length of the tangent from a point A which is at a distance of 5 cm from the centre of the circle of radius 3 cm.
Solution :

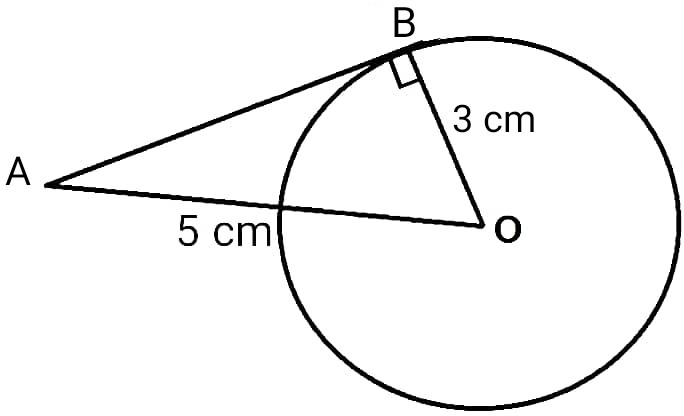
Here, AO = 5 cm, BO = 3 cm, ∠ABO = 90° (BO⊥AB)
By Pythagoras theorem in ΔABO,
Hypotenuse² = Perpendicular² + Base²
AO² = AB² + BO²
AB² = AO² – BO²
AB² = 5² – 3²
AB² = 25 – 9
AB² = 16
AB = √16
AB = 4 cm
Length of tangent (AB) = 4 cm

Q21. For what value of k the roots of the quadratic equation x² – kx + 9 = 0 are equal ?
Solution :
Here, a = 1, b = -k, c = 9
Discriminant (D) = b² – 4ac = 0
(-k)² – 4(1)(9) = 0
k² – 36 = 0
k² = 36
k = √36
k = ±6

Q22. One card is drawn from a well-shuffled deck of 52 playing cards. Find the probability of getting a red face card.
Solution :
Total cards = 52
Number of red face cards = 6
P(red face card) = Number of red face cards / Total cards = 6/52 =3/26

Q23. A fraction becomes when 1/3 when 1 is subtracted from the numerator and it becomes 1/4 when 8 is added to its denominator. Find the fraction.
Solution :
Let Numerator = x
and Denominator = y
so, Fraction = x/y
Given that, (x-1)/y = 1/3
3(x-1) = 1(y)
3x – 3 = y
3x – y = 3 …….(i)
Given that, x/(y+8) = 1/4
4(x) = 1(y+8)
4x = y + 8
4x – y = 8 …….(ii)
Subtract eqn.(i) from eqn.(ii), we get
x = 5
Put x = 5 in eqn.(i),
3(5) – y = 3
15 – y = 3
y = 12
so, Fraction = x/y = 5/12

Q24. Find the nature of roots of the following quadratic equation. If real root exist, then solve it :
2x² – 6x + 3 = 0
Solution :
Here, a = 2, b = -6, c = 3
Discriminant (D) = b² – 4ac = (-6)² – 4(2)(3) = 36 – 24 = 12 > 0
Hence, the given quadratic equation has two distinct real roots.
We know that, x = [- b ± √b²-4ac] ÷ 2a
x = [-(-6) ± √12] ÷ 2(2)
= (6 ± √12) ÷ 4
= (3±√3)/2
Roots are x = (3+√3)/2 and x = (3-√3)/2

Q25. How many three digit numbers are divisible by 7 ?
Solution :
The three-digit numbers divisible by 7 are 105, 112, 119, ……., 994
Here, a = 105, d = 112-105 = 7, last term (an) = 994
nth term of AP, an = a + (n-1)d
105 + (n-1)×7 = 994
105 + 7n – 7 = 994
7n + 98 = 994
7n = 994 – 98
7n = 896
n = 896/7
n = 128
Hence, there are 128 three-digit numbers divisible by 7.

Q26. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Solution :

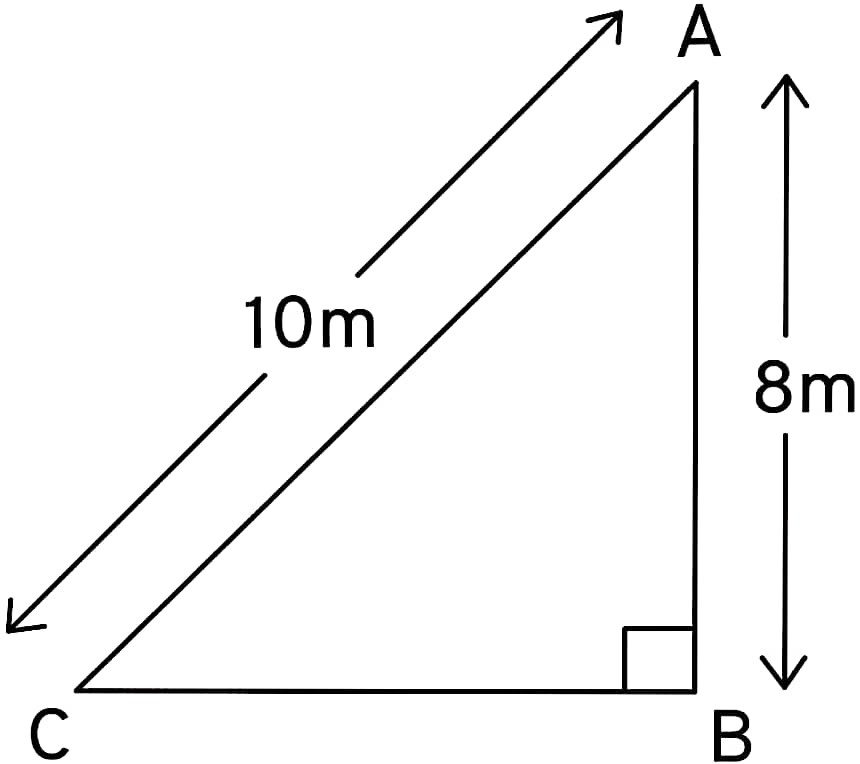
By Pythagoras theorem,
Hypotenuse² = Perpendicular² + Base²
AC² = AB² + BC²
BC² = AC² – AB²
BC² = 10² – 8²
BC² = 100 – 64
BC² = 36
BC = √36
BC = 6 m
Therefore, the distance of the foot of the ladder from the base of the wall is 6 m.

Q27. Find the value of P if the points A(2, 3), B(2, P) and C( 6, -3) are collinear.
Solution :
Area of ∆ABC = 0 (because points are collinear)
Here, x1 = 2, x2 = 2, x3 = 6, y1 = 3, y2 = P, y3 = -3
Area of triangle = ½ [x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]
½ [2(P+3) + 2(-3-3) + 6(3-P)] = 0
2P + 6 – 12 + 18 – 6P = 0
-4P +12 = 0
-4P = -12
P = 3

Q28. If A, B and C are interior angles of a triangle ABC, then show that :
sin[(B+C)/2] = cos(A/2)
Solution :
A + B + C = 180° (Angle sum property of triangle)
B + C = 180° – A
On dividing both sides by 2, we get
(B + C)/2 = (180° – A)/2
(B + C)/2 = 90° – A/2
Applying sine angles on both the sides,
sin[(B + C)/2] = sin(90° – A/2)
Since, sin(90°-θ) = cosθ, we get
sin[(B+C)/2] = cos(A/2)
Hence Proved

Q29. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding sector.
Solution :
Area of sector = θ/360 × πr² = 90/360 × 22/7 × 10 × 10 = 78.5 cm²

Q30. A die is thrown once. Find the probability of getting :
(i) a prime number
(ii) an odd number
Solution :
(i) Prime numbers = 3 (2,3,5)
Total numbers = 6 (1,2,3,4,5,6)
P(prime number) = 3/6 = 1/2
(ii) Odd numbers = 3 (1,3,5)
Total numbers = 6 (1,2,3,4,5,6)
P(odd number) = 3/6 = 1/2

Q31. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution :

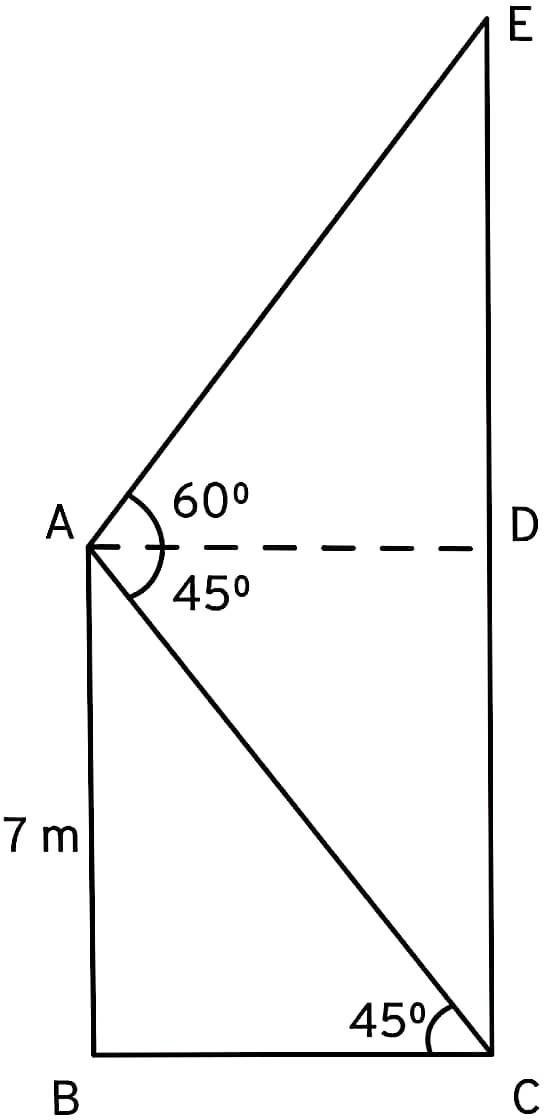
Height of building AB = 7 m and height of the tower EC = DE + CD
Also, CD = AB = 7 m and BC = AD
In right ΔABC,
tan45° = AB/BC
1 = 7/BC
BC = 7
BC = AD = 7 m
In right ∆ADE,
tan60° = DE/AD
√3 = DE/7
DE = 7√3
Height of tower EC = DE + CD = 7√3 + 7 = 7(√3+1) m

Prove that :
(1+sinθ)/cosθ + cosθ/(1+sinθ) = 2secθ
Solution :
LHS = (1+sinθ)/cosθ + cosθ/(1+sinθ)
= [(1+sinθ)²+cos²θ]/cosθ(1+sinθ)
= [1+sin²θ+2sinθ+cos²θ]/cosθ(1+sinθ)
= [1+1+2sinθ]/cosθ(1+sinθ) {using sin²θ + cos²θ = 1}
= 2(1+sinθ)/cosθ(1+sinθ)
= 2/cosθ
= 2secθ = RHS

Q32. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution :

Steps of Construction :
Step I- A circle with radius 6 cm is drawn taking O as centre.
Step II- Point P is marked at 10 cm away from centre of circle.
Step III- With the half of compass mark M which is the midpoint of OP.
Step IV- Draw a circle with centre M, taking radius MO or MP which intersects the given circle at Q and R.
Step V- Now join PQ and PR. These are the tangents of the circle.
Given radius = OQ = 6 cm and OP = 10 cm
In ∆OPQ, OQ⊥QP
Applying Pythagoras theorem we get :
OP² = OQ² + PQ²
10² = 6² + PQ²
PQ² = 100 – 36 = 64
PQ = √64 = 8 cm
PQ = PR = 8 cm
Hence, the length of tangents is 8 cm.

Q33. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution :

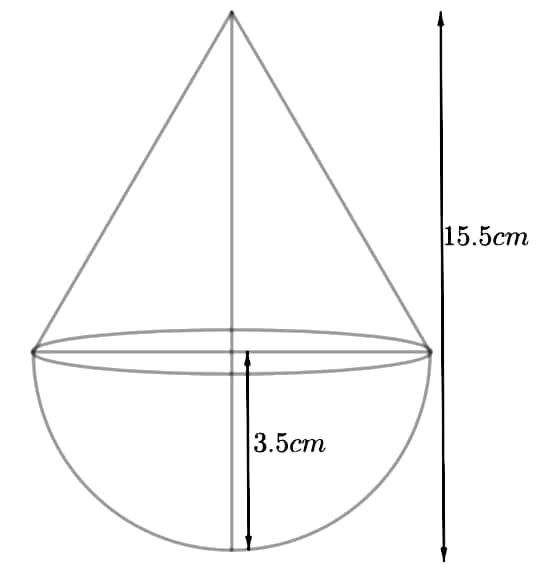
Radius of cone = radius of hemisphere = 3.5 cm
height of toy = 15.5 cm
height of cone = 15.5 – 3.5 = 12 cm
Let l be the slant height of cone,
l² = r² + h² = (3.5)² + (12)² = 12.25 + 144 = 156.25
l = √156.25 = 12.5 cm
Surface area of cone = πrl = 22/7 × 3.5 × 12.5 = 137.5 cm²
Surface area of hemisphere = 2πr² = 2 × 22/7 × 3.5 × 3.5 = 77 cm²
Total surface area of the toy = Surface area of cone + Surface area of hemisphere
Total surface area of toy = 137.5 + 77 = 214.5 cm²

A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution :
Take, radius of sphere = R, radius of cylinder = r
Volume of sphere = Volume of cylinder
4/3 × πR³ = πr²h
4/3 × 22/7 × 4.2 × 4.2 × 4.2 = 22/7 × 6 × 6 × h
h = 2.744 cm
h = 2.7 cm (approximate)

Q34. The following table gives the literacy rate (in %) of 35 cities. Find the mean literacy rate :

Solution :

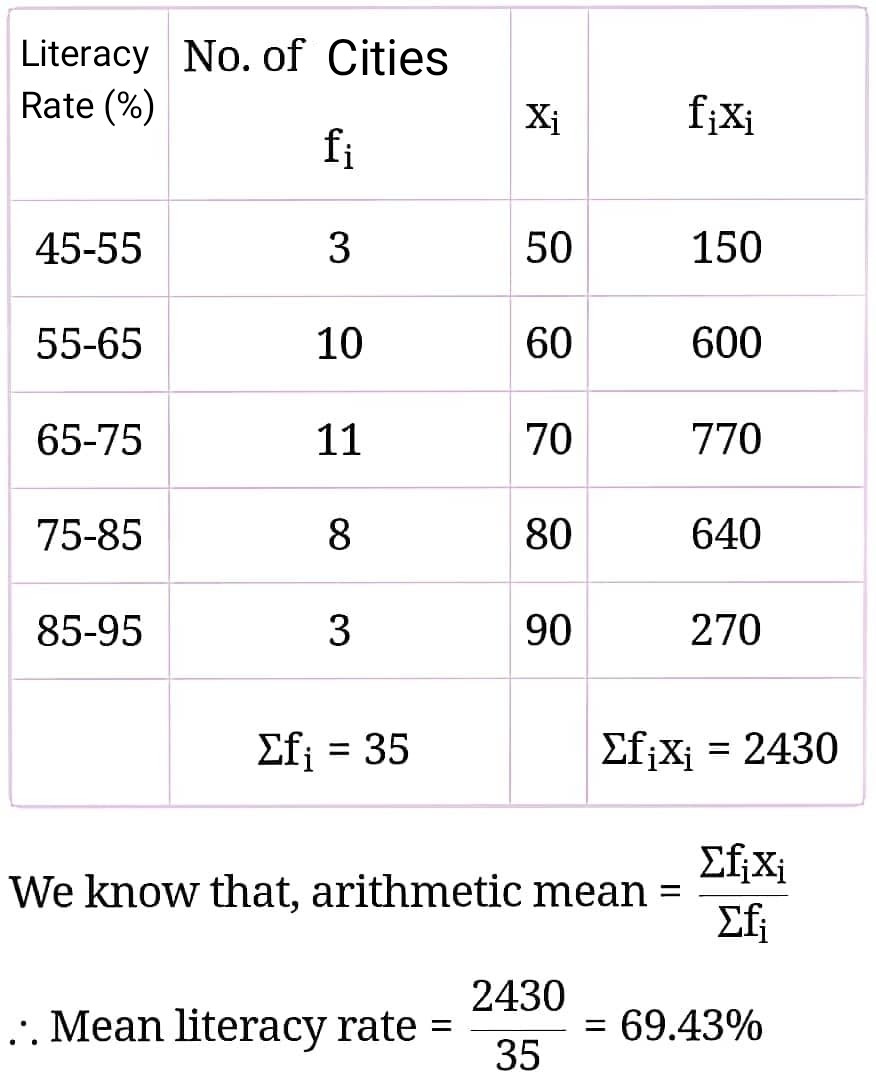
SET–B

Q1. Which of the following is not a rational number ?
(A) √16
(B) √9
(C) √10
(D) 0.35^bar
Answer : (C) √10

Q2. If H.C.F. of 26 and 91 is 13, the their L.C.M. is :
(A) 184
(B) 183
(C) 182
(D) 181
Answer : (C) 182
LCM × HCF = Product of two numbers
LCM = Product of two numbers ÷ HCF
LCM = (26×91) ÷ 13 = 182

Q3. The Zeroes of Polynomial x² + 7x + 10 are :
(A) (2, 5)
(B) (-2, -5)
(C) (-2, 5)
(D) (2, -5)
Answer : (B) (-2, -5)
x² + 7x + 10 = 0
x² + 5x + 2x + 10 = 0
x(x + 5) + 2(x + 5) = 0
(x + 5)(x + 2) = 0
Either x + 5 = 0 or x + 2 = 0
x = -5, -2

Q4. Which of the following is a quadratic equation ?
(A) (x + 1)² = 2(x – 3)
(B) (x + 4)³ = 3x(x + 1)
(C) 4x² + 5 = (2x + 7)²
(D) (x – 2)(x + 1) = (x – 1)(x + 3)
Answer : (A) (x + 1)² = 2(x – 3)
x² + 2x + 1 = 2x – 6
x² + 7 = 0

Q5. Solution of a pair of linear equations x – 2y + 5 = 0 and 3x – 6y + 10 = 0 will be :
(A) Unique solution
(B) No solution
(C) Infinitely many solutions
(D) None of these
Answer : (B) No solution
x – 2y + 5 = 0 and 3x – 6y + 10 = 0
Here, a1 = 1, a2 = 3, b1 = -2, b2 = -6, c1 = 5, c2 = 10
a1/a2 = 1/3, b1/b2 = (-2)/(-6) = 1/3, c1/c2 = 5/10 = 1/2
a1/a2 = b1/b2 ≠ c1/c2

Q6. The 10th term of the A.P. 2, 7, 12, ……. is :
(A) 40
(B) 42
(C) 45
(D) 47
Answer : (D) 47
Here, a = 2, d = 7-2 = 5
nth term of AP, an = a + (n-1)d
a10 = a + 9d = 2 + 9(5) = 2 + 45 = 47

Q7. If 3rd and 7th term of an A.P. are 5 and 9 respectively, then its 11th term is :
(A) 13
(B) 14
(C) 15
(D) 16
Answer : (A) 13
nth term of AP, an = a + (n-1)d
3rd term of the AP = 5
a + 2d = 5 …….(i)
7th term of the AP = 9
a + 6d = 9 ……(ii)
Subtract eqn.(i) from eqn.(ii), we get
4d = 4
d = 1
Put d = 1 in eqn.(i),
a + 2(1) = 5
a + 2 = 5
a = 5 – 2 = 3
so, 11th term of AP (a11) = a + 10d = 3 + 10(1) = 3 + 10 = 13

Q8. In figure DE || BC. Find the length of AD.

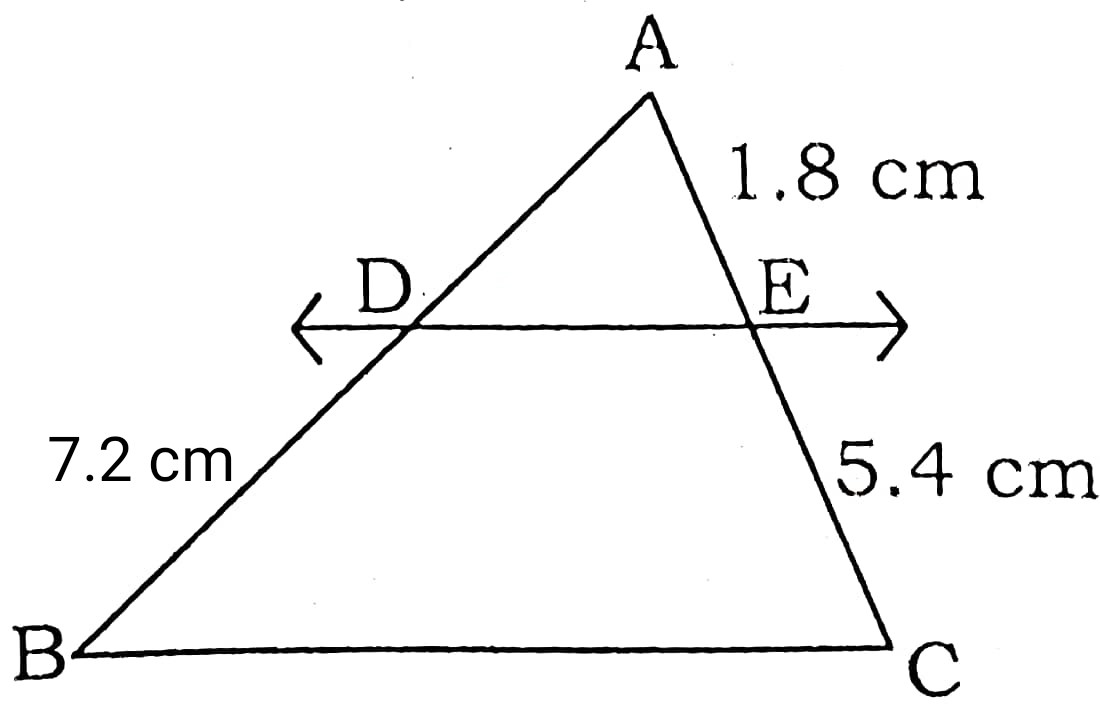
Answer :
AD/DB = AE/EC
AD/7.2 = 1.8/5.4
AD = 2.4 cm

Q9. If areas of two similar triangles are in the ratio 9 : 16, then ratio of their corresponding sides are :
(A) 81 : 256
(B) 9 : 16
(C) 3 : 4
(D) √3 : √4
Answer : (C) 3 : 4
If two triangles are similar to each other, then the ratio of the corresponding sides of triangles will be equal to the square root of the ratio of the corresponding areas of triangle.
Sides of triangles are in the ratio = √9 : √16 = 3 : 4

Q10. The distance between the points (-5, 7) and (-1, 3) is :
(A) 4√2
(B) 3√2
(C) 5√2
(D) √34
Answer : (A) 4√2
Here, A(-5, 7) and B(-1, 3)
x1 = -5, x2 = -1, y1 = 7, y2 = 3
Using Distance Formula,
AB = √(x2-x1)²+(y2-y1)²
= √(-1+5)²+(3-7)²
= √(4)²+(-4)²
= √16+16
= √32
AB = 4√2

Q11. The coordinates of the point which divides the line segment joining the points (4, -1) and (-2, -3) in the ratio 2 : 1 internally are :
(A) (0, 5/3)
(B) (-5/3, 0)
(C) (0,-7/3)
(D) (7/3, 0)
Answer : (C) (0,-7/3)
Here, x1 = 4, x2 = -2, y1 = -1, y2 = -3, m1 = 2, m2 = 1
Using Section Formula,
x = (m1x2 + m2x1) ÷ (m1 + m2)
= [2(-2) + 1(4)] ÷ (2 + 1)
= (-4 + 4) ÷ 3 = 0 ÷ 3 = 0
y = (m1y2 + m2y1) ÷ (m1 + m2)
= [2(-3) + 1(-1)] ÷ (2 + 1)
= (-6 – 1) ÷ 3 = -7 ÷ 3 = -7/3
so, coordinates of point (x, y) = (0, -7/3)

Q12. The value of 5sec²A-5tan²A is :
(A) 1
(B) 2
(C) 9
(D) 5
Answer : (D) 5
Using Formula, sec²A-tan²A = 1
5sec²A-5tan²A = 5(sec²A-tan²A) = 5(1) = 5

Q13. A line intersecting a circle in two points is called a …………..
Answer : Secant

Q14. Length of an arc of a sector of angle θ is :
(A) πrθ/180°
(B) 2πrθ/180°
(C) πrθ/360°
(D) None of these
Answer : (A) πrθ/180°
or 2πrθ/360°

Q15. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 70°, then ∠POA is equal to :
(A) 110°
(B) 55°
(C) 60°
(D) 70°
Answer : (B) 55°

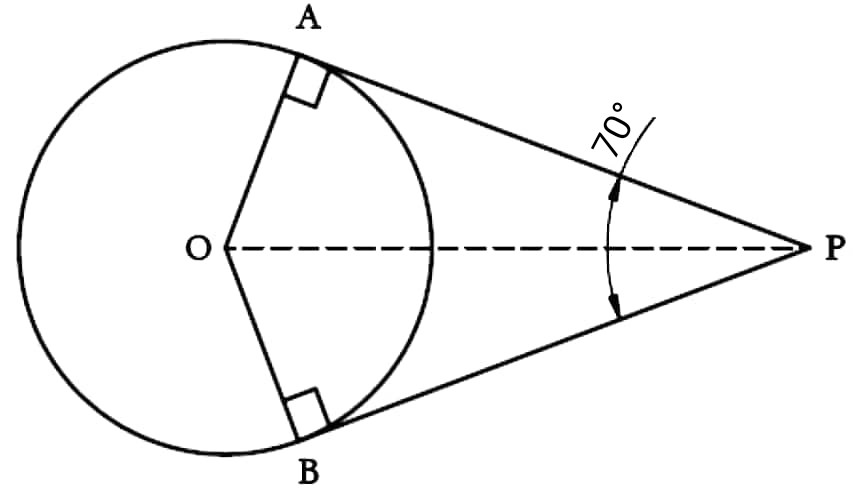
∠APO = ∠APB/2 = 70/2 = 35°
∠POA + ∠PAO + ∠APO = 180° (in ∆APO)
∠POA + 90° + 35° = 180°
∠POA + 125° = 180°
∠POA = 180° – 125° = 55°

Q16. Surface area of sphere of radius 2.8 cm is :
(A) 98.98 cm²
(B) 98.56 cm²
(C) 97.56 cm²
(D) 98.38 cm²
Answer : (B) 98.56 cm²
Surface area of sphere = 4πr² = 4 × 22/7 × 2.8 × 2.8 = 98.56 cm²

Q17. Show that 3 + √5 is an irrational number.
Solution :
Let us assume that 3 + √5 is a rational number in the form of a/b where a and b are coprime numbers and b ≠ 0.
3 + √5 = a/b
√5 = a/b – 3
√5 = (a-3b)/b
This shows (a-3b)/b is a rational number but we knows that √5 is an irrational number.
So, it contradicts our assumption and assumption of 3 + √5 is a rational number is incorrect.
Hence, it prove that 3 + √5 is a irrational.

Q18. Find the quadratic polynomial, the sum and product of whose zeroes are -1/4 and 1/4 respectively.
Solution :
α + β = -1/4, αβ = 1/4
Quadratic Polynomial = x² – (α+β)x + αβ
= x² – (-1/4)x + 1/4
= x² + (1/4)x + 1/4
Multiple by 4, then
= 4x² + x + 1
Hence, quadratic polynomial is 4x² – x + 1.

Q19. For which value of k will the following pair of linear equations have no solution ?
3x + y = 1
(2k-1)x + (k-1)y = 2k + 1
Solution :
3x + y – 1 = 0 and (2k-1)x + (k-1)y – (2k+1) = 0
Here, a1 = 3, a2 = 2k-1, b1 = 1, b2 = k-1, c1 = -1, c2 = -(2k+1) = -2k – 1
a1/a2 = b1/b2 ≠ c1/c2
3/(2k-1) = 1/(k-1) ≠ -1/(-2k-1)
Take 3/(2k-1) = 1/(k-1)
3(k-1) = 1(2k-1)
3k – 3 = 2k – 1
3k – 2k = -1 + 3
k = 2

Q20. The length of a tangent from a point A at a distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution :

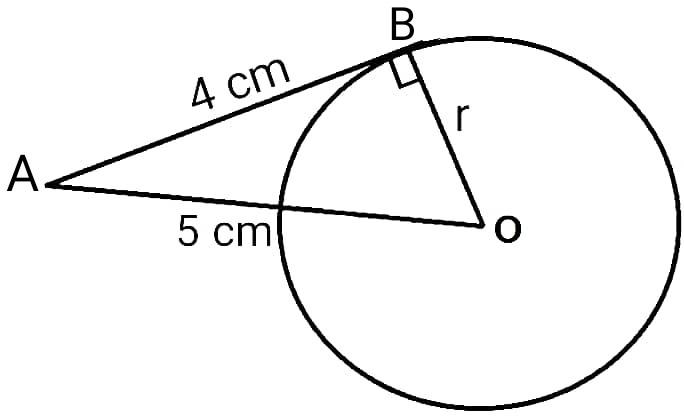
Here, AO = 5 cm, AB = 4 cm, ∠ABO = 90° (BO⊥AB)
By Pythagoras theorem in ΔABO,
Hypotenuse² = Perpendicular² + Base²
AO² = AB² + BO²
BO² = AO² – AB²
BO² = 5² – 4²
BO² = 25 – 16
BO² = 9
BO = √9
BO = 3 cm
Radius of circle (BO) = 3 cm

Q21. For what value of k the roots of the quadratic equation 2x² + kx + 3 = 0 are equal ?
Solution :
Here, a = 2, b = k, c = 3
Discriminant (D) = b² – 4ac = 0
k² – 4(2)(3) = 0
k² – 24 = 0
k² = 24
k = √24
k = ±2√6

Q22. One card is drawn from a well-shuffled deck of 52 playing cards. Find the probability of getting a King of red colour card.
Solution :
Total cards = 52
Number of King of red colour card = 2
P(king of red colour card) = Number of King of red colour card / Total cards = 2/52 =1/26

Q23. If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes 1/2 if we only add 1 to denominator. Find the fraction.
Solution :
Let Numerator = x
and Denominator = y
so, Fraction = x/y
Given that, (x+1)/(y-1) = 1
x + 1 = y – 1
x – y = -2 ……..(i)
Given that, x/(y+1) = 1/2
2(x) = y + 1
2x – y = 1 ……..(ii)
Subtract eqn.(i) from eqn.(ii), we get
x = 3
Put x = 3 in eqn.(i),
3 – y = -2
5 – y = 0
y = 5
so, Fraction = x/y = 3/5

Q24. Find the nature of roots of the following quadratic equation. If real root possible, then solve it :
9x² – 6x + 1 = 0
Solution :
Here, a = 9, b = -6, c = 1
Discriminant (D) = b² – 4ac = (-6)² – 4(9)(1) = 36 – 36 = 0
Hence, the given quadratic equation has two equal real roots.
We know that, x = [-b ± √b²-4ac] ÷ 2a
x = [-(-6) ± √0] ÷ 2(9) = (6 ± 0) ÷ 18 = 6/18 = 1/3
Roots are x = 1/3, 1/3

Q25. How many three digit numbers are divisible by 6 ?
Solution :
The three-digit numbers divisible by 6 are 102, 108, 114, …….., 996
Here, a = 102, d = 108-102 = 6, last term (an) = 994
nth term of AP, an = a + (n-1)d
102 + (n-1)×6 = 996
102 + 6n – 6 = 996
6n + 96 = 996
6n = 996 – 96
6n = 900
n = 900/6
n = 150
Hence, there are 150 three-digit numbers divisible by 6.

Q26. A wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that wire will be taut ?
Solution :

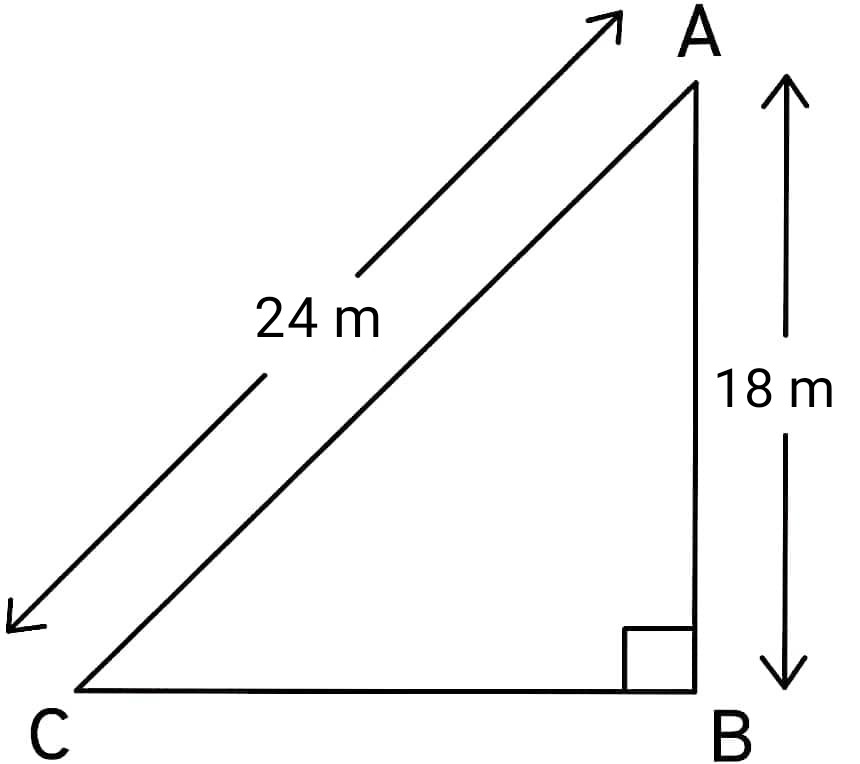
By Pythagoras theorem,
Hypotenuse² = Perpendicular² + Base²
AC² = AB² + BC²
BC² = AC² – AB²
BC² = 24² – 18²
BC² = 576 – 324
BC² = 252
BC = √252
BC = 6√7 m
Therefore, the distance of the stake from the base of pole is 6√7 m.

Q27. Find the value of R if the points A(7, -2), B(5, 1) and C(3, R) are collinear.
Solution :
Area of ∆ABC = 0 (because points are collinear)
Here, x1 = 7, x2 = 5, x3 = 3, y1 = -2, y2 = 1, y3 = R
Area of triangle = ½ [x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]
½ [7(1-R) + 5(R+2) + 3(-2-1)] = 0
7 – 7R + 5R + 10 – 9 = 0
– 2R + 8 = 0
-2R = -8
R = 4

Q28. If A, B and C are interior angles of a triangle ABC, then show that :
cos[(A+B)/2] = sin(C/2)
Solution :
A + B + C = 180° (Angle sum property of triangle)
A + B = 180° – C
On dividing both sides by 2, we get
(A + B)/2 = (180° – C)/2
(A + B)/2 = 90° – C/2
Applying cosine angles on both the sides,
cos[(A + B)/2] = cos(90° – C/2)
Since, cos(90°-θ) = sinθ, we get
cos[(A+B)/2] = sin(C/2)
Hence Proved

Q29. A chord of a circle of radius 10 cm subtends an angle of 60° at the centre. Find the area of the corresponding sector.
Solution :
Area of sector = θ/360 × πr² = 60/360 × 22/7 × 10 × 10 = 52.38 cm²

Q30. A box contain 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is :
(i) red
(ii) not red ?
Solution :
(i) Red balls = 3
Total balls = 3+5 = 8
P(red ball) = 3/8
(ii) Not red balls (means black balls) = 5
Total balls = 3+5 = 8
P(not red ball) = 5/8

Q31. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 45° and the angle of depression of its foot is also 45°. Determine the height of the tower.
Solution :

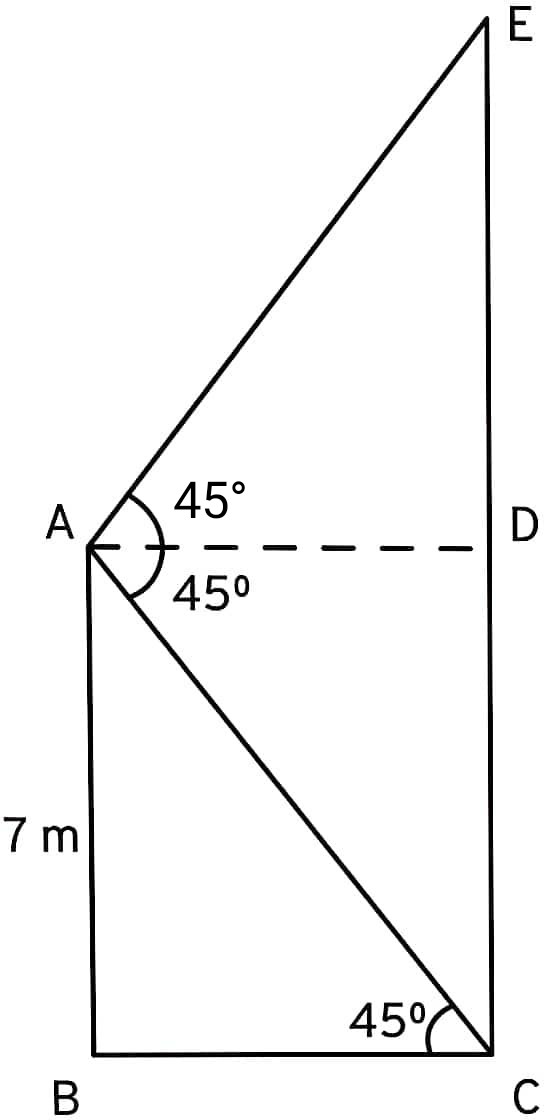
Height of building AB = 7 m and height of the tower EC = DE + CD
Also, CD = AB = 7 m and BC = AD
In right ΔABC,
tan45° = AB/BC
1 = 7/BC
BC = 7
BC = AD = 7 m
In right ∆ADE,
tan45° = DE/AD
1 = DE/7
DE = 7
Height of tower EC = DE + CD = 7 + 7 = 14 m

Prove that :
√[(1+sinA)/(1-sinA)] = secA + tanA
Solution :
LHS = √[(1+sinA)/(1-sinA)]
Rationalise the denominator,
= √[(1+sinA)/(1-sinA)] × √[(1+sinA)/(1+sinA)]
= √[(1+sinA)²/(1-sin²A)]
= √[(1+sinA)²/cos²A]
= (1+sinA)/cosA
= 1/cosA + sinA/cosA
= secA + tanA = RHS

Q32. Draw a circle of radius 5 cm. From a point 9 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution :

Steps of Construction :
Step I- A circle with radius 5 cm is drawn taking O as centre.
Step II- Point P is marked at 9 cm away from centre of circle.
Step III- With the half of compass mark M which is the midpoint of OP.
Step IV- Draw a circle with centre M, taking radius MO or MP which intersects the given circle at Q and R.
Step V- Now join PQ and PR. These are the tangents of the circle.
Given radius = OQ = 5 cm and OP = 9 cm
In ∆OPQ, OQ⊥QP
Applying Pythagoras theorem, we get :
OP² = OQ² + PQ²
9² = 5² + PQ²
PQ² = 81 – 25 = 56
PQ = √56 = 2√14 cm
PQ = PR = 2√14 cm
Hence, the length of tangents is 2√14 cm.

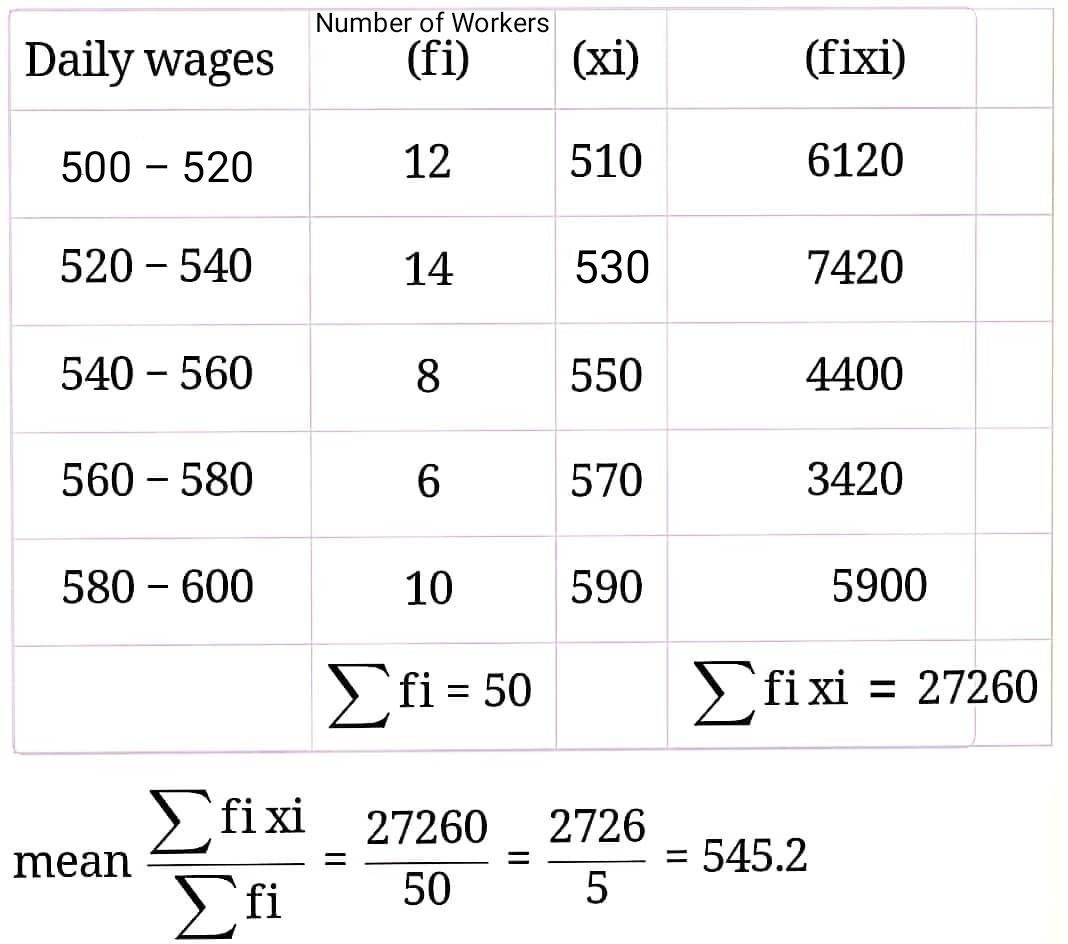
Q33. The following table gives distribution of daily wages of 50 workers of a factory. Find the mean daily wages of workers :

Solution :

Q34. A medicine capsule is in the shape of a cylinder with two hemisphere struck to each of its ends. The length of entire capsule is 14 mm and diameters of the capsule is 5 mm. Find its surface area.
Solution :

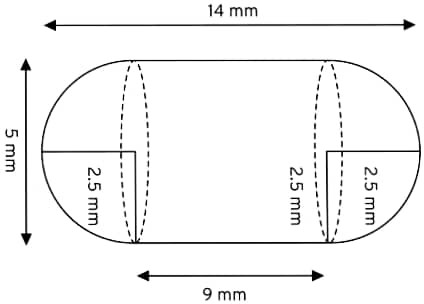
Length of capsule = 14 mm
Diameter of cylinder = 5 mm
Radius of cylinder = 5/2 mm = 2.5 mm
Diameter of hemisphere = 5 mm
Radius of hemisphere = 5/2 = 2.5 mm
Height/length of cylinder = Total length of capsule – Radius of left hemisphere – Radius of right hemisphere = 14 – 2.5 – 2.5 = 9 mm
Total Surface Area of Capsule = CSA of Cylinder + CSA of 2 Hemisphere
= 2πrh + 2×2πr²
= (2 × 22/7 × 2.5 × 9) + (2 × 2 × 22/7 × 2.5 × 2.5)
= 141.5 + 78.5
= 220 mm²
Surface area of capsule = 220 mm²

A metallic sphere of radius 3.5 cm is melted and recast into the shape of a cylinder of radius 5 cm. Find the height of the cylinder.
Solution :
Take, radius of sphere = R, radius of cylinder = r
Volume of sphere = Volume of cylinder
4/3 × πR³ = πr²h
4/3 × 22/7 × 3.5 × 3.5 × 3.5 = 22/7 × 5 × 5 × h
h = 2.3 cm (approximate)
Height of cylinder is 2.3 cm.

SET–C

Q1. Which of the following is not a rational number ?
(A) √18
(B) √16
(C) 1.25^bar
(D) √36
Answer : (A) √18

Q2. If H.C.F. of 120 and 225 is 15, then their L.C.M. is :
(A) 1600
(B) 1800
(C) 2000
(D) 2200
Answer : (B) 1800
LCM × HCF = Product of two numbers
LCM = Product of two numbers ÷ HCF
LCM = (120×225) ÷ 15 = 1800

Q3. The distance between the points (-1, -1) and (4, 2) is :
(A) √32
(B) √18
(C) 6
(D) √34
Answer : (D) √34
Here, A(-1, -1) and B(4, 2)
x1 = -1, x2 = 4, y1 = -1, y2 = 2
Using Distance Formula,
AB = √(x2-x1)²+(y2-y1)²
= √(4+1)²+(2+1)²
= √(5)²+(3)²
= √25+9
AB = √34

Q4. If corresponding sides of two similar triangles are in the ratio 3 : 4, then ratio of their areas are :
(A) √3 : 2
(B) 3 : 4
(C) 9 : 16
(D) 16 : 9
Answer : (C) 9 : 16
If two triangles are similar to each other, then the ratio of the area of triangles will be equal to the square of the ratio of the corresponding sides of triangle.
Area of triangles are in the ratio = 3² : 4² = 9 : 16

Q5. Area of sector of the circle of angle θ is :
(A) πrθ/180°
(B) πr²θ/180°
(C) πr²θ/90°
(D) πr²θ/360°
Answer : (D) πr²θ/360°

Q6. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to :
(A) 60°
(B) 50°
(C) 70°
(D) 80°
Answer : (B) 50°

∠APO = ∠APB/2 = 80/2 = 40°
∠POA + ∠PAO + ∠APO = 180° (in ∆APO)
∠POA + 90° + 40° = 180°
∠POA + 130° = 180°
∠POA = 180° – 130° = 50°

Q7. Surface area of sphere of radius 2.1 cm is :
(A) 80.3 cm²
(B) 191.5 cm²
(C) 55.44 cm²
(D) 47.09 cm²
Answer : (C) 55.44 cm²
Surface area of sphere = 4πr² = 4 × 22/7 × 2.1 × 2.1 = 55.44 cm²

Q8. A tangent to a circle intersects it in ……… point(s).
Answer : One

Q9. The value of 6sec²A-6tan²A is :
(A) 6
(B) 1
(C) 9
(D) 7
Answer : (A) 6
Using Formula, sec²A-tan²A = 1
6sec²A-6tan²A = 6(sec²A-tan²A) = 6(1) = 6

Q10. The Zeroes of Polynomial 4x² – 4x + 1 are :
(A) 1, 1/4
(B) -1/2, -1/2
(C) 1/3, 1
(D) 1/2, 1/2
Answer : (D) 1/2, 1/2
4x² – 4x + 1 = 0
4x² – 2x – 2x + 1 = 0
2x(2x – 1) -1(2x – 1) = 0
(2x – 1)(2x – 1) = 0
Either 2x – 1 = 0 or 2x – 1 = 0
x = 1/2, 1/2

Q11. Which of the following is a quadratic equation ?
(A) (x – 1)(x + 3) = (x – 7)(x + 5)
(B) (x + 4)³ = 3x(x + 1)
(C) (2x – 1)(2x + 1) = (x – 2)²
(D) 4x² + 5 = (2x + 7)²
Answer : (C) (2x – 1)(2x + 1) = (x – 2)²
4x² – 1 = x² – 4x + 4
3x² + 4x – 5 = 0

Q12. Solution of a pair of linear equations x – 2y + 3 = 0 and 3x – 6y + 9 = 0 will be :
(A) Unique solution
(B) No solution
(C) Infinitely many solutions
(D) None of these
Answer : (C) Infinitely many solutions
x – 2y + 3 = 0 and 3x – 6y + 9 = 0
Here, a1 = 1, a2 = 3, b1 = -2, b2 = -6, c1 = 3, c2 = 9
a1/a2 = 1/3, b1/b2 = (-2)/(-6) = 1/3, c1/c2 = 3/9 = 1/3
a1/a2 = b1/b2 = c1/c2

Q13. The 12th term of the A.P. 3, 7, 11, 15, …….. is :
(A) 39
(B) 49
(C) 52
(D) 47
Answer : (D) 47
Here, a = 3, d = 7-3 = 4
nth term of AP, an = a + (n-1)d
a12 = a + 11d = 3 + 11(4) = 3 + 44 = 47

Q14. If 3rd and 9th term of an A.P. 4 and -8 respectively, then its 6th term is :
(A) -6
(B) -2
(C) -8
(D) 14
Answer : (B) -2
nth term of AP, an = a + (n-1)d
3rd term of the AP = 4
a + 2d = 4 …….(i)
9th term of the AP = -8
a + 8d = -8 ……(ii)
Subtract eqn.(i) from eqn.(ii), we get
6d = -12
d = -2
Put d = -2 in eqn.(i),
a + 2(-2) = 4
a – 4 = 4
a = 4 + 4 = 8
so, 6th term of AP (a6) = a + 5d = 8 + 5(-2) = 8 – 10 = -2

Q15. In figure DE || BC. Find the length of EC.

Answer :
AD/DB = AE/EC
1.5/3 = 1/EC
EC = 2 cm

Q16. The coordinates of the point which divides the line segment joining the points (4, -3) and (8, 5) in the ratio 3 : 1 internally are :
(A) (-3, 5)
(B) (4, -2)
(C) (3, 7)
(D) (7, 3)
Answer : (D) (7, 3)
Here, x1 = 4, x2 = 8, y1 = -3, y2 = 5, m1 = 3, m2 = 1
Using Section Formula,
x = (m1x2 + m2x1) ÷ (m1 + m2)
= [3(8) + 1(4)] ÷ (3 + 1)
= (24 + 4) ÷ 4 = 28 ÷ 4 = 7
y = (m1y2 + m2y1) ÷ (m1 + m2)
= [3(5) + 1(-3)] ÷ (3 + 1)
= (15 – 3) ÷ 4 = 12 ÷ 4 = 3
so, coordinates of point (x, y) = (7, 3)

Q17. Show that 7 + √5 is an irrational number.
Solution :
Let us assume that 7 + √5 is a rational number in the form of a/b where a and b are coprime numbers and b ≠ 0.
7 + √5 = a/b
√5 = a/b – 7
√5 = (a-7b)/b
This shows (a-7b)/b is a rational number but we knows that √5 is an irrational number.
So, it contradicts our assumption and assumption of 7 + √5 is a rational number is incorrect.
Hence, it prove that 7 + √5 is a irrational.

Q18. One card is drawn from a well-shuffled deck of 52 playing cards. Find the probability of getting a red face card.
Solution :
Total cards = 52
Number of red face cards = 6
P(red face card) = Number of red face cards / Total cards = 6/52 = 3/26

Q19. For what value of k the roots of the quadratic equation x² – kx + 9 = 0 are equal ?
Solution :
Here, a = 1, b = -k, c = 9
Discriminant (D) = b² – 4ac = 0
(-k)² – 4(1)(9) = 0
k² – 36 = 0
k² = 36
k = √36
k = ±6

Q21. Find the quadratic polynomial, the sum and product of whose zeroes are 4 and 1 respectively.
Solution :
α + β = 4, αβ = 1
Quadratic Polynomial = x² – (α+β)x + αβ
= x² – 4x + 1

Q22. For what value of k does the following pair of linear equations have infinite number of solutions ?
(k-1)x + (k+1)y = 3k – 1
2x + 3y = 7
Solution :
(k-1)x + (k+1)y – (3k-1) = 0 and 2x + 3y – 7 = 0
Here, a1 = k-1, a2 = 2, b1 = k+1, b2 = 3, c1 = -(3k-1), c2 = -7
a1/a2 = b1/b2 = c1/c2
(k-1)/2 = (k+1)/3 = -(3k-1)/(-7)
Take, (k-1)/2 = (k+1)/3
3(k-1) = 2(k+1)
3k – 3 = 2k + 2
3k – 2k = 2 + 3
k = 5

Q23. If A, B and C are interior angles of a triangle ABC, then show that :
sin[(B+C)/2] = cos(A/2)
Solution :
A + B + C = 180° (Angle sum property of triangle)
B + C = 180° – A
On dividing both sides by 2, we get
(B + C)/2 = (180° – A)/2
(B + C)/2 = 90° – A/2
Applying sine angles on both the sides,
sin[(B + C)/2] = sin(90° – A/2)
Since, sin(90°-θ) = cos θ, we get
sin[(B+C)/2] = cos(A/2)
Hence Proved

Q24. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding sector.
Solution :
Area of sector = θ/360 × πr² = 90/360 × 22/7 × 10 × 10 = 78.5 cm²

Q25. A die is thrown once. Find the probability of getting :
(i) a prime number
(ii) an odd number
Solution :
(i) Prime numbers = 3 (2,3,5)
Total numbers = 6 (1,2,3,4,5,6)
P(prime numbe) = 3/6 = 1/2
(ii) Odd numbers = 3 (1,3,5)
Total numbers = 6 (1,2,3,4,5,6)
P(odd number) = 3/6 = 1/2

Q26. A fraction becomes 1/3 when 1 is subtracted from the numerator and it becomes 1/4 when 8 is added to its denominator. Find the fraction.
Solution :
Let Numerator = x
and Denominator = y
so, Fraction = x/y
Given that, (x-1)/y = 1/3
3(x-1) = 1(y)
3x – 3 = y
3x – y = 3 …….(i)
Given that, x/(y+8) = 1/4
4(x) = 1(y+8)
4x = y + 8
4x – y = 8 …….(ii)
Subtract eqn.(i) from eqn.(ii), we get
x = 5
Put x = 5 in eqn.(i),
3(5) – y = 3
15 – y = 3
y = 12
so, Fraction = x/y = 5/12

Q27. Find the nature of roots of the following quadratic equation. If real root exist, then solve it :
2x² – 6x + 3 = 0
Solution :
Here, a = 2, b = -6, c = 3
Discriminant (D) = b² – 4ac = (-6)² – 4(2)(3) = 36 – 24 = 12 > 0
Hence, the given quadratic equation has two distinct real roots.
We know that, x = [- b ± √b²-4ac] ÷ 2a
x = [-(-6) ± √12] ÷ 2(2) = (6 ± √12) ÷ 4 = (3±√3)/2
Roots are x = (3+√3)/2 and x = (3-√3)/2

Q28. How many three digit numbers are divisible by 7 ?
Solution :
The three-digit numbers divisible by 7 are 105, 112, 119, ……., 994
Here, a = 105, d = 112-105 = 7, last term (an) = 994
nth term of AP, an = a + (n-1)d
105 + (n-1)×7 = 994
105 + 7n – 7 = 994
7n + 98 = 994
7n = 994 – 98
7n = 896
n = 896/7
n = 128
Hence, there are 128 three-digit numbers divisible by 7.

Q29. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Solution :

By Pythagoras theorem,
Hypotenuse² = Perpendicular² + Base²
AC² = AB² + BC²
BC² = AC² – AB²
BC² = 10² – 8²
BC² = 100 – 64
BC² = 36
BC = √36
BC = 6 m
Therefore, the distance of the foot of the ladder from the base of the wall is 6 m.

Q30. Find the value of P if the points A(2, 3), B(2, P) and C(6, -3) are collinear.
Solution :
Area of ∆ABC = 0 (because points are collinear)
Here, x1 = 2, x2 = 2, x3 = 6, y1 = 3, y2 = P, y3 = -3
Area of triangle = ½ [x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]
½ [2(P+3) + 2(-3-3) + 6(3-P)] = 0
2P + 6 – 12 + 18 – 6P = 0
-4P +12 = 0
-4P = -12
P = 3

Q31. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution :

Radius of cone = radius of hemisphere = 3.5 cm
height of toy = 15.5 cm
height of cone = 15.5 – 3.5 = 12 cm
Let l be the slant height of cone,
l² = r² + h² = (3.5)² + (12)² = 12.25 + 144 = 156.25
l = √156.25 = 12.5 cm
Surface area of cone = πrl = 22/7 × 3.5 × 12.5 = 137.5 cm²
Surface area of hemisphere = 2πr² = 2 × 22/7 × 3.5 × 3.5 = 77 cm²
Total surface area of the toy = Surface area of cone + Surface area of hemisphere
Total surface area of toy = 137.5 + 77 = 214.5 cm²

Q32. The following table gives the literacy rate (in %) of 35 cities. Find the mean literacy rate :

Solution :

Q33. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution :

Height of building AB = 7 m and height of the tower EC = DE + CD
Also, CD = AB = 7 m and BC = AD
In right ΔABC,
tan45° = AB/BC
1 = 7/BC
BC = 7
BC = AD = 7 m
In right ∆ADE,
tan60° = DE/AD
√3 = DE/7
DE = 7√3 m
Height of tower EC = DE + CD = 7√3 + 7 = 7(√3+1)

Prove that:
(1+sinθ)/cosθ + cosθ/(1+sinθ) = 2secθ
Solution :
LHS = (1+sinθ)/cosθ + cosθ/(1+sinθ)
= [(1+sinθ)²+cos²θ]/cosθ(1+sinθ)
= [1+sin²θ+2sinθ+cos²θ]/cosθ(1+sinθ)
= [1+1+2sinθ]/cosθ(1+sinθ) {using sin²θ+cos²θ=1}
= 2(1+sinθ)/cosθ(1+sinθ)
= 2/cosθ
= 2secθ = RHS

Q34. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution :

Steps of Construction :
Step I- A circle with radius 6 cm is drawn taking O as centre.
Step II- Point P is marked at 10 cm away from centre of circle.
Step III- With the half of compass mark M which is the midpoint of OP.
Step IV- Draw a circle with centre M, taking radius MO or MP which intersects the given circle at Q and R.
Step V- Now join PQ and PR. These are the tangents of the circle.
Given radius = OQ = 6 cm and OP = 10 cm
In ∆OPQ, OQ⊥QP
Applying Pythagoras theorem, we get :
OP² = OQ² + PQ²
10² = 6² + PQ²
PQ² = 100 – 36 = 64
PQ = √64 = 8 cm
PQ = PR = 8 cm
Hence, the length of tangents is 8 cm.

SET–D

Q1. Which of the following is not a rational number ?
(A) √25
(B) √23
(C) √36
(D) 2.40^bar
Answer : (B) √23

Q2. Which of the following is a quadratic equation ?
(A) (x – 2)(x + 1) = (x – 1)(x + 3)
(B) 4x² + 5 = (2x + 7)²
(C) (x + 1)² = 2(x – 3)
(D) (x + 4)³ = 3x(x + 1)
Answer : (C) (x + 1)² = 2(x – 3)
x² + 2x + 1 = 2x – 6
x² + 7 = 0

Q3. The 10th term of the A.P. 7, 13, 19, ……….. is :
(A) 61
(B) 63
(C) 65
(D) 67
Answer : (A) 61
Here, a = 7, d = 13-7 = 6
nth term of AP, an = a + (n-1)d
a10 = a + 9d = 7 + 9(6) = 7 + 54 = 61

Q4. The Zeroes of Polynomial x² – 2x – 8 are :
(A) (2,-4)
(B) (2, 4)
(C) (-2, 4)
(D) (4, 2)
Answer : (C) (-2, 4)
x² – 2x – 8 = 0
x² – 4x + 2x – 8 = 0
x(x – 4) + 2(x – 4) = 0
(x – 4)(x + 2) = 0
Either x + 2 = 0 or x – 4 = 0
x = -2, 4

Q5. If H.C.F. of 54 and 336 is 6, then their L.C.M. is :
(A) 3021
(B) 3022
(C) 3023
(D) 3024
Answer : (D) 3024
LCM × HCF = Product of two numbers
LCM = Product of two numbers ÷ HCF
LCM = (54×336) ÷ 6 = 3024

Q6. Solution of a pair of linear equations x – 2y + 5 = 0 and 3x – 6y + 10 = 0 will be :
(A) Unique solution
(B) No solution
(C) Infinitely many solutions
(D) None of these
Answer : (B) No solution
x – 2y + 5 = 0 and 3x – 6y + 10 = 0
Here, a1 = 1, a2 = 3, b1 = -2, b2 = -6, c1 = 5, c2 = 10
a1/a2 = 1/3, b1/b2 = (-2)/(-6) = 1/3, c1/c2 = 5/10 = 1/2
a1/a2 = b1/b2 ≠ c1/c2

Q7. The value of 7sec²A-7tan²A is :
(A) 1
(B) 2
(C) 5
(D) 7
Answer : (D) 7
Using Formula, sec²A-tan²A = 1
7sec²A-7tan²A = 7(sec²A-tan²A) = 7(1) = 7

Q8. The common point of a tangent to a circle and the circle is called …………
Answer : Point of contact

Q9. Surface area of sphere of radius 2.8 cm is :
(A) 98.98 cm²
(B) 97.56 cm²
(C) 98.56 cm²
(D) 98.38 cm²
Answer : (C) 98.56 cm²
Surface area of sphere = 4πr² = 4 × 22/7 × 2.8 × 2.8 = 98.56 cm²

Q10. Length of an arc of a sector of angle θ is :
(A) πrθ/360°
(B) πrθ/180°
(C) 2πrθ/180°
(DNone of these
Answer : (B) πrθ/180°
or 2πrθ/360°

Q11. If 3rd and 7th term of an A.P. are 5 and 9 respectively, then its 11th term is :
(A) 16
(B) 15
(C) 14
(D) 13
Answer : (D) 13
nth term of AP, an = a + (n-1)d
3rd term of the AP = 5
a + 2d = 5 …….(i)
7th term of the AP = 9
a + 6d = 9 ……(ii)
Subtract eqn.(i) from eqn.(ii), we get
4d = 4
d = 1
Put d = 1 in eqn.(i),
a + 2(1) = 5
a +2 = 5
a = 5 – 2 = 3
so, 11th term of AP (a11) = a + 10d = 3 + 10(1) = 3 + 10 = 13

Q12. In figure DE || BC. Find the length of AD.

Answer :
AD/DB = AE/EC
AD/7.2 = 1.8/5.4
AD = 2.4 cm

Q13. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 60°, the ∠POA is equal to :
(A) 120°
(B) 60°
(C) 50°
(D) 70°
Answer : (B) 60°

∠APO = ∠APB/2 = 60/2 = 30°
∠POA + ∠PAO + ∠APO = 180° (in ∆APO)
∠POA + 90° + 30° = 180°
∠POA + 120° = 180°
∠POA = 180° – 120° = 60°

Q14. If corresponding sides of two similar triangles are in the ratio 4 : 9, then ratio of their areas is :
(A) 16 : 81
(B) 2 : 3
(C) 4 : 9
(D) 81 : 16
Answer : (A) 16 : 81
If two triangles are similar to each other, then the ratio of the area of triangles will be equal to the square of the ratio of the corresponding sides of triangle.
so, Areas of triangles are in the ratio = 4² : 9² = 16 : 81

Q15. The distance between the points (3, 1) and (8, 6) is :
(A) 2√2
(B) 3√2
(C) 4√2
(D) 5√2
Answer : (D) 5√2
Here, A(3, 1) and B(8, 6)
x1 = 3, x2 = 8, y1 = 1, y2 = 6
Using Distance Formula,
AB = √(x2-x1)²+(y2-y1)²
= √(8-3)²+(6-1)²
= √(5)²+(5)²
= √25+25
= √50
AB = 5√2

Q16. The coordinates of the point which divides the line segment joining the points (4, -1) and (-2, -3) in the ratio 1 : 2 internally are :
(A) (-5/3, 2)
(B) (5/3, 2)
(C) (2, -5/3)
(D) (-2, -5/3)
Answer :
Here, x1 = 4, x2 = -2, y1 = -1, y2 = -3, m1 = 1, m2 = 2
Using Section Formula,
x = (m1x2 + m2x1) ÷ (m1 + m2)
= [1(-2) + 2(4)] ÷ (1 + 2)
= (-2 + 8) ÷ 3 = 6 ÷ 3 = 2
y = (m1y2 + m2y1) ÷ (m1 + m2)
= [1(-3) + 2(-1)] ÷ (1 + 2)
= (-3 – 2) ÷ 3 = -5 ÷ 3 = -5/3
so, coordinates of point (x, y) = (2, -5/3)

Q17. Show that 4 + √5 is an irrational number.
Solution :
Let us assume that 4 + √5 is a rational number in the form of a/b where a and b are coprime numbers and b ≠ 0.
4 + √5 = a/b
√5 = a/b – 4
√5 = (a-4b)/b
This shows (a-4b)/b is a rational number but we knows that √5 is an irrational number.
So, it contradicts our assumption and assumption of 4 + √5 is a rational number is incorrect.
Hence, it prove that 4 + √5 is a irrational.

Q18. Find the quadratic polynomial, the sum and product of whose zeroes are √2 and 1/3 respectively.
Solution :
α + β = √2, αβ = 1/3
Quadratic Polynomial = x² – (α+β)x + αβ
= x² – (√2)x + 1/3
Multiple by 3, then
= 3x² – 3√2x + 1
Hence, quadratic polynomial is 3x² – 3√2x + 1.

Q19. One card is drawn from a well-shuffled deck of 52 playing cards. Find the probability of getting a king card.
Solution :
Total cards = 52
Number of King cards = 4
P(king card) = Number of King of red colour card / Total cards = 4/52 =1/13

Q20. For what value of k the roots of the quadratic equation 2x² + kx + 3 = 0 are equal ?
Solution :
Here, a = 2, b = k, c = 3
Discriminant (D) = b² – 4ac = 0
k² – 4(2)(3) = 0
k² – 24 = 0
k² = 24
k = √24
k = ±2√6

Q21. For what value of p will the following pair of linear equations have no solution ?
3x + y = 1
(2p-1)x + (p-1)y = 2p + 1
Solution :
3x + y – 1 = 0 and (2p-1)x + (p-1)y – (2p+1) = 0
Here, a1 = 3, a2 = 2p-1, b1 = 1, b2 = p-1, c1 = -1, c2 = -(2p+1) = -2p – 1
a1/a2 = b1/b2 ≠ c1/c2
3/(2p-1) = 1/(p-1) ≠ -1/(-2p-1)
Take, 3/(2p-1) = 1/(p-1)
3(p-1) = 1(2p-1)
3p – 3 = 2p – 1
3p – 2p = – 1 + 3
p = 2

Q22. The length of a tangent from a point A at a distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution :

Here, AO = 5 cm, AB = 4 cm, ∠ABO = 90° (BO⊥AB)
By Pythagoras theorem in ΔABO,
Hypotenuse² = Perpendicular² + Base²
AO² = AB² + BO²
BO² = AO² – AB²
BO² = 5² – 4²
BO² = 25 – 16
BO² = 9
BO = √9
BO = 3 cm
Radius of circle (BO) = 3 cm

Q23. How many three digit numbers are divisible by 5 ?
Solution :
The three-digit numbers divisible by 5 are 100, 105, 110, ……., 995
Here, a = 100, d = 105-100 = 5, last term (an) = 995
nth term of AP, an = a + (n-1)d
100 + (n-1)×5 = 995
100 + 5n – 5 = 995
5n + 95 = 995
5n = 995 – 95
5n = 900
n = 900/5
n = 180
Hence, there are 180 three-digit numbers divisible by 5.

Q24. A box contain 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is :
(i) red
(ii) not red ?
Solution :
(i) Red balls = 3
Total balls = 3+5 = 8
P(red ball) = 3/8
(ii) Not red balls (means black balls) = 5
Total balls = 3+5 = 8
P(not red ball) = 5/8

Q25. A chord of a circle of radius 10 cm subtends an angle of 60° at the centre. Find the area of the corresponding sector.
Solution :
Area of sector = θ/360 × πr² = 60/360 × 22/7 × 10 × 10 = 52.38 cm²

Q26. If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes 1/2 if we only add 1 to denominator. Find the fraction.
Solution :
Let Numerator = x
and Denominator = y
so, Fraction = x/y
Given that, (x+1)/(y-1) = 1
x + 1 = y – 1
x – y = -2 ……..(i)
Given that, x/(y+1) = 1/2
2(x) = y + 1
2x – y = 1 ……..(ii)
Subtract eqn.(i) from eqn.(ii), we get
x = 3
Put x = 3 in eqn.(i),
3 – y = -2
5 – y = 0
y = 5
so, Fraction = x/y = 3/5

Q27. Find the nature of roots of the following quadratic equation. If real root possible, then solve it :
9x² – 6x + 1 = 0
Solution :
Here, a = 9, b = -6, c = 1
Discriminant (D) = b² – 4ac = (-6)² – 4(9)(1) = 36 – 36 = 0
Hence, the given quadratic equation has two equal real roots.
We know that, x = [- b ± √b²-4ac] ÷ 2a
x = [-(-6) ± √0] ÷ 2(9) = (6 ± 0) ÷ 18 = 6/18 = 1/3
Roots are x = 1/3, 1/3

Q28. A wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that wire will be taut ?
Solution :

By Pythagoras theorem,
Hypotenuse² = Perpendicular² + Base²
AC² = AB² + BC²
BC² = AC² – AB²
BC² = 24² – 18²
BC² = 576 – 324
BC² = 252
BC = √252
BC = 6√7 m
Therefore, the distance of the stake from the base of pole is 6√7 m.

Q29. Find the value of x, if the points A(7, -2), B(5, 1) and C(3, x) are collinear.
Solution :
Area of ∆ABC = 0 (because points are collinear)
Here, x1 = 7, x2 = 5, x3 = 3, y1 = -2, y2 = 1, y3 = x
Area of triangle = ½ [x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]
½ [7(1-x) + 5(x+2) + 3(-2-1)] = 0
7 – 7x + 5x + 10 – 9 = 0
– 2x + 8 = 0
-2x = -8
x = 4

Q30. If A, B and C are interior angles of a triangle ABC, then show that :
cos[(A+B)/2] = sin(C/2)
Solution :
A + B + C = 180° (Angle sum property of triangle)
A + B = 180° – C
On dividing both sides by 2, we get
(A + B)/2 = (180° – C)/2
(A + B)/2 = 90° – C/2
Applying cosine angles on both the sides,
cos[(A + B)/2] = cos(90° – C/2)
Since, cos(90°-θ) = sinθ, we get
cos[(A+B)/2] = sin(C/2)
Hence Proved

Q31. A medicine capsule is in the shape of a cylinder with two hemisphere struck to each of its ends. The length of entire capsule is 14 mm and diameters of the capsule is 5 mm. Find its surface area.
Solution :

Length of capsule = 14 mm
Diameter of cylinder = 5 mm
Radius of cylinder = 5/2 mm = 2.5 mm
Diameter of hemisphere = 5 mm
Radius of hemisphere = 5/2 mm = 2.5 mm
Length/height of Cylinder = Total length of capsule – Radius of left hemisphere – Radius of right hemisphere = 14 – 2.5 – 2.5 = 9 mm
Total Surface Area of capsule = CSA of cylinder + CSA of 2 hemisphere
= 2πrh + 2×2πr²
= (2 × 22/7 × 2.5 × 9) + (2 × 2 × 22/7 × 2.5 × 2.5)
= 141.5 + 78.5
= 220 mm²
Surface area of capsule = 220 mm²

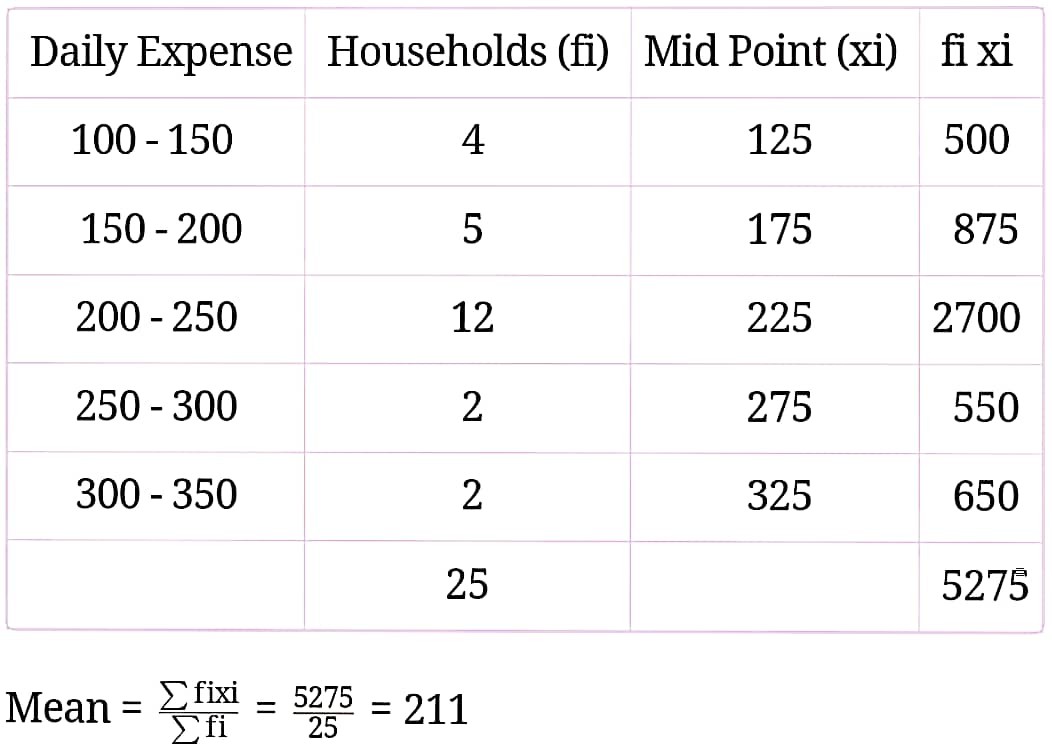
Q32. The table below shows the daily expenditure on food of 25 households in a locality. Find mean daily expenditure on food :

Solution :

Q33. Draw a circle of radius 5 cm. From a point 9 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution :

Steps of Construction :
Step I- A circle with radius 5 cm is drawn taking O as centre.
Step II- Point P is marked at 9 cm away from centre of circle.
Step III- With the half of compass mark M which is the midpoint of OP.
Step IV- Draw a circle with centre M, taking radius MO or MP which intersects the given circle at Q and R.
Step V- Now join PQ and PR. These are the tangents of the circle.
Given radius = OQ = 5 cm and OP = 9 cm
In ∆OPQ, OQ⊥QP
Applying Pythagoras theorem, we get :
OP² = OQ² + PQ²
9² = 5² + PQ²
PQ² = 81 – 25 = 56
PQ = √56 = 2√14 cm
PQ = PR = 2√14 cm
Hence, the length of tangents is 2√14 cm.

Q34. From the top of a 8 m high building, the angle of elevation of the top of a cable tower is 45° and the angle of depression of its foot is also 45°. Determine the height of the tower.
Solution :

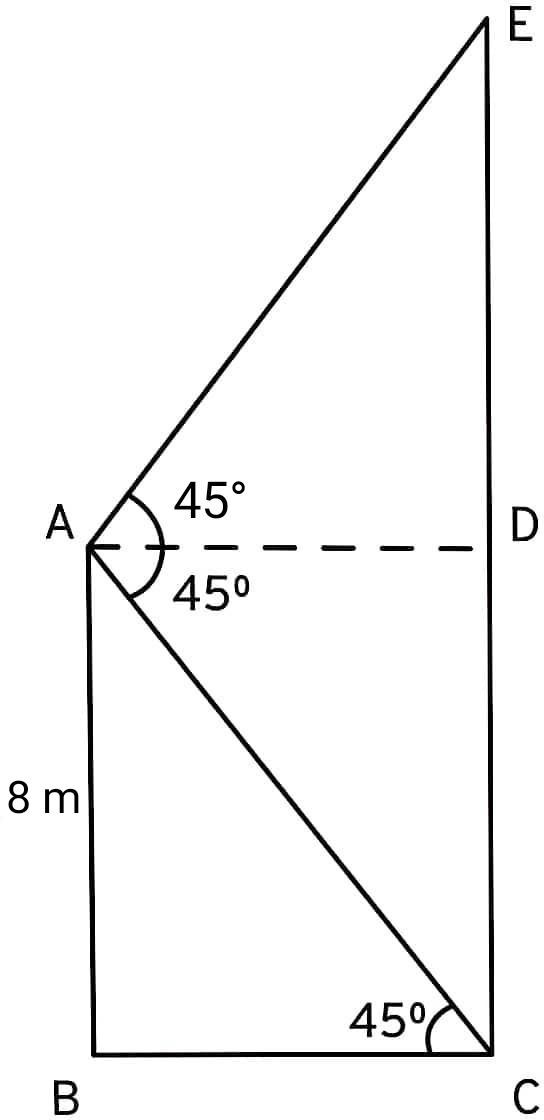
Height of building AB = 8 m and height of the tower EC = DE + CD
Also, CD = AB = 8 m and BC = AD
In right ΔABC,
tan45° = AB/BC
1 = 8/BC
BC = 8
BC = AD = 8 m
In right ∆ADE,
tan45° = DE/AD
1 = DE/8
DE = 8
Height of tower EC = DE + CD = 8 + 8 = 16 m

Leave a Comment Cancel reply