Haryana Board (HBSE) Class 9 Maths Question Paper 2025 with a fully solved answer key. Students can use this HBSE Class 9 Mathematics Solved Paper to match their responses and understand the question pattern. This BSEH Maths Answer Key 2025 is based on the latest syllabus and exam format to support accurate preparation and revision for the board exams.
HBSE Class 9 Maths Question Paper 2025 Answer Key
SECTION – A (1 Mark)
1. निम्नलिखित संख्याओं में कौन-सी परिमेय संख्या है?
(A) 1/√2
(B) 2 – √5
(C) (3 + √5) – √5
(D) 2π
उत्तर : (C) (3 + √5) – √5
Which of the following numbers is a rational number?
(A) 1/√2
(B) 2 – √5
(C) (3 + √5) – √5
(D) 2π
Answer : (C) (3 + √5) – √5
2. बहुपद 2 + x + 2x2 – 4x3 की घात क्या है?
(A) 2
(B) 3
(C) 4
(D) 1
उत्तर : (B) 3
What is the degree of the polynomial 2 + x + 2x2 – 4x3?
(A) 2
(B) 3
(C) 4
(D) 1
Answer : (B) 3
3. रिक्त स्थान भरें :
(x + y)(x – y) = ………
उत्तर : x2 – y2
Fill in the blank :
(x + y)(x – y) = ………
Answer : x2 – y2
4. निम्न में से कौन-सा त्रिभुजों की सर्वांगसमता की कसौटी नहीं है?
(A) SAS
(B) ASA
(C) SSA
(D) SSS
उत्तर : (C) SSA
Which of the following is not a criterion for congruence of triangles?
(A) SAS
(B) ASA
(C) SSA
(D) SSS
Answer : (C) SSA
5. एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण …………… होते हैं।
उत्तर : बराबर
Angles opposite to equal sides of an isosceles triangle are …………..
Answer : equal
6. समीकरण –2x + 3y = 6 को ax + by + c = 0 के रूप में व्यक्त कीजिए और b का मान बताइए :
(A) –3
(B) 3
(C) 2
(D) –2
उत्तर : (B) 3
Express –2x + 3y = 6 as ax + by + c = 0 and write the the value of b :
(A) –3
(B) 3
(C) 2
(D) –2
Answer : (B) 3
7. ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है, तो ∠B और ∠C का मान होगा :
(A) प्रत्येक 45°
(B) 35°, 45°
(C) 30°, 50°
(D) 50°, 40°
उत्तर : (A) प्रत्येक 45°
∠B = ∠C (क्योंकि AB = AC)
∠A + ∠B + ∠C = 180° (त्रिभुज के सभी कोणों का योग 180°)
90° + ∠B + ∠B = 180°
2∠B = 180° – 90°
∠B = 90°/2 = 45°
∠B = ∠C = 45°
If ABC is a right triangle, where ∠A = 90° and AB = AC, then find the value of ∠B and ∠C :
(A) Each 45°
(B) 35°, 45°
(C) 30°, 50°
(D) 50°, 40°
Answer : (A) Each 45°
∠B = ∠C (because AB = AC)
∠A + ∠B + ∠C = 180° (sum of all angles of a triangle is 180°)
90° + ∠B + ∠B = 180°
2∠B = 180° – 90°
∠B = 90°/2 = 45°
∠B = ∠C = 45°
8. एक लंबवृत्तीय शंकु का आयतन होगा यदि इसकी त्रिज्या 6 cm और ऊँचाई 7 cm हो :
(A) 264 cm3
(B) 246 cm2
(C) 120 cm2
(D) 420 cm2
उत्तर : (A) 264 cm3
लंबवृत्तीय शंकु का आयतन = 1/3πr2h
= 1/3 × 22/7 × (6)2 × 7 = 264 cm3
The volume of a right circular cone will be if its radius is 6 cm and height is 7 cm :
(A) 264 cm3
(B) 246 cm2
(C) 120 cm2
(D) 420 cm2
Answer : (A) 264 cm3
Volume of a right circular cone = 1/3πr2h
= 1/3 × 22/7 × (6)2 × 7 = 264 cm3
9. चक्रीय चतुर्भुज के सम्मुख कोणों के एक युग्म का योग होता है :
(A) 180°
(B) 150°
(C) 90°
(D) 60°
उत्तर : (A) 180°
The sum of the pair of opposite angles of a cyclic quadrilateral is :
(A) 180°
(B) 150°
(C) 90°
(D) 60°
Answer : (A) 180°
10. गोले का पृष्ठीय क्षेत्रफल होगा :
(Α) 4/3πr3
(Β) 4πr2
(C) 4πr3
(D) 3πr2
उत्तर : (Β) 4πr2
The surface area of a sphere will be :
(Α) 4/3πr3
(Β) 4πr2
(C) 4πr3
(D) 3πr2
Answer : (Β) 4πr2
11. किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य बिंदुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समांतर होता है और उसका …………. होता है।
(A) दो गुना
(B) आधा
(C) तीन गुना
(D) इनमें से कोई नहीं
उत्तर : (B) आधा
The line segment joining the mid points of any two sides of a triangle is parallel to the third side and is …………. of it.
(A) double
(B) half
(C) three times
(D) None of these
Answer : (B) half
12. आकृति में, ∠ABC = 69° और ∠ACB =31° हो, तो ∠BDC होगा :
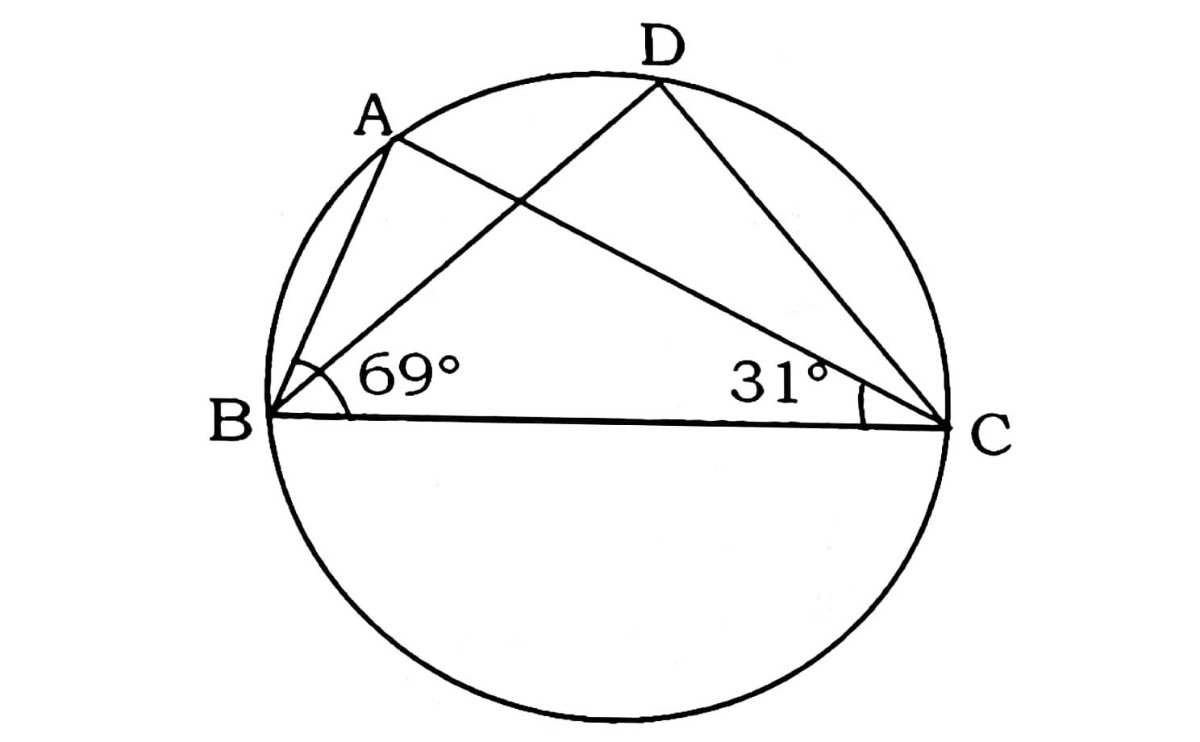
उत्तर : In ∆ABC,
∠ABC + ∠ACB + ∠BAC = 180° (त्रिभुज के सभी कोणों का योग 180° होता हैं)
69° + 31° + ∠BAC = 180°
∠BAC = 180° – 100° = 80°
∠BDC = ∠BAC (वृत्त के एक ही खंड में बने कोण बराबर होते हैं)
इसलिए, ∠BDC = 80°
In fig., ∠ABC = 69° and ∠ACB = 31°, ∠BDC will be :

Answer : In ∆ABC,
∠ABC + ∠ACB + ∠BAC = 180° (sum of all angles of a triangle is 180°)
69° + 31° + ∠BAC = 180°
∠BAC = 180° – 100° = 80°
∠BDC = ∠BAC (angles in the same segment of a circle are equal)
so, ∠BDC = 80°
13. एक त्रिभुज का आधार व ऊँचाई क्रमशः 10 cm व 6 cm है। उसका क्षेत्रफल होगा :
(A) 40 cm2
(B) 35 cm2
(C) 30 cm2
(D) 15 cm2
उत्तर : (C) 30 cm2
त्रिभुज का क्षेत्रफल = 1/2 × आधार × ऊँचाई
= 1/2 × 10 × 6 = 30 cm2
The base and height of a triangle are 10 cm and 6 cm respectively. Its area will be :
(A) 40 cm2
(B) 35 cm2
(C) 30 cm2
(D) 15 cm2
Answer : (C) 30 cm2
Area of triangle = 1/2 × base × height
= 1/2 × 10 × 6 = 30 cm2
14. आयत के विकर्ण परस्पर समद्विभाजित करते हैं और बराबर होते हैं। (सत्य / असत्य)
उत्तर : सत्य
The diagonals of a rectangle bisects each other and equal. (True / False)
Answer : True
15. यदि एक चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करें, तो वह एक ………….. होता है।
उत्तर : समांतर चतुर्भुज
If the diagonals of a quadrilateral bisect each other, then it is a …………..
Answer : parallelogram
16. आकृति में, रेखाएँ PQ और RS परस्पर बिंदु पर O प्रतिच्छेद करती हैं। यदि ∠POR = 60° है, तो ∠SOQ होगा :

(A) 120°
(B) 90°
(C) 60°
(D) 30°
उत्तर : (C) 60° (ऊर्ध्वाधर विपरीत कोण)
In fig., lines PQ and RS intersect each other at point O. If ∠POR = 60°, then ∠SOQ will be :

(A) 120°
(B) 90°
(C) 60°
(D) 30°
Answer : (C) 60° (vertical opposite angle)
17. बारंबारता बंटन का एक आयत चित्र खींचने के लिए वर्ग 30-40 की समायोजित बारंबारता है :
| वर्ग अंतराल | 0-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-100 |
| बारंबारता | 7 | 10 | 10 | 20 | 20 | 15 | 8 |
(A) 10
(B) 15
(C) 20
(D) 3.5
उत्तर : (A) 10
समायोजित बारंबारता = (न्यूनतम चौड़ाई / वर्ग चौड़ाई) × बारंबारता = 10/10 × 10 = 10
To draw a histogram to represent the following frequency distribution. The adjusted frequency for the class-interval 30-40 is :
| Class Interval | 0-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-100 |
| Frequency | 7 | 10 | 10 | 20 | 20 | 15 | 8 |
(A) 10
(B) 15
(C) 20
(D) 3.5
Answer : (A) 10
Adjusted frequency = (minimum width / class width) × frequency = 10/10 × 10 = 10
18. वर्ग अंतराल 150-160 का वर्ग चिह्न है :
(A) 150
(B) 155
(C) 160
(D) 310
उत्तर : (B) 155
वर्ग चिह्न = (निम्न सीमा + उच्च सीमा) / 2 = (150 + 160) / 2 = 310/2 = 155
The class mark of the class interval 150-160 is :
(A) 150
(B) 155
(C) 160
(D) 310
Answer : (B) 155
Class mark = (lower limit + upper limit) / 2 = (150 + 160) / 2 = 310/2 = 155
19. अभिकथन (A) : यदि √2 = 1.414, √3 = √1.732 है, तब √5 = √2 + √3.
तर्क (R) : धनात्मक संख्या का वर्गमूल हमेशा मौजूद रहता है।
(A) (A) और (R) दोनों सत्य हैं और (R), (A) की सही व्याख्या है।
(B) (A) और (R) दोनों सत्य हैं और (R), (A) की सही व्याख्या नहीं है।
(C) (A) सत्य है लेकिन (R) असत्य है।
(D) (A) असत्य है लेकिन (R) सत्य है।
उत्तर : (D) (A) असत्य है लेकिन (R) सत्य है।
(अभिकथन असत्य है क्योंकि √5 ≠ √2 + √3)
Assertion (A) : If √2 = 1.414, √3 = √1.732, then √5 = √2 + √3.
Reason (R) : The square root of every positive number always exists.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true, but (R) is not correct explanation of (A).
(C) (A) is true, but (R) is false.
(D) (A) is false, but (R) is true.
Answer : (D) (A) is false, but (R) is true.
(assertion is false because √5 ≠ √2 + √3)
20. अभिकथन (A) : एक वृत्त में समान जीवाओं की अनंत संख्या हो सकती है।
तर्क (R) : एक वृत्त में समान जीवाओं की केवल सीमित संख्या होती है।
(A) (A) और (R) दोनों सत्य हैं और (R), (A) की सही व्याख्या है।
(B) (A) और (R) दोनों सत्य हैं लेकिन (R), (A) की सही व्याख्या नहीं है।
(C) (A) सत्य है लेकिन (R) असत्य है।
(D) (A) असत्य है लेकिन (R) सत्य है।
उत्तर : (C) (A) सत्य है लेकिन (R) असत्य है।
(तर्क असत्य है क्योंकि एक वृत्त में अनंत बराबर जीवाएँ होती हैं)
Assertion (A) : A circle can have infinite equal chords.
Reason (R) : A circle has only limited equal chords.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true, but (R) is not correct explanation of (A).
(C) (A) is true, but (R) is false.
(D) (A) is false, but (R) is true.
Answer : (C) (A) is true, but (R) is false.
(reason is false because a circle has infinite equal chords)
SECTION – B (2 Marks)
21. 0.6 (बार) को p/q के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।
उत्तर : मान लीजिए x = 0.666… (i)
दोनों पक्षों को 10 से गुणा करने पर,
10x = 6.666… (ii)
समीकरण (i) को (ii) में से घटाने पर,
10x – x = 6.666… – 0.666…
9x = 6
x = 6/9 = 2/3
Express 0.6 (bar) in the form of p/q where p and q are two integers and q ≠ 0.
Answer : Let x = 0.666… (i)
Multiply both sides by 10,
10x = 6.666… (ii)
Subtract eqn.(i) from (ii), we get
10x – x = 6.666… – 0.666…
9x = 6
x = 6/9 = 2/3
22. 1/(2 + √3) के हर का परिमेयकरण कीजिए।
उत्तर : अंश और हर को (2 – √3) से गुणा करें,
= 1/(2 + √3) × (2 – √3)/(√2 – √3)
सर्वसमिका का प्रयोग, (a – b)(a + b) = a2 – b2
= (2 – √3)/(22 – √32)
= (2 – √3)/(4 – 3)
= (2 – √3)/1
= 2 – √3
Rationalize the denominator of 1/(2 + √3).
Answer : Multiply the numerator and denominator by (2 – √3),
= 1/(2 + √3) × (2 – √3)/(√2 – √3)
Using the identity, (a – b)(a + b) = a2 – b2
= (2 – √3)/(22 – √32)
= (2 – √3)/(4 – 3)
= (2 – √3)/1
= 2 – √3
OR
सरल कीजिए : (√3 + √7)(√3 + √7)
उत्तर : (√3 + √7)(√3 + √7) = (√3 + √7)2
सर्वसमिका का प्रयोग, (a + b)2 = a2 + b2 + 2ab
(√3 + √7)2 = (√3)2 + (√7)2 + 2(√3)(√7)
= 3 + 7 + 2√21
= 10 + 2√21
Simplify : (√3 + √7)(√3 + √7)
Answer : (√3 + √7)(√3 + √7) = (√3 + √7)2
Using the identity, (a + b)2 = a2 + b2 + 2ab
(√3 + √7)2 = (√3)2 + (√7)2 + 2(√3)(√7)
= 3 + 7 + 2√21
= 10 + 2√21
23. k का मान ज्ञात कीजिए, यदि (x – 1), P(x) का गुणनखण्ड है P(x) = kx2 – 3x + k.
उत्तर : यहाँ x – 1 = 0
x = 1 को P(x) = kx2 – 3x + k में रखने पर
k(1)2 – 3(1) + k = 0
k – 3 + k = 0
2k = 3
k = 3/2
Find the value of k, if (x – 1) is a factor of P(x), P(x) = kx2 – 3x + k.
Answer : Here x – 1 = 0
Put x = 1 in P(x) = kx2 – 3x + k
k(1)2 – 3(1) + k = 0
k – 3 + k = 0
2k = 3
k = 3/2
OR
सीधे गुणा किए बिना 105 × 106 का मान ज्ञात कीजिए।
उत्तर : 105 × 106 = (100 + 5)(100 + 6)
सर्वसमिका का प्रयोग, (x + a)(x + b) = x2 + (a + b)x + ab
= (100)2 + (5 + 6)100 + (5 × 6)
= 10000 + 1100 + 30
= 11130
Evaluate 105 × 106 without directly multiplying.
Answer : 105 × 106 = (100 + 5)(100 + 6)
Using the identity, (x + a)(x + b) = x2 + (a + b)x + ab
= (100)2 + (5 + 6)100 + (5 × 6)
= 10000 + 1100 + 30
= 11130
24. k का मान ज्ञात कीजिए, यदि x = 2, y = 1 समीकरण 2x + 3y = k का एक हल हो।
उत्तर : दिए गए मानों x और y को समीकरण 2x + 3y = k में स्थापित करने पर,
2(2) + 3(1) = k
4 + 3 = k
k = 7
Find the value of k, if x = 2, y = 1 are the solution of 2x + 3y = k.
Answer : Substitute the given values of x and y in 2x + 3y = k.
2(2) + 3(1) = k
4 + 3 = k
k = 7
25. यूक्लिड की पहली व दूसरी अभिधारणा लिखिए।
उत्तर : यूक्लिड का पहला अभिधारणा : किसी भी बिंदु से किसी भी दूसरे बिंदु तक एक सीधी रेखा खींची जा सकती है।
यूक्लिड का दूसरा अभिधारणा : एक सीमित रेखा को अनंत तक बढ़ाया जा सकता है।
Write first and second postulates of Euclid.
Answer : Euclid’s First Postulate: A straight line may be drawn from any one point to any other point.
Euclid’s Second Postulate: A terminated line can be produced indefinitely.
SECTION – C (3 Marks)
26. समीकरण 2x + y = 7 के तीन हल ज्ञात कीजिए।
उत्तर : समीकरण 2x + y = 7 के अनंत हल हैं।
y = 7 – 2x
x = 0 लेने पर y = 7 – 2(0) = 7
x = 1 लेने पर y = 7 – 2(1) = 5
x = 2 लेने पर y = 7 – 2(2) = 3
अतः (0, 7), (1, 5) और (2, 3) दिए गए समीकरण के तीन हल हैं।
Find three solutions of equation 2x + y = 7.
Answer : There are infinite solutions of given equation 2x + y = 7.
y = 7 – 2x
Taking x = 0 then y = 7 – 2(0) = 7
Taking x = 1 then y = 7 – 2(1) = 5
Taking x = 2 then y = 7 – 2(2) = 3
Hence (0, 7), (1, 5) and (2, 3) are three solutions of the given equation.
27. 1/7 और 2/7 के बीच की तीन अपरिमेय संख्याएँ ज्ञात कीजिए।
उत्तर : किन्हीं भी दो भिन्न-भिन्न वास्तविक संख्याओं के बीच अनंत संख्या में अपरिमेय संख्याएँ होती हैं (चाहे वे परिमेय हों या अपरिमेय)
1/7 = 0.142857… और 2/7 = 0.285714…
इसलिए, 1/7 और 2/7 के बीच तीन अपरिमेय संख्याएँ 0.150150015000…, 0.20200200020000… और 0.252255222555…
Find three irrational numbers between 1/7 and 2/7.
Answer : There are an infinite number of irrational numbers between any two distinct real numbers (whether they are rational or irrational)
1/7 = 0.142857.… and 2/7 = 0.285714….
Three irrational numbers between 1/7 and 2/7 0.150150015000…, 0.20200200020000… and 0.252255222555…
28. उपयुक्त सर्वसमिका का प्रयोग करके (–2x + 3y + 2z)2 का प्रसार कीजिए।
उत्तर : सर्वसमिका का प्रयोग, (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
यहाँ, a = –2x, b = 3y, c = 2z
(–2x + 3y + 2z)2 = (–2x)2 + (3y)2 + (2z)2 + 2(–2x)(3y) + 2(3y)(2z) + 2(2z)(–2x)
= 4x2 + 9y2 + 4z2 – 12xy + 12yz – 8zx
Expand (–2x + 3y + 2z)2 using suitable identity.
Answer : Using the identity, (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Here, a = –2x, b = 3y, c = 2z
(–2x + 3y + 2z)2 = (–2x)2 + (3y)2 + (2z)2 + 2(–2x)(3y) + 2(3y)(2z) + 2(2z)(–2x)
= 4x2 + 9y2 + 4z2 – 12xy + 12yz – 8zx
29. (x – 2y/3)3 को प्रसारित रूप में लिखिए।
उत्तर : सर्वसमिका का प्रयोग, (a – b)3 = a3 – b3 – 3ab(a – b)
यहाँ, a = x, b = 2y/3
(x – 2y/3)3 = x3 – (2y/3)3 – 3(x)(2y/3)(x – 2y/3)
= x3 – (8/27)y3 – 2xy(x – 2y/3)
= x3 – (8/27)y3 – 2x2y + (4/3)xy2
= x3 – 2x2y + (4/3)xy2 – (8/27)y3
Expand (x – 2y/3)3.
Answer : Using the identity, (a – b)3 = a3 – b3 – 3ab(a – b)
Here, a = x, b = 2y/3
(x – 2y/3)3 = x3 – (2y/3)3 – 3(x)(2y/3)(x – 2y/3)
= x3 – (8/27)y3 – 2xy(x – 2y/3)
= x3 – (8/27)y3 – 2x2y + (4/3)xy2
= x3 – 2x2y + (4/3)xy2 – (8/27)y3
OR
27y3 + 125z3 का गुणनखण्ड ज्ञात कीजिए।
उत्तर : 27y3 + 125z3 = (3y)3 + (5z)3
सर्वसमिका का प्रयोग, (a3 + b3) = (a + b)(a2 – ab + b2)
यहाँ, a = 3y and b = 5z
= (3y + 5z)[(3y)2 – (3y)(5z) + (5z)2]
= (3y + 5z)(9y2 – 15yz + 25z2)
Factorize 27y3 + 125z3.
Answer : 27y3 + 125z3 = (3y)3 + (5z)3
Using the identity, (a3 + b3) = (a + b)(a2 – ab + b2)
Here, a = 3y and b = 5z
= (3y + 5z)[(3y)2 – (3y)(5z) + (5z)2]
= (3y + 5z)(9y2 – 15yz + 25z2)
30. आकृति में, यदि AC = BD है, तो सिद्ध कीजिए कि AB = CD है।

उत्तर : AC = BD…..(i) (दिया गया है)
AC = AB + BC…..(ii) (बिंदु B, A और C के बीच स्थित है)
BD = BC + CD ….. (iii) (बिंदु C, B और D के बीच स्थित है)
समीकरण (ii) और (iii) को (i) में रखने पर,
AB + BC = BC + CD
दोनों पक्षों से उभयनिष्ठ रेखाखंड BC घटाने पर,
AB = CD
अतः सिद्ध हुआ
In fig., if AC = BD, then prove that AB = CD.

Answer : AC = BD …..(i) (Given)
AC = AB + BC …..(ii) (Point B lines between A and C)
BD = BC + CD ….. (iii) (Point C lines between B and D)
Substituting eqn.(ii) and (iii) in (i), we get
AB + BC = BC + CD
Subtract the common segment BC from both sides,
AB = CD
Hence proved
31. एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 cm2 है और इसकी तिर्यक ऊँचाई 14 cm है। ज्ञात कीजिए (i) आधार की त्रिज्या (ii) शंकु का कुल पृष्ठीय क्षेत्रफल।
उत्तर : (i) तिर्यक ऊँचाई, l = 14 cm
वक्र पृष्ठीय क्षेत्रफल = 308 cm2
πrl = 308
22/7 × r × 14 = 308
44 × r = 308
r = 308/44 = 7 cm
आधार की त्रिज्या 7 cm है।
(ii) कुल पृष्ठीय क्षेत्रफल = πr(r + l)
= 22/7 × 7 × (7 + 14)
= 22 × 21
= 462 cm2
शंकु का कुल पृष्ठीय क्षेत्रफल 462 cm2 है।
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find (i) radius of the base and (ii) total surface area of the cone.
Answer : (i) Slant height, l = 14 cm
Curved surface area = 308 cm2
πrl = 308
22/7 × r × 14 = 308
44 × r = 308
r = 308/44 = 7 cm
The radius of the base is 7 cm.
(ii) Total surface area = πr(r + l)
= 22/7 × 7 × (7 + 14)
= 22 × 21
= 462 cm2
The total surface area of cone is 462 cm2.
OR
उस गोले का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm2 है।
उत्तर : गोले का पृष्ठीय क्षेत्रफल = 4πr2
4πr2 = 154
r2 = 154 × 1/4 × 7/22
r2 = 49/4
r = √49/4
r = 7/2 cm
गोले का आयतन = 4/3πr3
= 4/3 × 22/7 × 7/2 × 7/2 × 7/2
= 539/3 cm3
गोले का आयतन 539/3 cm3 है।
Find the volume of a sphere whose surface area is 154 cm2.
Answer : Surface area of the sphere = 4πr2
4πr2 = 154
r2 = 154 × 1/4 × 7/22
r2 = 49/4
r = √49/4
r = 7/2 cm
Volume of the sphere = 4/3πr3
= 4/3 × 22/7 × 7/2 × 7/2 × 7/2
= 539/3 cm3
The volume of the sphere is 539/3 cm3.
SECTION – D (5 Marks)
32. 8x3 + y3 + 27z3 – 18xyz का गुणनखण्ड कीजिए।
उत्तर : 8x3 + y3 + 27z3 – 18xyz = (2x)3 + y3 + (3z)3 – 3(2x)(y)(3z)
सर्वसमिका का प्रयोग, a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
यहाँ, a = 2x, b = y, c = 3z
= (2x + y + 3z)[(2x)2 + y2 + (3z)2 – (2x)(y) – (y)(3z) – (2x)(3z)]
= (2x + y + 3z)(4x2 + y2 + 9z2 – 2xy – 3yz – 6xz)
Factorize 8x3 + y3 + 27z3 – 18xyz.
Answer : 8x3 + y3 + 27z3 – 18xyz = (2x)3 + y3 + (3z)3 – 3(2x)(y)(3z)
Using the identity, a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
Here, a = 2x, b = y, c = 3z
= (2x + y + 3z)[(2x)2 + y2 + (3z)2 – (2x)(y) – (y)(3z) – (2x)(3z)]
= (2x + y + 3z)(4x2 + y2 + 9z2 – 2xy – 3yz – 6xz)
OR
8x3 + 27y3 + 36x2y + 54xy2 का गुणनखण्ड कीजिए।
उत्तर : 8x3 + 27y3 + 36x2y + 54xy2 = (2x)3 + (3y)3 + 36x2y + 54xy2
= (2x)3 + (3y)3 + 18xy(2x + 3y)
= (2x)3 + (3y)3 + 3(2x)(3y)(2x + 3y)
सर्वसमिका का प्रयोग, (a + b)3 = a3 + b3 + 3ab(a + b)
Here, a = 2x, b = 3y
= (2x + 3y)3
= (2x + 3y)(2x + 3y)(2x + 3y)
Factorize 8x3 + 27y3 + 36x2y + 54xy2.
Answer : 8x3 + 27y3 + 36x2y + 54xy2 = (2x)3 + (3y)3 + 36x2y + 54xy2
= (2x)3 + (3y)3 + 18xy(2x + 3y)
= (2x)3 + (3y)3 + 3(2x)(3y)(2x + 3y)
Using the identity, (a + b)3 = a3 + b3 + 3ab(a + b)
Here, a = 2x, b = 3y
= (2x + 3y)3
= (2x + 3y)(2x + 3y)(2x + 3y)
33. आकृति में, यदि AB || CD, ∠APQ = 50° और ∠PRD = 127° है, तो x और y ज्ञात कीजिए।
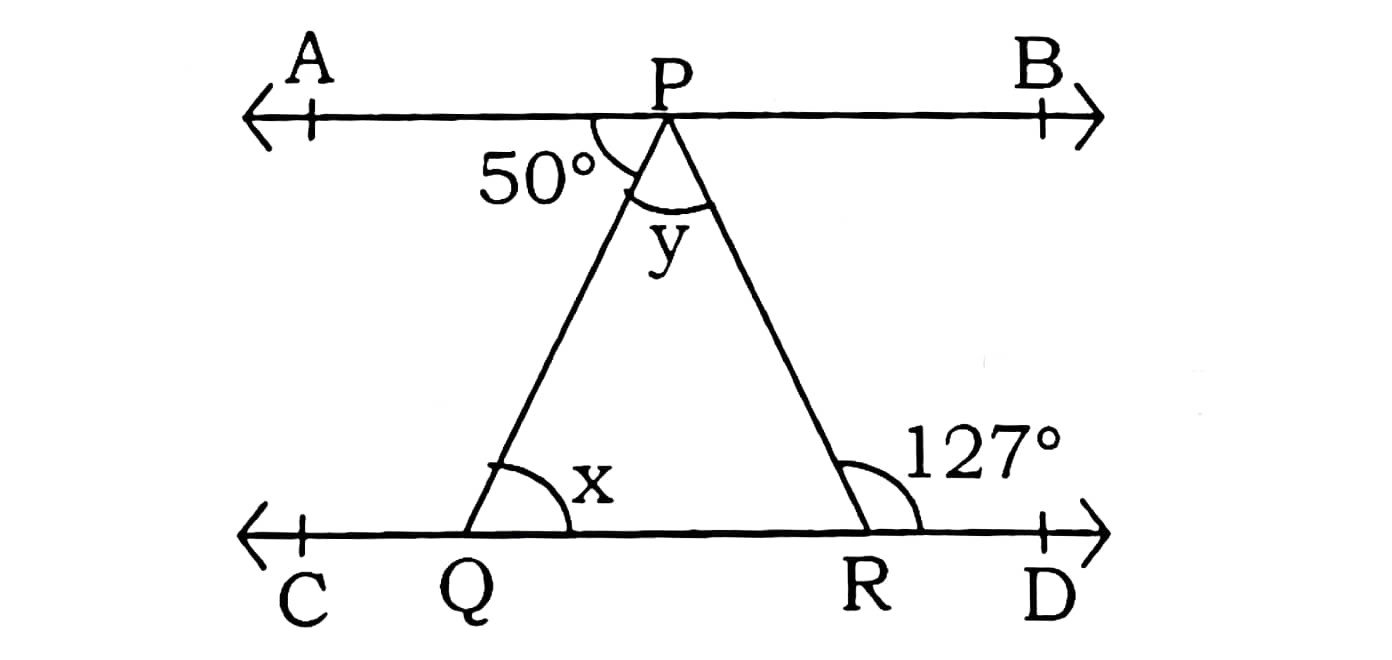
उत्तर : दिया गया है, ∠APQ = 50°, ∠PRD = 127°
∠APQ = ∠PQR (एकांतर अंतः कोण)
अतः, x = 50°
∠APR = ∠PRD = 127° (एकांतर अंतः कोण)
अतः, ∠APQ + ∠QPR = ∠PRD
50° + y = 127°
y = 127° – 50°
y = 77°
इसलिए x = 50° और y = 77° मान हैं।
In fig., if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.

Answer : Given, ∠APQ = 50°, ∠PRD = 127°
∠APQ = ∠PQR (alternate interior angles)
so, x = 50°
∠APR = ∠PRD = 127°(alternate interior angles)
so, ∠APQ + ∠QPR = ∠PRD
50° + y = 127°
y = 127° – 50°
y = 77°
The values for x = 50° and y = 77°.
34. ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं (देखिए आकृति)। दर्शाइए कि ∠ABD = ∠ACD है।

उत्तर : दिया गया है: ABC और DBC समद्विबाहु त्रिभुज हैं।
सिद्ध करना है: ∠ABD = ∠ACD
∆ABC में,
∠ABC = ∠ACB ….(i) (क्योंकि AB = AC)
∆DBC में,
∠DBC = ∠DCB ….(ii) (क्योंकि DB = DC)
इसलिए (i) और (ii) को जोड़ने पर,
∠ABC + ∠DBC = ∠ACB + ∠DCB
अतः, ∠ABD = ∠ACD
ABC and DBC are two isosceles triangles on the same base BC (see in fig). Show that ∠ABD = ∠ACD.

Answer :
Given: ABC and DBC are isosceles triangles
To Prove: ∠ABD = ∠ACD
In ∆ABC,
∠ABC = ∠ACB ….(i) (because AB = AC)
In ∆DBC,
∠DBC = ∠DCB ….(ii) (because DB = DC)
Adding (i) and (ii), we get
∠ABC + ∠DBC = ∠ACB + ∠DCB
Hence, ∠ABD = ∠ACD
35. एक त्रिभुजाकार भूखंड (Plot) की भुजाओं का अनुपात 3 : 5 : 7 है और उसका परिमाप 300 m है। इस भूखंड का क्षेत्रफल ज्ञात कीजिए।
उत्तर : मान लीजिए, a = 3x, b = 5x, c = 7x
परिधि (P) = a + b + c
3x + 5x + 7x = 300
15x = 300
x = 300/15 = 20
a = 3x = 3 × 20 = 60 m
b = 5x = 5 × 20 = 100 m
c = 7x = 7 × 20 = 140 m
अर्ध-परिधि (s) = 300/2 = 150 m
हीरोन के सूत्र का प्रयोग करते हुए,
त्रिभुज का क्षेत्रफल = √s(s–a)(s–b)(s–c)
A = √150(150–60)(150–100)(150–140)
= √150(90)(50)(10)
= 1500√3 m2
The sides of a triangular plot are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find its area.
Answer : Let, a = 3x, b = 5x, c = 7x
Perimeter (P) = a + b + c
3x + 5x + 7x = 300
15x = 300
x = 300/15 = 20
a = 3x = 3 × 20 = 60 m
b = 5x = 5 × 20 = 100 m
c = 7x = 7 × 20 = 140 m
Semi Perimeter (s) = 300/2 = 150 m
Using Heron’s Formula,
Area of triangle = √s(s–a)(s–b)(s–c)
A = √150(150–60)(150–100)(150–140)
= √150(90)(50)(10)
= 1500√3 m2
OR
एक लंब वृत्तीय शंकु का आयतन 9856 cm3 है। यदि इसके आधार का व्यास 28 cm है, तो ज्ञात कीजिए :
(i) शंकु की ऊँचाई
उत्तर : व्यास = 28 cm
त्रिज्या (r) = व्यास/2 = 28/2 = 14 cm
शंकु का आयतन = 9856 cm3
1/3πr2h = 9856
1/3 × 22/7 × 14 × 14 × h = 9856
h = 9856 × 3 × 7/22 × 1/14 × 1/14
h = 48 cm
(ii) शंकु की तिर्यक ऊँचाई
उत्तर : तिर्यक ऊँचाई, l = √r2+h2
l = √(14)2+(48)2 = √196+2304 = √2500
l = 50 cm
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल
उत्तर : वक्र पृष्ठीय क्षेत्रफल क्षेत्रफल, CSA = πrl
= 22/7 × 14 × 50
= 2200 cm2
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm. Find :
(i) Height of the cone
Answer : Diameter = 28 cm
Radius (r) = Diameter/2 = 28/2 = 14 cm
Volume of the cone = 9856 cm3
1/3πr2h = 9856
1/3 × 22/7 × 14 × 14 × h = 9856
h = 9856 × 3 × 7/22 × 1/14 × 1/14
h = 48 cm
(ii) Slant Height of the cone
Answer : Slant height, l = √r2+h2
l = √(14)2+(48)2 = √196+2304 = √2500
l = 50 cm
(iii) Curved surface area of cone
Answer : Curved surface area, CSA = πrl
= 22/7 × 14 × 50
= 2200 cm2
SECTION – E (4 Marks : CASE STUDY)
36. पाँच दोस्त अलग-अलग बिंदुओं P, Q, R, S और T पर खड़े होकर एक खेल, खेल रहे हैं। रोहन उन्हें खेलता हुआ देख रहा है। रोहन के दिमाग में उन्हें खेलते हुए देखकर कुछ प्रश्न आ रहे हैं।
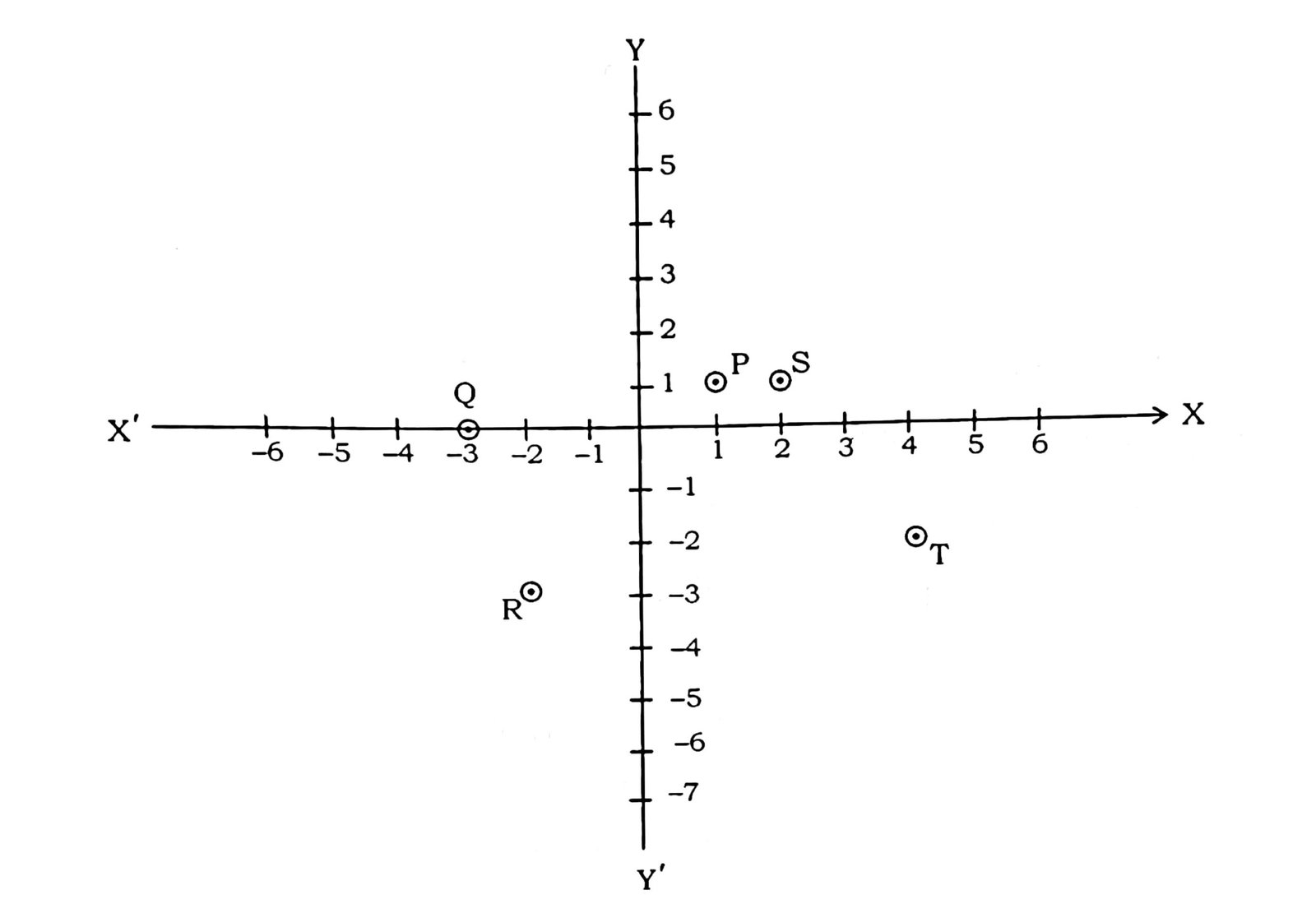
आकृति को देखकर प्रश्नों के उत्तर दीजिए :
(i) उस बिंदु का नाम बताइए, जिसका Y-निर्देशांक शून्य है।
उत्तर : Q
(ii) तृतीय चतुर्थांश में कौन-सा बिंदु है?
उत्तर : R
(iii) बिन्दु P के निर्देशांक क्या हैं?
उत्तर : (1, 1)
(iv) बिन्दु T के निर्देशांक क्या हैं?
उत्तर : (4, –2)
Five friends are playing a game in which they are standing at different position P, Q, R, S and T. Rohan is watching them playing. Few questions came to Rohan’s mind while watching the game.

Give answer to the questions by looking at the figure :
(i) Name the point whose Y-coordinate is zero.
Answer : Q
(ii) Name the point lying in the third quadrant.
Answer : R
(iii) What are the coordinates of P?
Answer : (1, 1)
(iv) What are the coordinates of T?
Answer : (4, –2)
37. कोविड-19 महामारी, जिसे कोरोना वायरस महामारी के रूप में भी जाना जाता है, गंभीर तीव्र श्वसन सिंड्रोम कोरोना वायरस 2 (SARS-COV-2) के कारण होने वाली कोरोना वायरस बीमारी 2019 की एक चल रही महामारी थी। इसकी पहचान पहली बार दिसम्बर, 2019 में चीन के वुहान में हुई थी। सर्वेक्षण के दौरान शहर के एक अस्पताल में भर्ती कोविड से संक्रमित 80 रोगियों की आयु दर्ज की गई और एकत्र किए गए डेटा को संचयी वितरण तालिका में दर्शाया गया है :
| आयु (वर्षों में) | मरीजों की संख्या |
| 5-15 | 6 |
| 15-25 | 11 |
| 25-35 | 21 |
| 35-45 | 23 |
| 45-55 | 14 |
| 55-65 | 5 |
उपरोक्त जानकारी के अनुसार निम्न प्रश्नों के उत्तर दीजिए :
(i) उच्चतम आवृत्ति वाला वर्ग अंतराल बताइए।
उत्तर : 35-45
(ii) कौन-सा आयु वर्ग सबसे कम प्रभावित हुआ?
उत्तर : 55-65
(iii) कौन-सा आयु वर्ग सबसे अधिक प्रभावित हुआ?
उत्तर : 35-45
(iv) 45 वर्ष और उससे अधिक आयु के कितने मरीज भर्ती किए गए?
उत्तर : 14 + 5 = 19
The Covid-19 pandemic also known as the Corona virus pandemic. It is an ongoing pandemic of Corona virus disease 2019 caused by Severe Acute Respiratory Syndrome Corona Virus-2 (SARS-COV-2). It was first identified in December, 2019 in Wuhan, China. A data was collected of 80 patients admitted in a hospital who were infected with COVID is shown in the cumulative frequency distribution table :
| Age (In Years) | No. of Patients |
| 5-15 | 6 |
| 15-25 | 11 |
| 25-35 | 21 |
| 35-45 | 23 |
| 45-55 | 14 |
| 55-65 | 5 |
Based on the above information, answer the following questions :
(i) State the class interval with the highest frequency.
Answer : 35-45
(ii) Which age group was least affected?
Answer : 55-65
(iii) Which age group was most affected?
Answer : 35-45
(iv) How many patients aged 45 years and above were admitted?
Answer : 14 + 5 = 19
38. राम सरन एक किसान है। उसके पास एक त्रिभुजाकार खेत जिसकी भुजाएँ 240 m, 200 m और 360 m हैं। इसमें वह गेहूँ उगाना चाहता है। इसी खेत के संलग्न 240 m, 320 m और 400 m भुजाओं वाला एक अन्य खेत है, जहाँ वह आलू व प्याज उगाना चाहता है (आकृति में)। उसने खेत की सबसे लम्बी भुजा के मध्य बिंदु को सम्मुख शीर्ष से जोड़कर उसे दो भागों में विभाजित कर दिया। इनमें से एक भाग में उसने आलू उगाए और दूसरे भाग में प्याज उगाए।
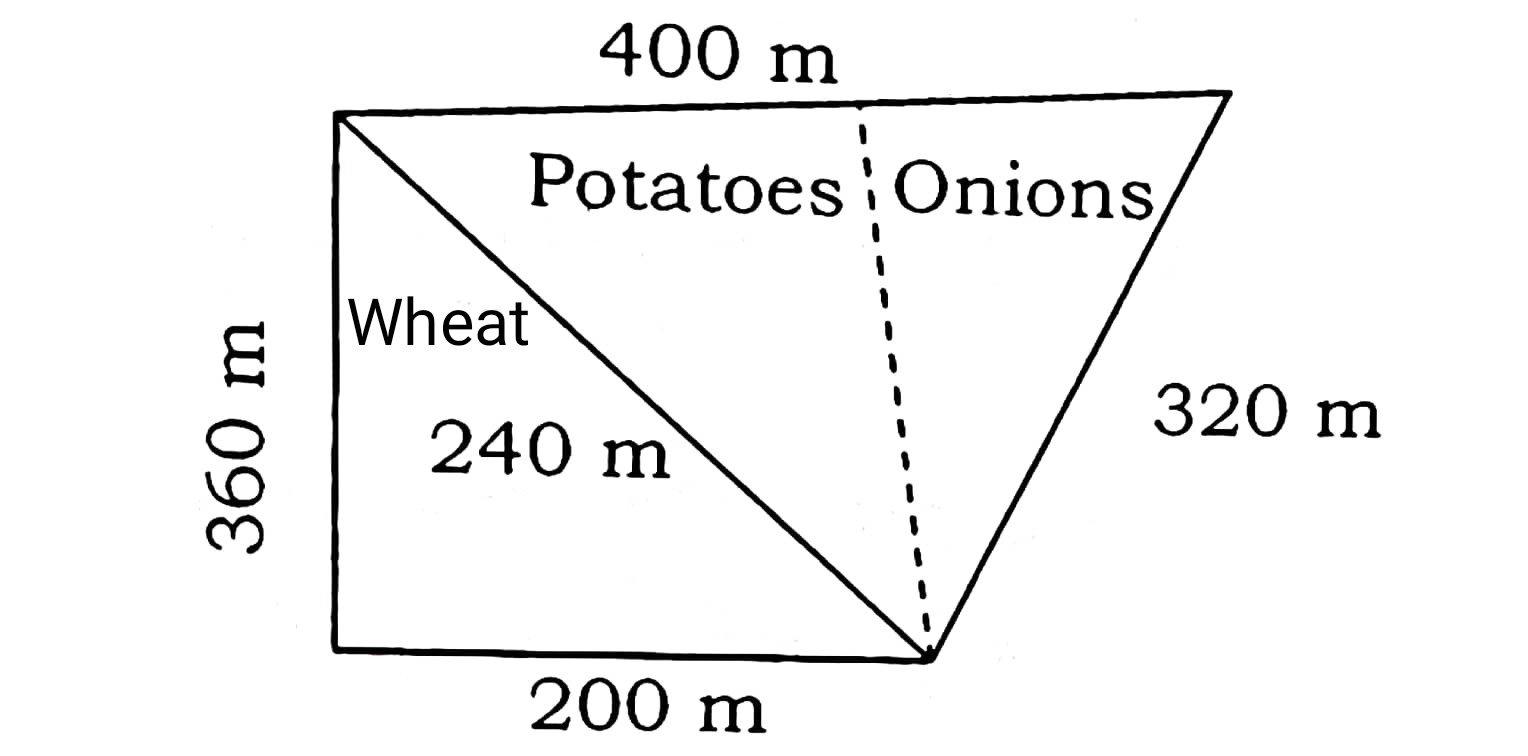
उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) गेहूँ के खेत का अर्द्ध-परिमाप क्या होगा?
उत्तर : s = (a+b+c)/2 = (360+200+240)/2 = 800/2 = 400 m
(ii) उस खेत का अर्द्ध-परिमाप ज्ञात कीजिए, जिसमें वह आलू व प्याज उगाना चाहता है?
उत्तर : s = (a+b+c)/2 = (400+320+240)/2 = 960/2 = 480 m
(iii) पूरे खेत का परिमाप ज्ञात कीजिए।
उत्तर : 360 + 200 + 320 + 400 = 1280 m
Ram Saran is a farmer. He has a triangular shaped field with sides 240 m, 200 m and 360 m, where he wants to grow wheat. Adjoining this field he has another field with sides 240 m, 320 m and 400 m, where he wants to grow potatoes and onions (see in fig.). He divided equally this field into two parts by joining the mid point of longest side with opposite vertices. In one of the field he wants to grow potatoes and in other onions.

Based on the above information answer the following questions :
(i) Find the semi-perimeter of wheat’s field.
Answer : s = (a+b+c)/2 = (360+200+240)/2 = 800/2 = 400 m
(ii) Find the semi-perimeter of field where he wants to grow potatoes and onions.
Answer : s = (a+b+c)/2 = (400+320+240)/2 = 960/2 = 480 m
(iii) Find the perimeter of whole field.
Answer : 360 + 200 + 320 + 400 = 1280 m
