Haryana Board (HBSE) Class 12 Physics Question Paper 2024 with a fully solved answer key. Students can use this HBSE Class 12 Physics Solved Paper to match their responses and understand the question pattern. This BSEH Physics Answer Key 2024 is based on the latest syllabus and exam format to support accurate preparation and revision for the board exams.
HBSE Class 12 Physics Question Paper 2024 Answer Key
SECTION – A (1 Mark)
1. Two point charges +1 µC and –4 µC are situated at some distance in air. The ratio of forces acting on them is :
(A) 1 : 4
(B) 4 : 1
(C) 1 : 16
(D) 1 : 1
Answer – (D) 1 : 1
Forces between two point charges are equal in magnitude and opposite in direction according to Newton’s third law (and Coulomb’s law), so the ratio of forces is 1 : 1 regardless of the magnitude of charges.
2. 1 mA current is flowing through a conductor of 2 kΩ resistance. How much power is lost in it?
(A) 0.2 W
(B) 2 mW
(C) 2 W
(D) 2 kW
Answer – (B) 2 mW
I = 1 mA = 1 × 10–3 A
R = 2 kΩ = 2 × 103 Ω
P = I2R = (1 × 10–3 A)2 × (2 × 103 Ω)
= (1 × 10–6 A2) × (2 × 103 Ω)
= 2 × 10–3 W
= 2 mW
3. A potential difference of 12 V is applied across the ends of a 4 kΩ resistor. How much current is flowing through it?
(A) 3 mA
(B) 3 A
(C) 4 A
(D) 48 mA
Answer – (A) 3 mA
V = 12 V
R = 4 kΩ = 4 × 103 Ω = 4000 Ω
Ohm’s law, I = V/R = 12/4000 = 0.003 A = 3 × 10–3 A = 3 mA
4. The current-voltage (I-V) graphs for a given metallic wire at two temperatures T1 and T2 are shown in Fig. (Q. No. 4). Then :
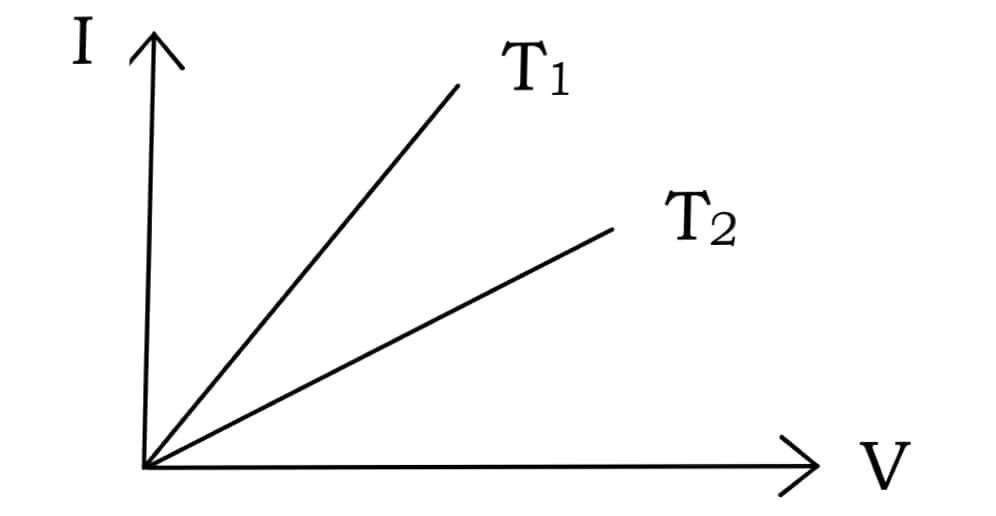
(A) T1 = T2
(B) T1 > T2
(C) T2 > T1
(D) None of the above
Answer – (C) T2 > T1
5. The SI unit of magnetic dipole moment of a bar magnet is :
(A) Am–2
(B) Am–1
(C) Am
(D) Am2
Answer – (D) Am2
6. The relation between magnetic susceptibility χ and relative permeability µr of a magnetic material is :
(Α) µr = 1 + χ
(Β) µr = 1 + χ2
(C) µr = 1/χ
(D) µr = 1 – χ2
Answer – (Α) µr = 1 + χ
7. For an alternating current i = Iosinωt passing through a resistor R, how much is the average power loss due to Joule heating?
(A) Io2R
(B) ½ Io2R
(C) 4 Io2R
(D) 2 Io2R
Answer – (B) ½ Io2R
Average power (Pavg) = I2rmsR
Irms = Io/√2
P = I2R = (Io/√2)2R = ½ Io2R
8. What is the value of resonant frequency ωo of a series LCR circuit?
(A) LC
(B) 1/(LC)
(C) √(LC)
(D) 1/√(LC)
Answer – (D) 1/√(LC)
9. Which of the following have lowest wavelength in vacuum?
(A) Infrared waves
(B) X-rays
(C) Visible light waves
(D) Radio waves
Answer – (B) X-rays
10. The refractive index of a medium having critical angle of 60° is :
(A) √3/2
(B) 2/√3
(C) 1/3
(D) 1/√2
Answer – (B) 2/√3
Refractive index (n) = 1/sinC = 1/sin60° = 1/(√3/2) = 2/√3
11. K is the kinetic energy of a moving particle of mass m. The de-Broglie wavelength λ associated with this particle is :
(A) h/K
(B) h/(2K)
(C) 2h/√(2mK)
(D) h/√(2mK)
Answer – (D) h/√(2mK)
12. Which spectral series of hydrogen atom lies in the visible region?
(A) Balmer series
(B) Lyman series
(C) Paschen series
(D) Bracket series
Answer – (A) Balmer series
13. The net charge on an atom of atomic number Z as a whole is :
(A) +Ze
(B) –Ze
(C) Zero
(D) +(Z–1)e
Answer – (C) Zero
14. One atomic mass unit (1u) equals :
(A) 1.660539 × 10–27 kg
(B) 1.660539 × 10–23 kg
(C) 1.660539 × 10–17 kg
(D) 1.660539 × 10–13 kg
Answer – (A) 1.660539 × 10–27 kg
15. Assertion (A) : When a narrow beam of white light passes through a glass prism, it undergoes dispersion.
Reason (R) : The refractive index of medium for different wavelengths (colours) is different.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true, but Reason (R) is false.
(D) Both Assertion (A) and Reason (R) are false.
Answer – (A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
16. Assertion (A) : The photoelectrons produced by a monochromatic light beam incident on a metal surface have a spread in their kinetic energies.
Reason (R) : Work function is the least energy required by an electron to come out of the metal.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true, but Reason (R) is false.
(D) Both Assertion (A) and Reason (R) are false.
Answer – (B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
17. Assertion (A) : The resistivity of a n-type semiconductor decreases with an increase in temperature.
Reason (R) : The rate of collision between free electrons and the ions increase with an increase in temperature.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true, but Reason (R) is false.
(D) Both Assertion (A) and Reason (R) are false.
Answer – (B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
18. Assertion (A) : The electrical conductivity of an intrinsic semiconductor increases on doping.
Reason (R) : Doping always increases the number of free electrons in a pure semiconductor.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true, but Reason (R) is false.
(D) Both Assertion (A) and Reason (R) are false.
Answer – (C) Assertion (A) is true, but Reason (R) is false.
SECTION – B (2 Marks)
19. Define relaxation time of free electrons in a metal. Write the relation between drift velocity of free electrons and their relaxation time.
Answer – Relaxation time is the average time for which an electron continues to move freely between two consecutive collisions with the fixed ions or atoms in the metal lattice. The drift velocity (vd) of free electrons is related to the relaxation time (τ) by the relation:
vd = – eEτ/m
where e is the charge of an electron, E is the applied electric field, and m is the mass of an electron.
20. State Ampere’s circuital law and explain it briefly using a diagram.
Answer – Ampere’s circuital law states that the line integral of the magnetic field (B) around any closed loop is equal to the permeability of free space (μo) multiplied by the total current (Iencl) enclosed by that loop.
Mathematically, ∮B.dl = μoI
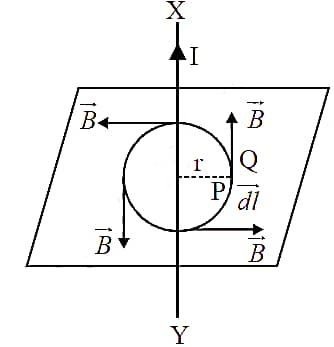
OR
State Biot-Savart’s law using a diagram.
Answer – Biot-Savart’s law states that the magnetic field (dB) produced at a point by a current carrying conductor is directly proportional to the current (I) flowing through the conductor, the length of the small current element (dl), and sinθ, where θ is the angle between the current element and the line joining it to the observation point. It is inversely proportional to the square of the distance between the conductor and that point.
Mathematically, dB = μo/4π × Idlsinθ/r2
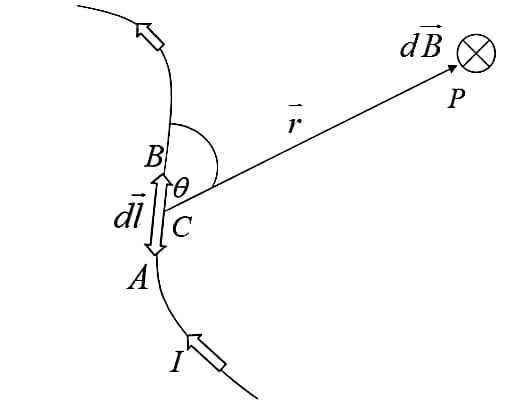
21. A 30 µF capacitor is connected to a 220 V, 50 Hz source. Find the capacitive reactance and the rms value of the current in the circuit.
Answer – Given, f = 50 Hz, V = 220 V, C = 30 µF = 30 × 10–6 F
Capacitive reactance (XC) = 1/2πfC
XC = 1/(2×3.14×50×30×10–6) = 106.1 Ω
RMS Current (Irms) = Vrms/XC
Irms = 220/106.1 = 2.07 A
The capacitive reactance is approximately 106.1 Ω and the rms value of the current in the circuit is approximately 2.07 A.
OR
A power transmission line feeds input power at 2200 V to a step down transformer with its primary windings having 4000 turns. What should be the number of turns in the secondary in order to get output power at 220 V ?
Answer – Given, Vp = 2200 V, Vs = 220 V, Np = 4000 turns
The relationship for an ideal transformer is given by the turns ratio formula:
Vp/Vs = Ns/Np
Now calculate secondary turns:
Ns = Np × Vs/Vp = 4000 × 220/2200 = 400 turns
22. What are electromagnetic waves? What is their nature?
Answer – Electromagnetic (EM) waves are waves of oscillating electric and magnetic fields that propagate through space, transferring energy. Their nature is that they are transverse waves, meaning the electric and magnetic fields oscillate perpendicular to each other and to the direction the wave is traveling. These waves can travel through a vacuum at the speed of light and do not require a material medium to move.
23. A convex lens of refractive index 1.5 has a focal length of 15 cm in air. What will be its focal length when it is immersed in a liquid of refractive index 4/3?
Answer – Given, fair = 15 cm, nlens = 1.5
The lensmaker’s equation in air (refractive index nair = 1) is given by:
1/fair = (nlens/nair – 1)(1/R1 – 1/R2)
1/15 = (1.5/1 – 1)C
Lens constant (C) = 2/15 cm–1
When immersed in the liquid with refractive index nliquid = 4/3, the new relative refractive index n’ is:
n’ = nlens/nliquid = 1.5 / (4/3) = 9/8
The lensmaker’s equation in liquid is:
1/fliquid = (n’ – 1)C = (9/8 – 1) × 2/15 = 1/8 × 2/15 = 1/60
fliquid = 60 cm
24. Explain total internal reflection by a ray diagram.
Answer – Total internal reflection occurs when a light ray travels from a denser medium to a rarer medium and the angle of incidence becomes greater than the critical angle (ic). Under this condition, the light ray does not refract into the second medium but is completely reflected back into the denser medium.
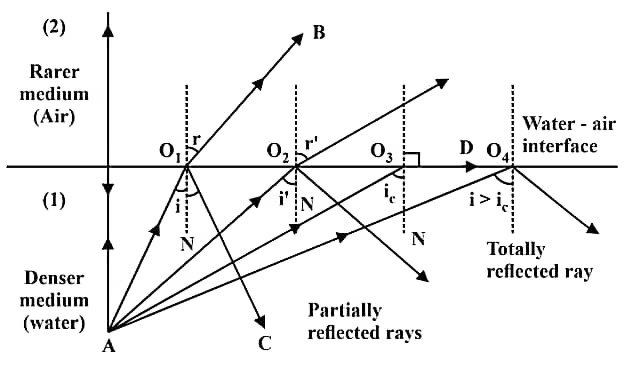
25. The total energy of the electron in the nth orbit of hydrogen atom is En = – 13.6/n2 eV. Calculate its kinetic and potential energies in this orbit.
Answer – Kinetic energy is always positive and equal to the magnitude of total energy:
Κ.Ε. = – En
Κ.Ε. = –(–13.6/n2) eV = 13.6/n2 eV
Potential energy is always negative and is twice the total energy:
P.E. = 2En
P.E. = 2(–13.6/n2) = – 27.2/n2 eV
SECTION – C (3 Marks)
26. State the Gauss’s law of electrostatics. Using it prove that electric field inside a uniformly charged thin spherical shell is zero.
Answer – Gauss’s law states that the total electric flux through any closed surface is equal to the net charge enclosed by that surface divided by the permittivity of free space (∈o) .
Mathematically, ∮E.dA = Q/∈o
Here, ∮E.dA = E × 4πr2
Since this Gaussian surface lies entirely inside the charged shell, it encloses no charge (Qencl = 0)
E × 4πr2 = Q/∈o = 0/∈o = 0
E = 0
Hence, the electric field inside a uniformly charged thin spherical shell is zero.
OR
(a) Define electrostatic potential at a point in an electric field.
Answer – Electrostatic potential at a point in an electric field is defined as the amount of work done in bringing a unit positive charge from infinity to that point, without any acceleration. Its SI unit is volt (V).
(b) A 600 µF capacitor is charged by a 10 V battery. How much electrostatic energy is stored in the capacitor?
Answer – The given values for the capacitor and battery are:
Capacitance (C) = 600 µF = 6 × 10–4 F
Voltage (V) = 10V
Electrostatic energy (U) = ½ CV2
U = ½ (6 × 10–4)(10)2 = 0.03 J
The electrostatic energy stored in the capacitor is 0.03 J.
27. Write the principle of meter bridge. Draw its circuit diagram to determine the value of an unknown resistance.
Answer – The principle of a meter bridge is based on the balanced condition of a Wheatstone bridge. At balance, no current flows through the galvanometer, and the ratio of the resistances in the two arms equals the ratio of the lengths of the wire on the meter bridge. Thus, an unknown resistance can be determined by comparing it with a known resistance.

Arrange the circuit as shown in figure,
Close the key K and take out suitable resistance R from resistance box. Slide the jockey to find balancing length.
Let AB = l = balancing length
BC = (100 – l)
According to Wheat stone bridge principle
P/Q = R/S
If r is resistance per unit length of wire
when (lr)/(100–l) = R/S
S = (100–l)/l × R
OR
Write Kirchoff’s Law of Electrical Circuit.
Answer – Kirchhoff’s Laws of Electrical Circuits :
(i) Kirchhoff’s Current Law (KCL) – It states that the total current entering a junction is equal to the total current leaving it. This law is based on the conservation of charge and implies that no charge accumulates at a node.
(ii) Kirchhoff’s Voltage Law (KVL) – It states that the algebraic sum of all voltage drops and emfs in any closed loop of a circuit is zero. This law follows from the conservation of energy, meaning the total potential rise equals the total potential drop in a loop.
28. In Young’s double slit experiment, the ratio of width of two slits is 4 : 1. Find the ratio of maximum and minimum intensities in the interference pattern.
Answer – As, Intensity ∝ width of slit (w)
Also, Intensity ∝ square of amplitude (A2)
I1/I2 = w1/w2 = A12/A22 = 4/1
A1/A2 = √4/√1 = 2/1
so, amplitude ratio = A1 : A2 = 2 : 1
Imax = (A1 + A2)2 = (2 + 1)2 = 32 = 9
Imin = (A1 – A2)2 = (2 – 1)2 = 12 = 1
Imax : Imin = 9 : 1
Ratio of maximum to minimum intensities = 9 : 1
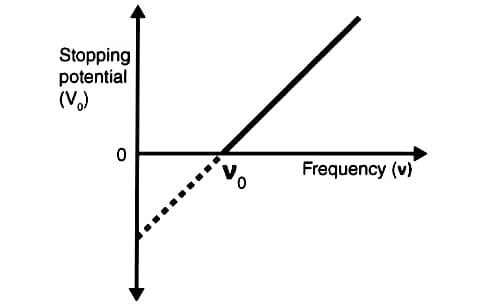
29. Draw a graph showing effect of frequency of incident radiation on stopping potential. Explain it by using Einstein’s photoelectric equation.
Answer – Einstein’s photoelectric equation explains how the stopping potential depends on the frequency of incident radiation. The equation is: [E = hf – ɸ], where (E) is the kinetic energy of emitted electrons, (h) is Planck’s constant, (f) is the frequency of the incident radiation, and (ɸ) is the work function of the material.
The stopping potential (Vo) relates to the maximum kinetic energy of emitted electrons as: [eVo = hf – ɸ].
30. State Bohr Postulates of Hydrogen atom.
Answer – Bohr’s Postulates of the Hydrogen Atom are :
• Postulate 1 : Stationary Orbits
An electron in a hydrogen atom revolves around the nucleus only in certain fixed circular paths called stationary orbits. Each of these orbits has a definite energy, and the electron does not radiate energy while moving in them. The necessary centripetal force for the circular motion is provided by the electrostatic attraction between the positively charged nucleus and the negatively charged electron.
• Postulate 2 : Quantisation of Angular Momentum
Only those orbits are allowed in which the angular momentum of the electron is quantised. This means the angular momentum can have only specific discrete values, given by:
mvr = nh/2π
• Postulate 3 : Energy Transitions and Photons
An electron can move from one stationary orbit to another only by absorbing or emitting a photon whose energy equals the difference between the two orbits. When it jumps to a higher orbit, it absorbs energy; when it falls to a lower orbit, it emits energy.
Energy of the photon, ∆E = E2 – E1 = hf
SECTION – D (5 Marks)
31. Write the principle of a moving coil galvanometer. How is it converted into an ammeter? Write the expression for its current sensitivity.
Answer – The principle of a moving-coil galvanometer is based on the fact that when a current-carrying coil is placed in a magnetic field, it experiences a torque. This torque is proportional to the current flowing through the coil. As the coil turns, a restoring torque is provided by the suspension or spring. At equilibrium, the deflection of the coil becomes proportional to the current, so the galvanometer can measure small currents accurately.
A galvanometer is converted into an ammeter by connecting a low-resistance shunt in parallel with it. Since an ammeter is used to measure large currents, the shunt provides an alternate path, allowing most of the current to bypass the galvanometer. This prevents damage to the coil and enables the device to measure higher currents while keeping the galvanometer’s deflection within safe limits.
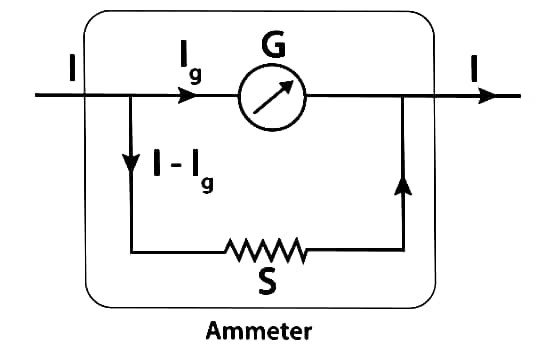
Current sensitivity (SI) = θ/I = nAB/k
OR
Write the principle of a moving coil galvanometer. How is it converted into a voltmeter? Write the expression for its voltage sensitivity.
Answer – The principle of a moving-coil galvanometer is based on the fact that when a current-carrying coil is placed in a uniform magnetic field, it experiences a magnetic torque. This torque is directly proportional to the current flowing through the coil. A restoring torque provided by the suspension or spring balances it, and at equilibrium, the angular deflection of the coil becomes proportional to the current, allowing the galvanometer to detect very small currents with high sensitivity.
A galvanometer is converted into a voltmeter by connecting a high resistance (R) in series with its coil. Since a voltmeter is used to measure potential difference across a circuit, only a small current should pass through it. The added high resistance reduces the current through the galvanometer, enabling it to measure larger potential differences safely while ensuring that the voltmeter draws negligible current from the circuit.
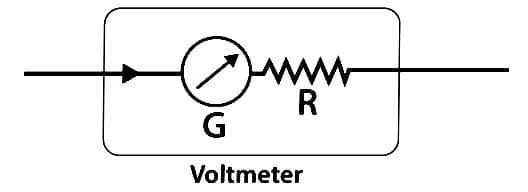
Voltage sensitivity (SV) = θ/I = nAB/k(R+G)
32. Draw a labelled ray diagram showing the image formation in a refracting astronomical telescope and explain it. Define its magnifying power and write expression for it.
Answer – An astronomical telescope consists of a convex objective lens of large focal length and a convex eyepiece of short focal length.
In normal adjustment, the final image is formed at infinity.
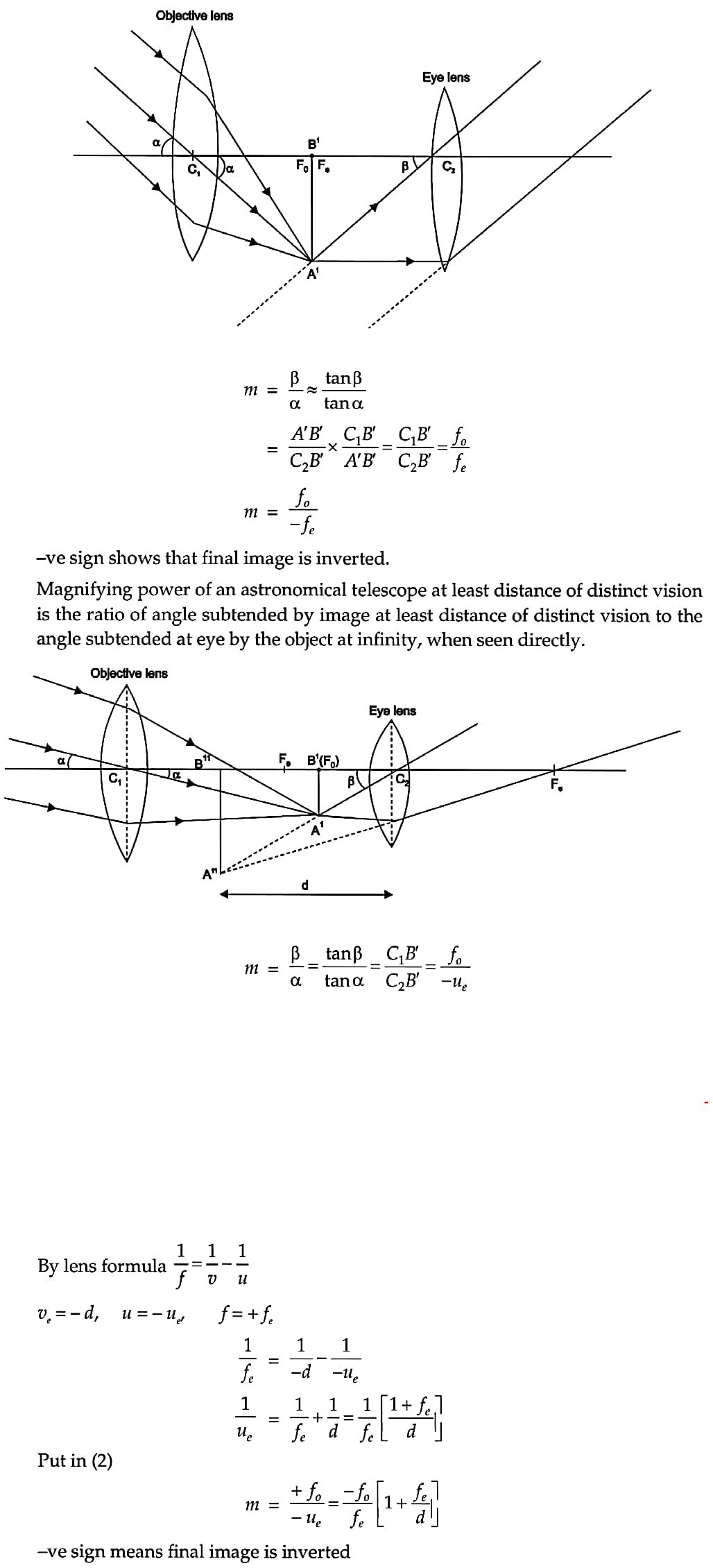
OR
Draw a labelled ray diagram showing the image formation in a compound microscope and explain it. Define its magnifying power and write expression for it.
Answer –

33. What is a rectifier? Draw the circuit diagram of a full-wave rectifier. Explain its input and output voltage waveforms.
Answer – A rectifier is an electronic device that converts alternating current (AC) into direct current (DC) by allowing current to flow in only one direction.
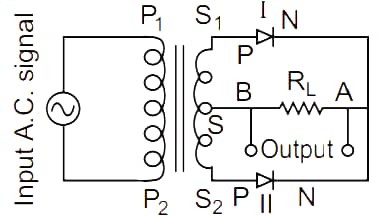
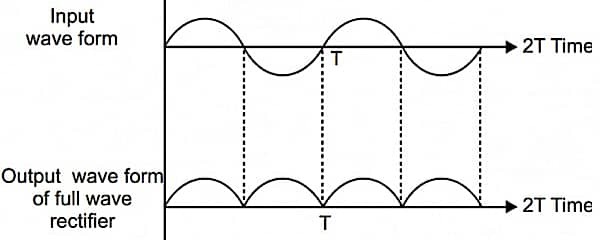
In a full-wave rectifier, the AC input voltage is sinusoidal. During the positive half-cycle, one diode conducts while the other remains reverse-biased. The conducting diode allows current through the load resistor, producing a positive output.
During the negative half-cycle, the second diode becomes forward-biased, and the first diode is reverse-biased. This diode again drives current through the load in the same direction as before.
Thus, although the input AC has both positive and negative half-cycles, the output contains only positive pulsations for both halves, giving a smooth sequence of pulses known as pulsating DC.
OR
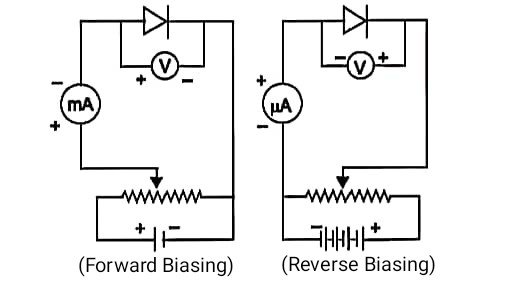
Draw the I-V characteristics of a p-n junction diode in forward and reverse bias. Explain them using appropriate circuit diagrams.
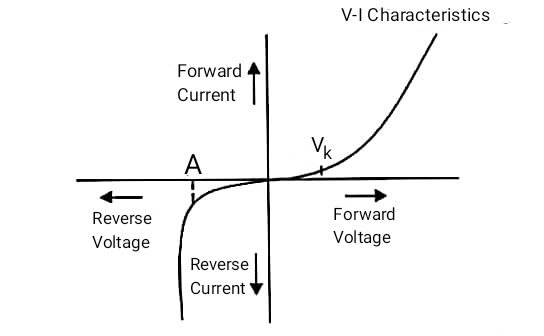
Answer – The I-V characteristics of a p–n junction diode are obtained by connecting the diode in forward bias and reverse bias as shown in the given circuits. In forward bias, the p-side of the diode is connected to the positive terminal of the battery and the n-side to the negative terminal. The milliammeter measures the forward current and the voltmeter measures the voltage across the diode. As the forward voltage increases, the current remains very small initially. When the applied voltage reaches the knee voltage , the diode starts conducting heavily and the forward current increases sharply.
In reverse bias, the p-side is connected to the negative terminal and the n-side to the positive terminal of the battery. The depletion region widens and only a very small reverse current flows, which is measured by a microammeter. This current remains almost constant and very small. As the reverse voltage increases further, the diode approaches the breakdown region where the reverse current rises suddenly.
Using the readings from both circuits, the I–V characteristic curve is plotted. The forward characteristic shows a steep rise of current after the knee voltage, while the reverse characteristic shows a very small constant reverse current (point A) until breakdown. The curve clearly shows that a p–n junction diode conducts in forward bias and offers very high resistance in reverse bias.
SECTION – E (4 Marks : CASE STUDY)
34. Electric Field Lines: Electric field lines are a way of pictorially mapping electric field around a configuration of charges. An electric field line is in general, a curve drawn in such a way that tangent to it at any point gives the direction of the net electric field at that point. An electric field line is a space curve. Relative density (i.c. closeness) of electric field lines at different points indicate the relative strength of electric field at those points. Electric field lines start from positive charge and end at negative charge. In a charge free region electric field lines may be taken to be continuous curves without any break. Electrostatic field lines do not form any closed loops.
Questions :
(i) Electric field lines about a positive point charge are :
(A) circular, anticlockwise
(B) circular, clockwise
(C) radial, inward
(D) radial, outward
Answer – (D) radial, outward
(ii) Fig. shows some of the field lines corresponding to the electric field. If EA, EB and EC be the electric fields at points A, B and C respectively, then :
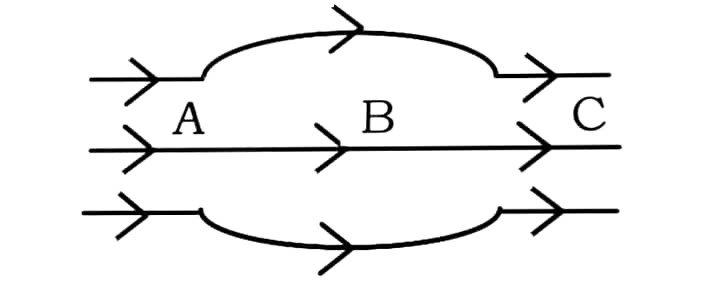
(А) ЕA > ЕB > EC
(В) ЕA = ЕB = EC
(C) ЕA = ЕC > EB
(D) ЕA = ЕC < EB
Answer – (C) ЕA = ЕC > EB
(iii) Write two properties of Electric Field Lines.
Answer – Electric field lines start from positive charge and end on negative charge, and they never intersect each other.
OR
What is Electric Field? Write its unit.
Answer – The electric field is defined as the force per unit positive charge at a point in space. Its SI unit is the volt per meter (V/m) or newton per coulomb (N/C).
35. Magnetic flux and Faraday’s Law of induction: If a magnetic field has different magnitudes and directions at various parts of a surface Fig., then the magnetic flux through the surface is given by :
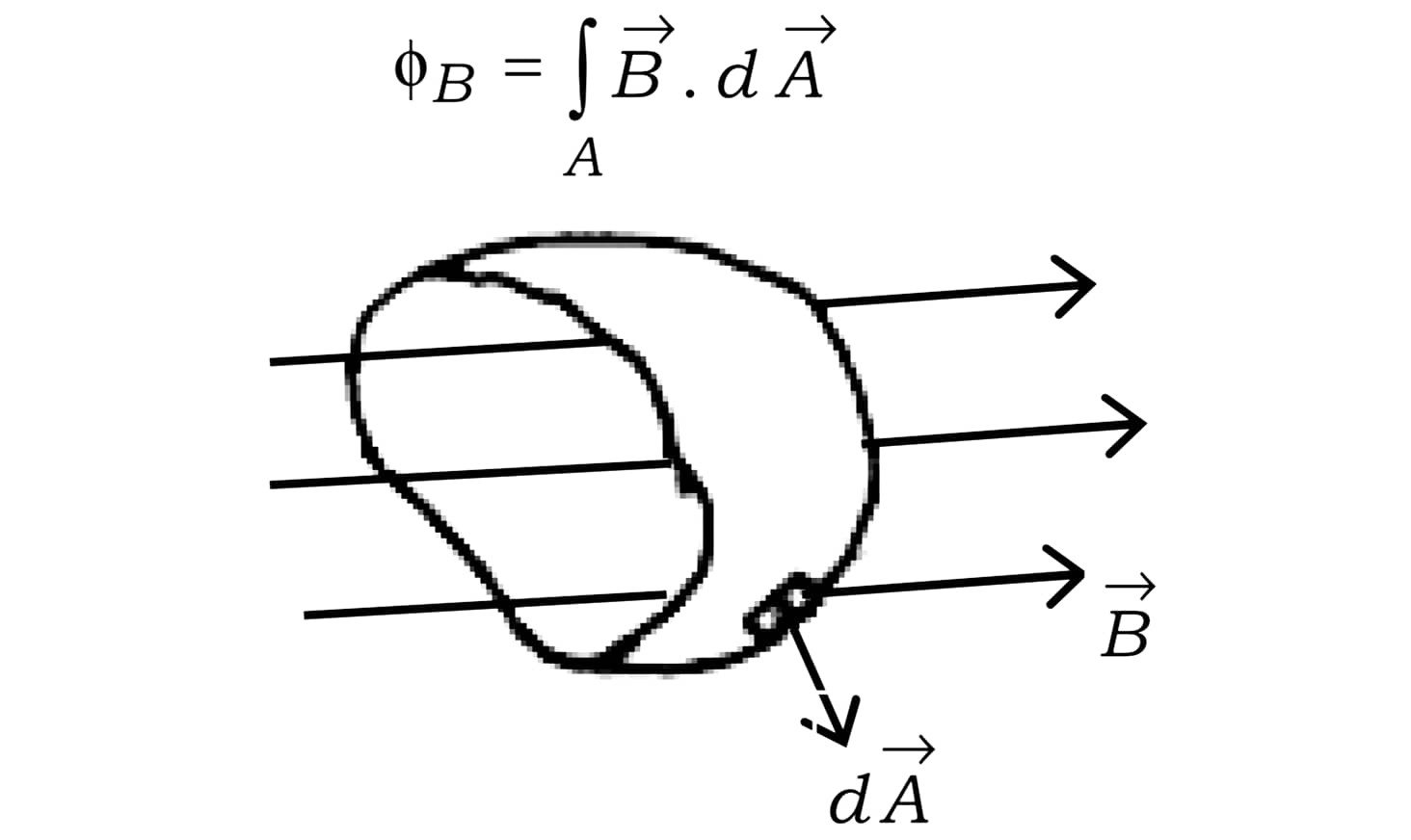
On the basis of experimental observations, Faraday concluded that an emf is induced in a coil when magnetic flux through it changes with time. Faraday stated his conclusion in the form of a law called Faraday’s law of electromagnetic induction. This law is expressed mathematically as: E = – dΦB/dt
where E is the induced emf and the negative sign indicates the direction of induced emf E and hence the direction of induced current in a closed loop. In the case of a closely wound coil of N turns, change of flux associated with each turn is the same. So the total induced emf is given by: E = – N dΦB/dt
Here ΦB is the magnetic flux associated with one turn of the coil.
Questions :
(i) SI unit of magnetic flux is :
(A) Tesla
(B) Gauss
(C) Oersted
(D) Weber
Answer – (D) Weber
(ii) PQRS is a square sheet of surface area A. A uniform magnetic field B parallel to plane of PQRS acts only in half of the region as shown in Fig. The magnetic flux linked with PQRS is :
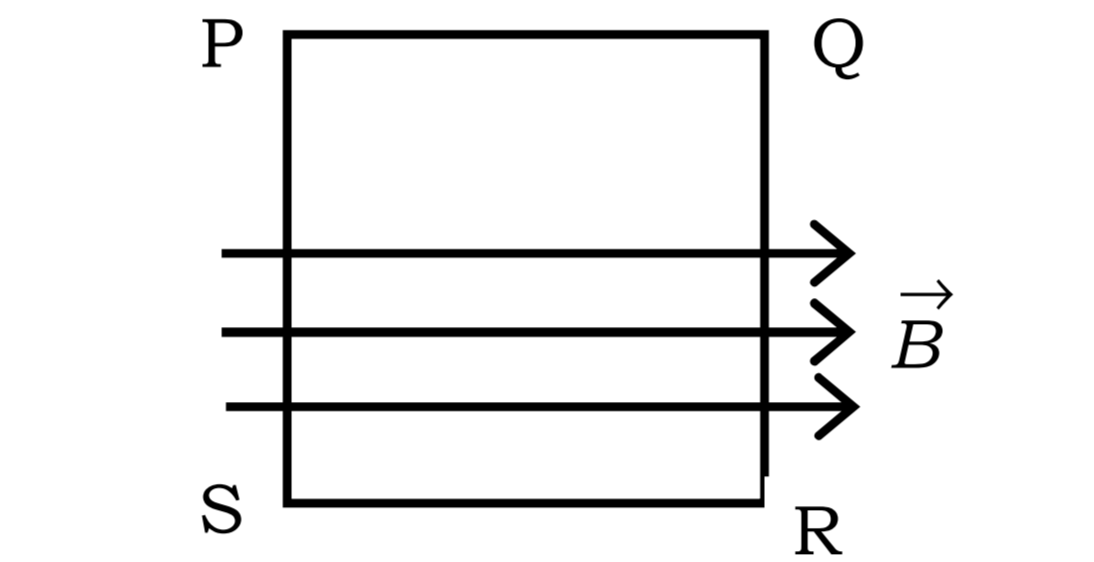
(A) 1/2 BA
(B) BA
(C) 0
(D) 2 BA
Answer – (C) 0
(iii) What is Magnetic Flux?
Answer – Magnetic flux is a measure of the total number of magnetic field lines passing normally through a given surface.
OR
An emf of 2 V is induced across the ends of 1000 turns coil. Area of each turn is 10 cm². Determine at which rate the magnetic field is changing.
Answer – Induced emf, E = 2 V
Number of turns, N = 1000
Area of each turn, A = 10 cm2 = 10 × 10–4 m2 = 10–3 m2 = 0.001 m2
Faraday’s Law, E = NA dB/dt
dB/dt = E/NA = 2/(1000×0.001) = 2 T/s
