Haryana Board (HBSE) Class 10 Maths Standard Question Paper 2024 Answer Key. BSEH (Board of School Education Haryana) Class 10 Maths Answer Key 2024. HBSE (Haryana Board of School Education) Class 10 Math Solved Question Paper 2024. BSEH Class 10 Mathematics Paper 2024 Solution. Download PDF and check accurate answers carefully prepared through my personal understanding, subject knowledge, and dedication to help students based on the syllabus and exam pattern.
HBSE Class 10 Maths (Standard) Question Paper 2024 Answer Key
SECTION – A (1 Mark)
1. 6, 72 और 120 का LCM है :
LCM of 6, 72 and 120 is :
(a) 120
(b) 6
(c) 360
(d) 240
Answer : (c) 360
6 = 2 × 3
72 = 23 × 32
120 = 23 × 3 × 5
LCM = 23 × 32 × 5 = 8 × 9 × 5 = 360
2. निम्नलिखित में से कौन-सी संख्या परिमेय है?
Which of the following is a rational number?
(a) 7 + √2
(b) 5 − √3
(c) 2 + √9
(d) 5 − √2
Answer : (c) 2 + √9
2 + √9 = 2 + 3 = 5
3. एक द्विघात बहुपद जिसके शून्यकों का योग तथा गुणनफल क्रमशः 4 और 1 है, है :
The quadratic polynomial, the sum and product of whose zeroes are 4 and 1, is :
(a) x2 − 4x – 1
(b) x2 – 4x + 1
(c) x2 + 4x – 1
(d) x2 + 4x + 1
Answer : (a) x2 − 4x + 1
Here α + β = 4, αβ = 1
Polynomial = x2 − (sum)x + product = x2 − (α + β)x + αβ = x2 − 4x + 1
4. 10, 7, 4, …… का कौन-सा पद −62 है?
Which term of A.P. 10, 7, 4, …… is −62 ?
(a) 15th
(b) 25th
(c) 27th
(d) 30th
Answer : (b) 25th
a = 10, d = 7 − 10 = −3
an = A + (n − 1)d = −62
–62 = 10 + (n − 1)(−3)
–72 = (n − 1)(–3)
n − 1 = (–72)/(–3)
n = 24 + 1 = 25
5. k का मान जिसके लिए द्विघात समीकरण kx2 – 2kx + 6 = 0 के मूल बराबर हैं :
Value of k for which the quadratic equation kx2 – 2kx + 6 = 0 has equal roots is :
(a) 6
(b) −6
(c) 8
(d) –8
Answer : (a) 6
Discriminant (D) = b2 − 4ac = 0
(–2k)2 – 4(k)(6) = 0
4k2 − 24 = 0
4k(k –6) = 0
k = 6
6. बिंदुओं (−5, 7) और (−1, 3) के बीच की दूरी है :
The distance between the points (−5, 7) and (−1, 3) is :
(a) 2√2
(b) 4√2
(c) 5√2
(d) 6√2
Answer : (b) 4√2
Distance = √[(x2–x1)2 + (y2–y1)2]
= √[(−1+5)2 + (3–7)2] = √[(4)2 + (−4)2] = √(16 + 16) = √32 = 4√2
7. त्रिभुज ABC और DEF में, ∠B = ∠E, ∠C = ∠F और AB = DE हैं, तब दो त्रिभुज हैं :
If triangles ABC and DEF, ∠B = ∠E, ∠C = ∠F and AB = DE, then the two triangles are :
(a) समरूप और सर्वांगसम / Similar aa s well as congruent
(b) सर्वांगसम लेकिन समरूप नहीं / Congruent but not similar
(c) समरूप लेकिन सर्वांगसम नहीं / Similar but not congruent
(d) न सर्वांगसम और न समरूप / Neither congruent nor similar
Answer : (a) समरूप और सर्वांगसम / Similar aa s well as congruent
8. यदि एक बिंदु P से O केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हो, तो ∠POA बराबर है :
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle 80°, then ∠POA is equal to :
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Answer : (a) 50°
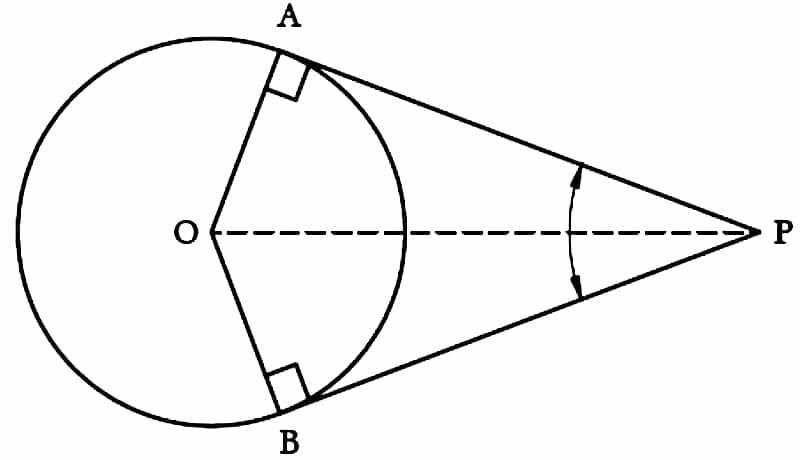
∠APB = 80°, ∠APO = 80°/2 = 40°
∠POA + ∠PAO + ∠APO = 180°
∠POA + 90° + 40° = 180°
∠POA = 180° − (90° + 40°) = 180° – 130° = 50°
9. 5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी, PQ की लंबाई है :
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm, length PQ is :
(a) 12 cm
(b) 13 cm
(c) 8 cm
(d) √119 cm
Answer : (d) √119 cm
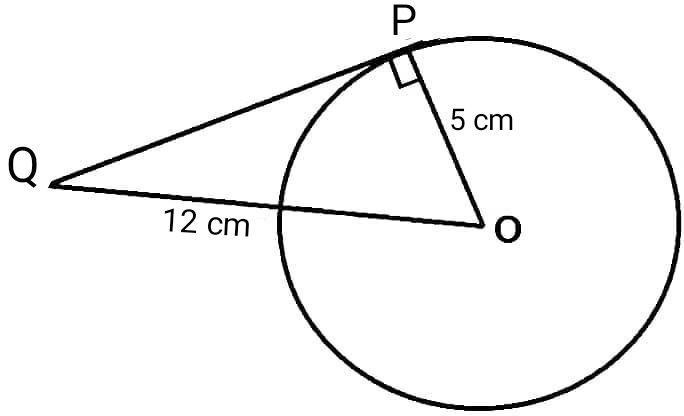
OP = radius = 5
OQ = 12
By Pythagoras: PQ2 = OQ2 − OP2 = 122 – 52 = 144 − 25 = 119
PQ = √119
10. sin60°cos30° + sin30°cos60° का मान क्या है?
What is the value of sin60°cos30° + sin30°cos60°?
(a) −1
(b) 1
(c) 0
(d) 2
Answer : (b) 1
sin60°cos30° + sin30°cos60° = √3/2 × √3/2 + 1/2 × 1/2 = 3/4 + 1/4 = 1
11. यदि sinA = 3/4, तो tan A का मान क्या है?
If sinA = 3/4, then what is the value of tanA?
(a) 3/√7
(b) 4/√7
(c) 3/5
(d) 4/5
Answer : (a) 3/√7
sinA = 3/4 = P/H
H2 = P2 + B2
B2 = H2 – P2 = 42 – 32 = 16 – 9 = 7
B = √7
tanA = P/B = 3/√7
12. 9sec2A − 9tan2A बराबर है :
9sec2A − 9tan2A is equal to :
(a) 1
(b) 9
(c) 8
(d) 0
Answer : (b) 9
9sec2A − 9tan2A = 9(sec2A − tan2A) = 9(1) = 9
13. त्रिज्या R वाले वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल जिसका कोण P° है :
Area of a sector of angle P (in degree) of a circle with radius R is :
(a) P/180 × 2πR
(b) P/180 × πR2
(c) P/360 × 2πR
(d) P/720 × 2πR2
Answer : (d) P/720 × 2πR2
Area = P/360 × πR2
14. 7 सेमी त्रिज्या R वाले एक वृत्त के त्रिज्यखण्ड का क्षेत्रफल, जिसका कोण 60° है :
The area of a sector of a circle with radius 6 cm, if angle of the sector is 60°, is :
(a) 132/7 cm2
(b) 264/7 cm2
(c) 132 cm2
(d) 64/7 cm2
Answer : (a) 132/7 cm2
Area = P/360 × πR2 = 60/360 × 22/7 × (6)2 = 132/7 cm2
15. त्रिज्या 2.1 सेमी वाले धातु के गोले का पृष्ठीय क्षेत्रफल है :
Surface area of a metallic sphere having radius 2.1 cm is :
(a) 88.7 cm2
(b) 194.5 cm2
(c) 55.44 cm2
(d) 39.04 cm2
Answer : (c) 55.44 cm2
Surface area = 4πr2 = 4 × 22/7 × (2.1)2 = 4 × 22/7 × 4.41 = 55.44 cm2
16. यदि किन्हीं आँकड़ों का माध्यक और बहुलक क्रमशः 11 और 17 हैं, तो उनका माध्य है :
If the Median and the Mode of a data are 11 and 17 respectively, then its Mean is :
(a) 7
(b) 8
(c) 9
(d) 10
Answer : (b) 8
Mode = 3 × Median − 2 × Mean
17 = 3 × 11 − 2x
17 = 33 − 2x
2x = 16
x = 8
17. निम्नलिखित वितरण के लिए, माध्य वर्ग और बहुलक वर्ग की निचली सीमाओं का योग है :
For the following distribution, the sum of lower limits of the median class and modal class is :
| Class | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
| Frequency | 10 | 15 | 12 | 20 | 9 |
(a) 15
(b) 25
(c) 30
(d) 35
Answer : (b) 25
Modal class = 15-20
Lower limit = 15
Cumulative frequency till 10-15 = 10 + 15 + 12 = 37
N = 66
N/2 = 33
Median class = 10-15
Lower limit = 10
Sum = 15 + 10 = 25
18. एक पासे को एक बार फेंका जाता है। विषम संख्या प्राप्त करने की प्रायिकता है :
A die is thrown once. The probability of getting an odd number is :
(a) 1/3
(b) 1/2
(c) 1/4
(d) 1/5
Answer : (b) 1/2
Total numbers = 6 {1, 2, 3, 4, 5, 6}
Odd numbers = 3 {1, 3, 5}
P(odd) = 3/6 = 1/2
19. अभिकथन (A) : √3 एक अपरिमेय संख्या का उदाहरण है।
कारण (R) : सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय संख्या होते हैं।
(a) अभिकथन (A) और कारण (R) दोनों सही हैं और कारण (R), अभिकथन (A) की सही व्याख्या करता है।
(b) अभिकथन (A) और कारण (R) दोनों सही हैं, लेकिन कारण (R), अभिकथन (A) की सही व्याख्या नहीं है।
(c) अभिकथन (A) सही है, लेकिन कारण (R) गलत है।
(d) अभिकथन (A) गलत है, लेकिन कारण (R) सही है।
उत्तर : (c) अभिकथन (A) सही है, लेकिन कारण (R) गलत है।
Assertion (A) : √3 is an example of an irrational number.
Reason (R) : The square roots of all positive integers are irrational numbers.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is the correct explanation of Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R) is true.
Answer : (c) Assertion (A) is true, but Reason (R) is false.
20. अभिकथन (A) : बिंदु (0, 5) y-अक्ष पर स्थित है।
कारण (R) : y-अक्ष पर किसी भी बिंदु का x-निर्देशांक शून्य होता है।
(a) अभिकथन (A) और कारण (R) दोनों सही हैं और कारण (R), अभिकथन (A) की सही व्याख्या करता है।
(b) अभिकथन (A) और कारण (R) दोनों सही हैं, लेकिन कारण (R), अभिकथन (A) की सही व्याख्या नहीं है।
(c) अभिकथन (A) सही है, लेकिन कारण (R) गलत है।
(d) अभिकथन (A) गलत है, लेकिन कारण (R) सही है।
उत्तर : (a) अभिकथन (A) और कारण (R) दोनों सही हैं और कारण (R), अभिकथन (A) की सही व्याख्या करता है।
Assertion (A) : The point (0, 5) lies on y-axis.
Reason (R) : The x-coordinate on the point on y-axis is zero.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is the correct explanation of Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R) is true.
Answer : (a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
SECTION – B (2 Marks)
21. निम्नलिखित रैखिक समीकरणों के युग्म को हल करें :
Solve the following pair of linear equations :
2x + 3y = 13
5x − 4y = −2
Answer : Given equations,
2x + 3y = 13 ……..(i)
5x − 4y = −2 ……..(ii)
Multiply eqn.(i) by 4 and eqn.(ii) by 3,
8x + 12y = 52 …….(iii)
15x − 12y = −6 …….(iv)
Add both eqn.(iii) & (iv), we get
(8x + 12y) + (15x − 12y) = 52 − 6
23x = 46
x = 2
Put x = 2 in eqn.(i),
2(2) + 3y = 13
4 + 3y = 13
3y = 9
y = 3
so, x = 2 and y = 3
22. धरती पर एक मीनार ऊर्ध्वाधर खड़ी है। धरती के एक बिंदु से, जो मीनार के पाद बिंदु से 15 m दूर है, मीनार के शिखर का उन्नयन कोण 60° है। मीनार की ऊँचाई ज्ञात कीजिए।
A tower stands vertically on the ground. From a point on the ground which is 15 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.
Answer :
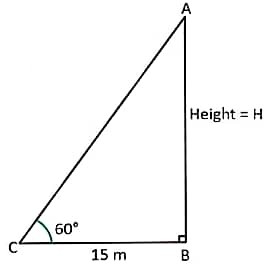
In right triangle, let height = h
tanθ = Perpendicular / Base
tan60° = h/15
√3 = h / 15
h = 15√3 m
OR
आकृति में PS/SQ = PT/TR है तथा ∠PST = ∠PRQ है। सिद्ध कीजिए कि ∆PQR एक समद्विबाहु त्रिभुज है।
In the fig. PS/SQ = PT/TR and ∠PST = ∠PRQ. Prove that ∆PQR is an isosceles triangle.

Answer : PS/SQ = PT/TR (Given)
ST || QR (by converse of BPT)
∠PST = ∠PQR (alternate angle) ……(i)
∠PST = ∠PRQ (Given) ……..(ii)
∆PST ~ ∆PRQ (by SAS similarity criterion)
∠PQR = ∠PRQ [from eqn.(i) & (ii)]
PQ = PR
Triangle PQR has two equal sides. It is isosceles.
23. एक बिंदु A से जो वृत्त के केंद्र से 5 cm की दूरी पर है, वृत्त पर स्पर्शरेखा की लंबाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
The length of a tangent from a point A at distance 5 cm from the centre of a circle is 4 cm. Find the radius of circle.
Answer :
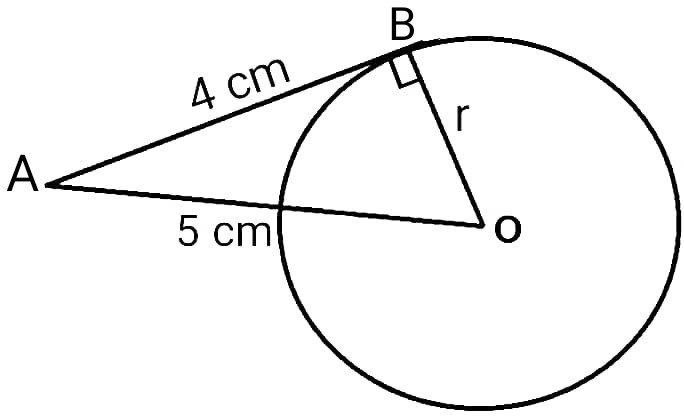
Here AO = 5 cm, AB = 4 cm, ∠ABO = 90° (BO ⊥ AB)
Using Pythagoras theorem, H2 = P2 + B2
AO2 = AB2 + BO2
BO2 = AO2 – AB2
BO2 = 52 – 42
BO2 = 25 – 16
BO2 = 9
BO = √9
BO = 3 cm
Radius of circle (BO) = 3 cm
24. निम्नलिखित का मान ज्ञात कीजिए :
Evaluate the following :
2tan245° + cos230° – sin260°
Answer : 2tan245° + cos230° – sin260°
= 2(1)2 + (√3/2)2 – (√3/2)2
= 2(1) + (3/4) – (3/4)
= 2
25. त्रिज्या 4 cm वाले एक वृत्त के त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 30° है।
Find the area of the sector of a circle with radius 4 cm and angle 30°.
Answer : Area = θ/360 × πr2 = 30/360 × 22/7 × 42 = 88/21 = 4.19 cm2
OR
एक वृत्त के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है।
Find the area of a quadrant of a circle, whose circumference is 22 cm.
Answer : Circumference = 2πr = 22
r = 22 ÷ (2 × 22/7) = 7/2 = 3.5 cm
Quadrant area = 1/4 × πr2 = 1/4 × 22/7 × (3.5)2 = 77/8 = 9.63 cm2
SECTION – C (3 Marks)
26. सिद्ध कीजिए कि √5 एक अपूर्णांक संख्या है।
Prove that √5 is an irrational number.
Answer : Let us assume that √5 is a rational number.
Now √5 = p/q where p and q are co-prime integers and q ≠ 0
p = √5q
Squaring both sides, we get
p2 = 5q2 ……..(i)
5 divides p2, then 5 also divides p
Put p = 5m in eqn.(i),
(5m)2 = 5q2
25m2 = 5q2
5m2 = q2
5 divides q2 then 5 also divides q
Here p, q have a common factor is 5. This contradicts our assumption that they are co-primes. Therefore, p/q is not a rational number
Hence √5 is an irrational number.
27. द्विघात बहुपद x2 + 7x + 10 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए।
Find the zeroes of quadratic polynomial x2 + 7x + 10 and verify the relationship between the zeroes and the coefficients.
Answer : Compare x2 + 7x + 10 with ax2 + bx + c
Here a = 1, b = 7, c = 10
x2 + 7x + 10 = 0
x2 + 5x + 2x + 10 = 0
x(x + 5) + 2(x + 5) = 0
(x + 5)(x + 2) = 0
x = –5, –2
so, α = –5 and β = –2
α + β = – 5 – 2 = – 7 = –b/a = (–7)/1 = – 7
αβ = (–5)(–2) = 10 = c/a = 10/1 = 10
Thus, the basic relationships are verified.
28. दो व्यक्तियों की आय का अनुपात 9 : 7 है और उनके खर्चों का अनुपात 4 : 3 है। यदि प्रत्येक व्यक्ति प्रति महीने 2,000 रुपया बचा लेता है, तो उनकी मासिक आय ज्ञात कीजिए।
The ratio of incomes of two persons is 9 : 7 and the ratio of their expenditures is 4 : 3. If each of them manages to save Rs. 2000 per month, find their monthly income.
Answer :
Let the two persons be A and B.
Let incomes be 9x and 7x
Let expenses be 4y and 3y
ATQ,
9x − 4y = 2000 ……(i)
7x − 3y = 2000 …….(ii)
Multiply eqn.(i) by 3 and eqn.(ii) by 4,
27x − 12y = 6000 ……..(iii)
28x − 12y = 8000 ……..(iv)
Subtract eqn.(iii) from eqn.(iv), we get
x = 2000
Income of A = 9x = 9(2000) = ₹ 18000
Income of B = 7x = 7(2000) = ₹ 14000
OR
दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18° अधिक है। उन्हें ज्ञात कीजिए।
The larger of two supplementary angles exceeds the smaller by 18°. Find them.
Answer : Let smaller angle = x
Then larger angle = x + 18°
Supplementary = x + x + 18 = 180°
2x = 162
x = 81
Smaller angle = x = 81°
Larger angle = x + 18 = 81 + 18 = 99°
29. सिद्ध कीजिए कि दो संकेन्द्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिंदु पर समद्विभाजित होती है।
Prove that in two concentric circles the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
Answer :
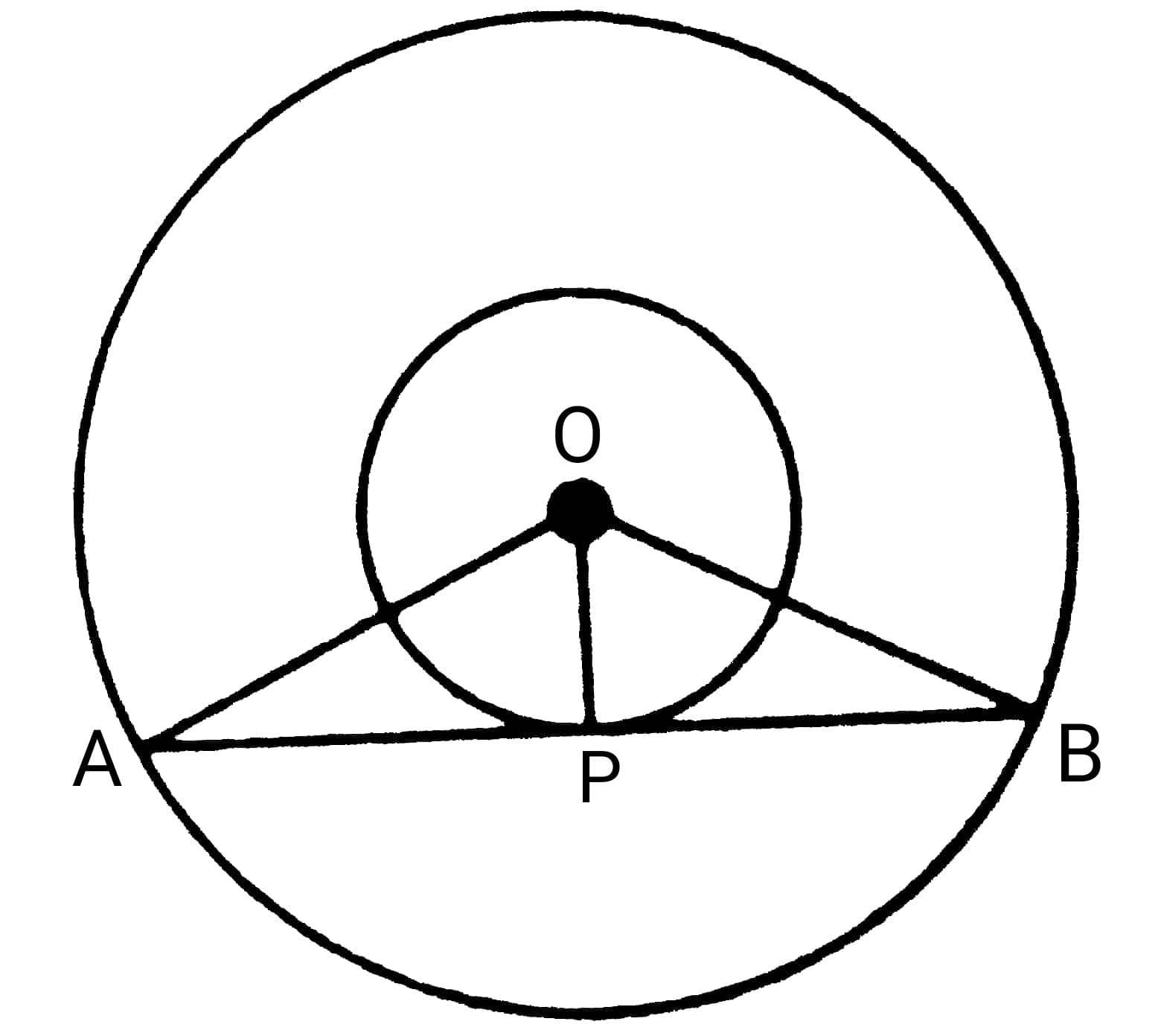
Let O be the common centre, AB a chord of the larger circle, touching the smaller circle at point P. Since AB is tangent to the smaller circle at P and O is the centre,
∠APO = ∠BPO (OP ⊥ AB)
OA = OB (Radii)
OP = OP (Common)
∆APO ≅ ∆BPO (by RHS rule)
Hence, AP = BP (CPCT)
30. सिद्ध कीजिए :
Prove that :
√[(1+sinA)/(1–sinA)] = secA + tanA
Answer : LHS = √[(1+sinA)/(1–sinA)]
Rationalise the denominator,
= √[(1+sinA)/(1–sinA)] × √[(1+sinA)/(1+sinA)]
= √[(1+sinA)2/(1–sin2A)]
= √[(1+sinA)2/cos2A]
= (1+sinA)/cosA
= 1/cosA + sinA/cosA
= secA + tanA = RHS
OR
सिद्ध कीजिए :
Prove that :
secA(1 – sinA)(secA + tanA) = 1
Answer : LHS = secA(1 – sinA)(secA + tanA)
= 1/cosA (1 – sinA)(1/cosA + sinA/cosA)
= 1/cosA (1 – sinA)(1 + sinA)/cosA
= (12 – sin2A) / cos2A
= cos2A/cos2A
= 1 = RHS
31. एक पासे को एक बार फेंका जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए :
(i) एक अभाज्य संख्या
(ii) 2 और 6 के बीच स्थित कोई संख्या
(iii) एक विषम संख्या
A die is thrown once, find the probability of getting :
(i) a prime number
(ii) a number lying between 2 and 6
(iii) an odd number
Answer : Total numbers = 6 {1, 2, 3, 4, 5, 6}
(i) Prime numbers = 3 {2, 3, 5}
P = 3/6 = 1/2
(ii) Numbers between 2 and 6 = 3 {3, 4, 5}
P = 3/6 = 1/2
(iii) Odd numbers = 3 {1, 3, 5}
P = 3/6 = 1/2
SECTION – D (5 Marks)
32. दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए, जिनके वर्गों का योग 365 है।
Find two consecutive positive integers, sum of whose squares is 365.
Answer : Let the two consecutive integers be x and x + 1.
Then, x2 + (x + 1)2 = 365
x2 + x2 + 2x + 1 = 365
2x2 + 2x + 1 = 365
2x2 + 2x − 364 = 0
Divide by 2,
x2 + x − 182 = 0
x2 + 14x – 13x – 182 = 0
x(x + 14) – 13(x + 14) = 0
(x + 14)(x – 13) = 0
x = 13 (reject x = –14)
x + 1 = 13 + 1 = 14
so, numbers are 13 and 14.
OR
समीकरण 3x2 – 2x + 1/3 = 0 का विविक्तकर ज्ञात कीजिए और फिर मूलों की प्रकृति ज्ञात कीजिए। यदि वे वास्तविक हैं, तो उन्हें ज्ञात कीजिए।
Find the discriminant of the equation 3x2 – 2x + 1/3 = 0 and hence find the nature of its roots. Find them, if they are real.
Answer : 3x2 – 2x + 1/3 = 0
Multiply both sides by 3,
9x2 − 6x + 1 = 0
Compare 9x2 − 6x + 1 = 0 with ax2 + bx + c
Here a = 9, b = –6, c = 1
Discriminant D = b2 − 4ac = (−6)2 − (4)(9)(1) = 36 – 36 = 0
The given equation has two equal real roots.
9x2 − 6x + 1 = 0
9x2 – 3x – 3x + 1 = 0
3x(3x – 1) – 1(3x – 1) = 0
(3x – 1)(3x – 1) = 0
x = 1/3, 1/3
33. 90 cm की लंबाई वाली एक लड़की बल्ब लगे एक खंभे के आधार से परे 1.2 m/s की चाल से चल रही है। यदि बल्ब भूमि से 3.6 m की ऊँचाई पर है, तो 4 सेकण्ड बाद उस लड़की की छाया की लंबाई ज्ञात कीजिए।
A girl of height 90 cm is walking away from the base of a lamp post at the speed of 1.2 m/s. If the lamp is 3.6 m above the ground. Find the length of her shadow after 4 second.
Answer :
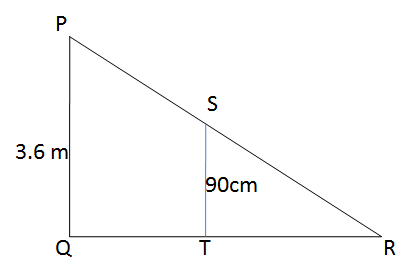
Height of lamp, PQ = 3.6 m
Height of girl, ST = 90 cm = 0.9 m
Distance moved, QT = speed × time = 1.2 × 4 = 4.8 m
Let length of shadow, TR = x
Using similar triangles,
Height of lamp / Total shadow = Height of girl / Length of shadow
PQ / QR = ST / TR
3.6 / (4.8 + x) = 0.9 / x
3.6x = 0.9(4.8 + x)
3.6x = 4.32 + 0.9x
2.7x = 4.32
x = 4.32 / 2.7 = 1.6 m
Length of shadow = 1.6 m
34. शांता किसी शेड (shed) में एक उद्योग चलाती है। यह शेड एक घनाभ के आकार का है जिस पर एक अर्ध-बेलन आरोपित है। यदि इस शेड के आधार की विमाएँ 7 m × 15 m है, तो घनाभाकार भाग की ऊँचाई 8 m है, तो शेड में समावेशित हो सकने वाली हवा का आयतन ज्ञात कीजिए। पुनः यदि मान लें कि शेड में रखी मशीनरी 300 m3 स्थान घेरती है और शेड के अन्दर 20 श्रमिक हैं जिनमें से प्रत्येक 0.08 m3 के औसत से स्थान घेरता है, तब शेड में कितनी हवा होगी? (π = 22/7 लीजिए)
Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder. If the base of the shed is of dimension 7 m × 15 m and the height of the cuboidal portion is 8 m. Find the volume of air that shed can hold. Further suppose the machinery in the shed occupies a total space of 300 m3 and there are 20 workers, each of whom occupy about 0.08 m3 space on an average. Then how much air is in the shed? (Take π = 22/7)
Answer :
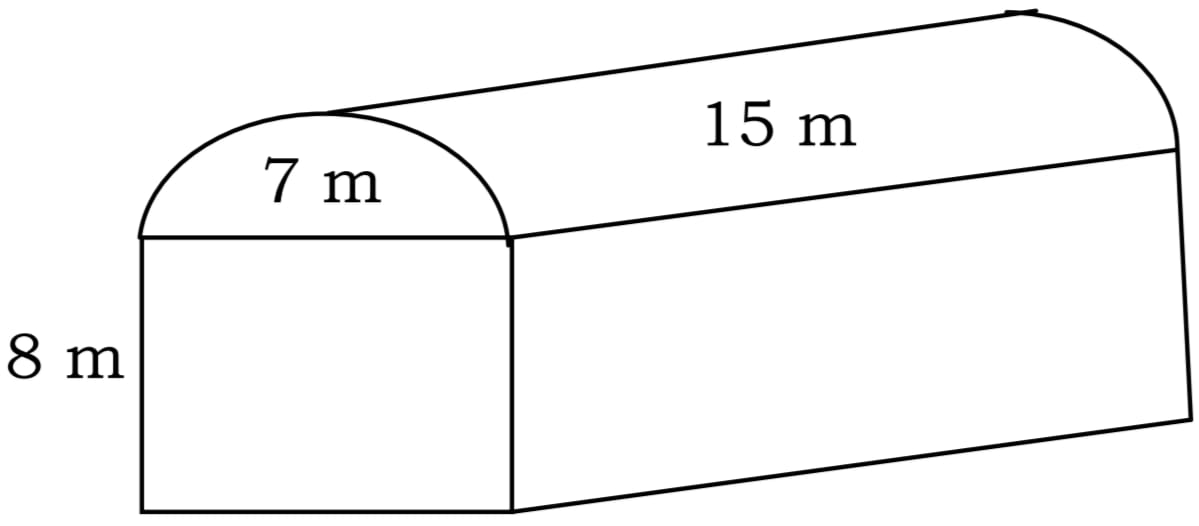
Volume of air in the shed = volume of cuboid + volume of half cylinder = (L × B × H) + πr2h/2 = (15 × 7 × 8) + 22/7 × (3.5)2 × 15 = 840 + 412.5 = 1252.5 m3
Machine occupy space = 300 m3
Workers occupy space = 20 × 0.08 = 1.6 m3
Occupied space = 300 + 1.6 = 301.6 m3
Remaining air in shed = 1252.5 − 301.6 = 950.9 m3
OR
आकृति में दर्शाया गया सजावट के लिए प्रयोग होने वाले ब्लॉक दो ठोसों से मिलकर बना है। इसमें से एक घन है और दूसरा अर्धगोला है। इस ब्लॉक का आधार 5 cm कोर या किनारे वाला एक घन है और ऊपरी लगे हुए अर्थगोले का व्यास 4.2 cm है। इस ब्लॉक का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 22/7 लीजिए)
The decorative block shown in fig. is made of two solids – a cube and a hemisphere. The base of the block is a cube with edge 5 cm and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Take π = 22/7)
Answer :
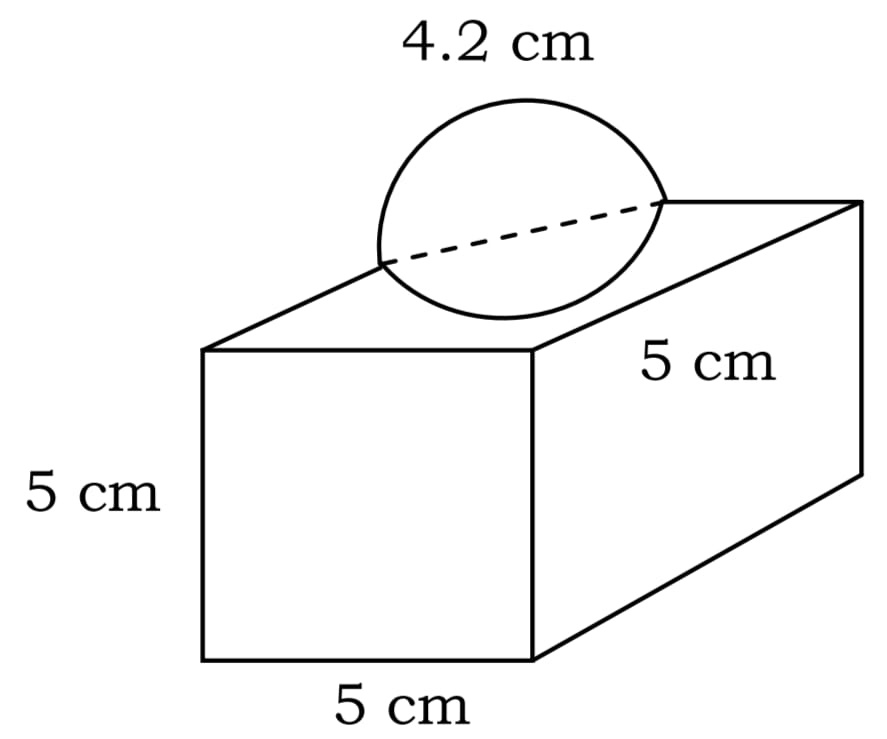
Radius of hemisphere = 4.2 / 2 = 2.1 cm
Total surface area of block = Total surface area of cube + curved surface area of hemisphere – base area of hemisphere
= 6a2 + 2πr2 – πr2 = 6a2 + πr2 = 6(5)2 + 22/7 × (2.1)2 = 150 + 13.86 = 163.86 cm2
35. निम्नलिखित बारंबारता बंटन किसी मोहल्ले के 68 उपभोक्ताओं की बिजली की मासिक खपत दर्शाता है। इन आँकड़ों के लिए बहुलक ज्ञात कीजिए :
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the mode of data :
| Monthly Consumption (in Units) | No. of Consumers |
| 65-85 | 4 |
| 85-105 | 5 |
| 105-125 | 13 |
| 125-145 | 20 |
| 145-165 | 14 |
| 165-185 | 8 |
| 185-205 | 4 |
Answer : From the table, it can be observed that the maximum class frequency is 20, belonging to class interval 125-145.
Modal class = 125-145
Class size, h = 20
Lower limit of modal class, l = 125
Frequency of modal class, f1 = 20
Frequency of class preceding modal class, f0 = 13
Frequency of class succeeding the modal class, f2 = 14
Mode = l + [(f1 – f0)/(2f1 – f0 – f2)] × h
= 125 + [(20 – 13)/(2 × 20 – 13 – 14)] × 20
= 125 + [7/(40 – 27)] × 20
= 125 + (7/13) × 20
= 125 + 140/13
= 125 + 10.76
= 135.76
SECTION – E (4 Marks : CASE STUDY)
36. टी०वी० सेटों का निर्माता तीसरे वर्ष में 600 टी०वी० तथा 7वें वर्ष में 700 टी०वी० सेटों का उत्पादन करता है। यह मानते हुए कि प्रत्येक वर्ष उत्पादन में एक समान रूप से निश्चित संख्या में वृद्धि होती है, ज्ञात कीजिए :
A manufacturer of TV sets produced 600 sets in third year and 700 sets in seventh years. Assuming that the production increase uniformly by a fixed number every year, find :
(i) प्रथम वर्ष में उत्पादन
the production in the 1st year
Answer : an = a + (n – 1)d
3rd year production, a + 2d = 600 ……..(i)
7th year production, a + 6d = 700 ……..(ii)
Subtract eqn.(i) from (ii), we get
4d = 100
d = 100/4 = 25
Put d = 25 in eqn.(i),
a + 2(25) = 600
a = 600 – 50 = 550
so, the production in the 1st year is 550.
(ii) 10वें वर्ष में उत्पादन
the production in 10th year
Answer : a10 = a + 9d = 550 + 9(25) = 550 + 225 = 775
so, the production in 10th year is 775.
(iii) (a) प्रथम 7 वर्षों में कुल उत्पादन
the total production in first 7 years
Answer : Sn = n/2 [2a + (n – 1)d]
S7 = 7/2 [2(550) + 6(25)] = 7/2 [1100 + 150] = 7/2 × 1250 = 4375
so, the total production in first 7 years is 4375.
OR
(b) 10 वर्षों में कुल उत्पादन
total production in 10 years
Answer : Sn = n/2 [2a + (n – 1)d]
S10 = 10/2 [2(550) + 9(25)] = 5 × [1100 + 225] = 5 × 1350 = 6625
so, the total production in first 10 years is 6625.
37. एक सोसाइटी के रेजिडेंट वेलफेयर एसोसिएशन (RWA) ने एक सोसाइटी के पार्क में तीन बिजली के खंभे A, B और C लगाए। इन तीन खंभों के बावजूद, पार्क के कुछ हिस्सों में अभी भी अंधेरा है इसलिए RWA एक और बिजली का खंभा D लगाने का फैसला किया। उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दें :
Resident Welfare Association (RWA) of a society put up three electric poles A, B and C in a society’s park. Despite these three poles, some part of the park are still in dark, so RWA decides to have one more electric pole D in the park.Based on the above information, answer the following questions :
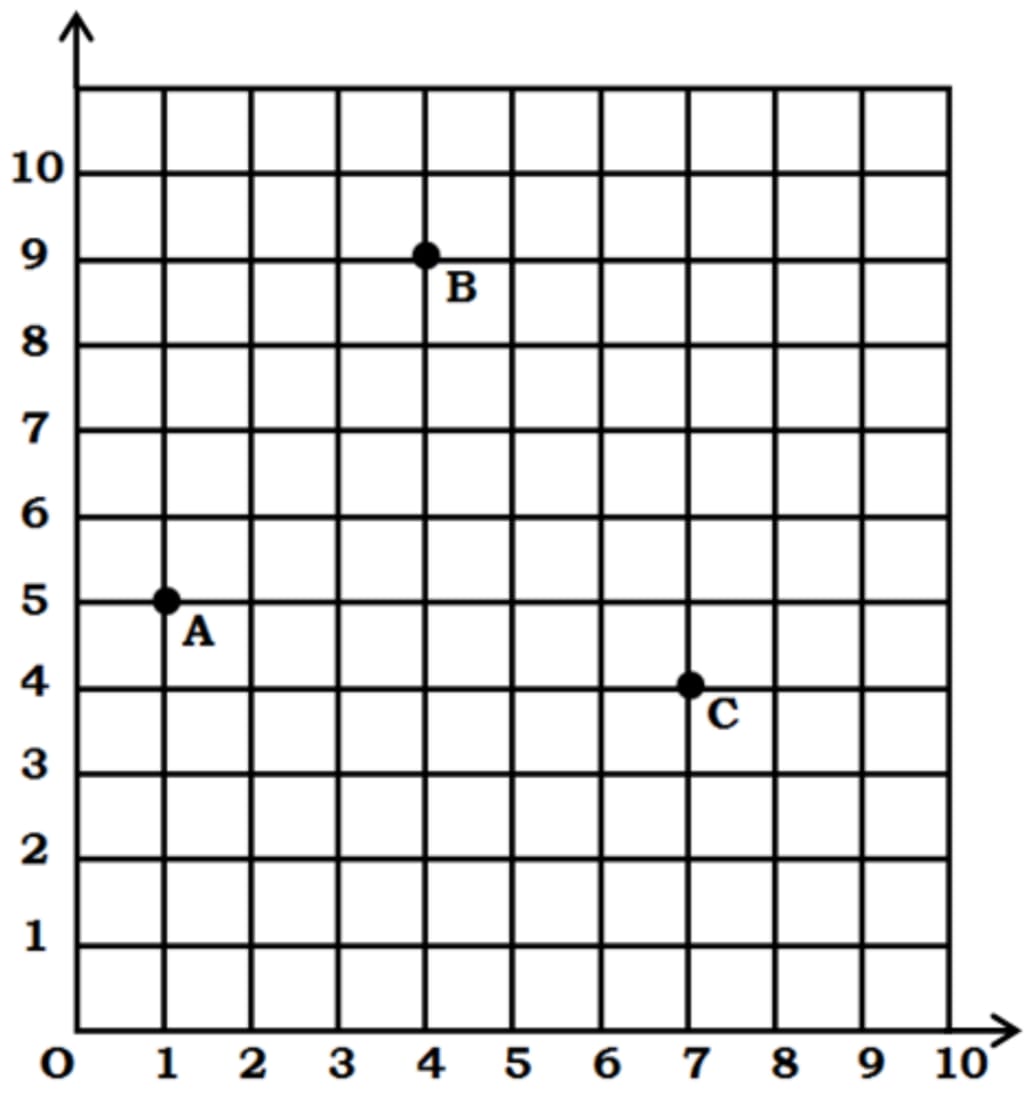
(i) खंभे C की स्थिति ज्ञात कीजिए।
Find the position of the pole C.
Answer : Coordinates of pole C = (7, 4)
(ii) पार्क के कोने O से खंभे B की दूरी ज्ञात कीजिए।
Find the distance of the pole B from corner O of the park.
Answer : O(0, 0) and B(4, 9)
Distance = √[(x2–x1)2 + (y2–y1)2]
= √[(4–0)2 + (9–0)2] = √[(4)2 + (9)2] = √(16 + 81) = √97 unit
(iii) (a) चौथे खंभे D की स्थिति ज्ञात कीजिए, ताकि चार बिंदु A, B, C और D एक समांतर चतुर्भुज बना लें।
Find the position of the fourth pole D so that four points A, B, C and D form a parallelogram.
Answer : A(1, 5), B(4, 9) ,C(7, 4) are three vertices of parallelogram ABCD and let D(x, y) be the fourth vertex
Mid point of diagonal AC = Mid point of diagonal BD
[(7+1)/2, (5+4)/2] = [(x+4)/2, (9+y)/2]
x = 4, y = 0
D(4, 0)
OR
(b) खंभों A और C के बीच की दूरी ज्ञात कीजिए।
Find the distance between poles A and C.
Answer : A(1, 5) and B(7, 4)
Distance = √[(x2–x1)2 + (y₂–y₁)2]
= √[(7–1)2 + (4–5)2] = √[(6)2 + (–1)2] = √(36 + 1) = √37 unit
38. सड़क के दोनों ओर खड़े समान ऊँचाई के दो खंभों पर दो होर्डिंग लगाए जाते हैं। सड़क पर उनके बीच एक बिंदु से खंभों के शीर्ष का उन्नयन कोण क्रमशः 60° और 30° है। प्रत्येक खंभे की ऊँचाई 20 मीटर है। उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए :
Two hoardings are put on two poles of equal heights standing on either side of the road. From a point between them on the road the angle of elevation of the top of poles are 60° and 30° respectively. Height of each of pole is 20 m. Basis of above information, answer the following questions :
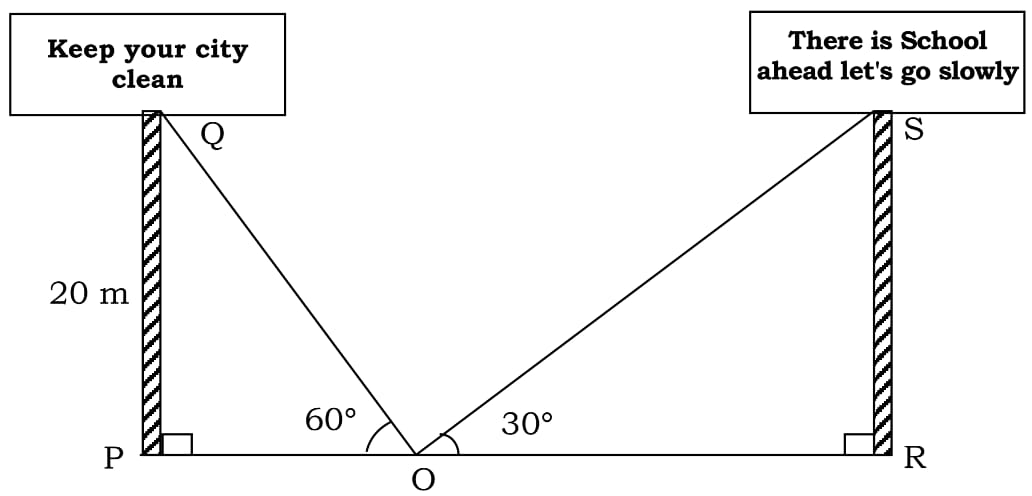
(i) PO की लंबाई ज्ञात कीजिए।
Find the length of PO.
Answer : tanθ = Perpendicular / Base
tan60° = 20 / PO
√3 = 20 / PO
PO = 20 / √3 = 20/√3 × √3/√3 = (20√3)/3 m
(ii) RO की लंबाई ज्ञात कीजिए।
Find the length of RO.
Answer : tanθ = Perpendicular / Base
tan30° = 20 / RO
1/√3 = 20 / RO
RO = 20√3 m
(iii) (a) सड़क की चौड़ाई ज्ञात कीजिए।
Find the width of the road.
Answer : Width of road = PO + RO = (20√3)/3 + (20√3) = (80√3)/3 m
OR
(b) यदि खंभे PQ द्वारा बनाया गया उन्नयन कोण 45° है, तो PO की लंबाई ज्ञात कीजिए।
If the angle of elevation made by PQ is 45°, then find the length of PO.
Answer : tanθ = Perpendicular / Base
tan45° = 20 / PO
PO = 20 m
