Haryana Board (HBSE) Class 10 Maths SAT-1 Question Paper 2025 Answer Key. Get the Students Assessment Test (SAT) Class 10 Maths question paper with complete solution, accurate answer key, and expert preparation tips. The Haryana Board of School Education (HBSE) conducts SAT as an important assessment for Class 10 students. Best resource for Haryana Board Class 10 SAT Mathematics exam practice, quick revision, and scoring better marks.
HBSE Class 10 Maths SAT-1 Question Paper 2025 Answer Key
Instructions :
• All questions are compulsory.
• Questions (1-11) carry 1 mark each.
• Questions (12-14) carry 2 marks each.
• Questions (15-17) carry 3 marks each.
• Questions (18-19) carry 5 marks each.
• Question (20) case study, carry 4 marks.
1. निम्नलिखित में से कौन-सी अपरिमेय संख्या नहीं है?
Which of the following is not an irrational number?
(A) 3 + √2
(B) 5 – √5
(C) 3 + √16
(D) 4 – √8
Answer : (C) 3 + √16
2. द्विघात बहुपद x2 – 4x + 1 के शून्यकों का योगफल है :
Sum of zeros of quadratic Polynomial x2 – 4x + 1 is :
(A) 4
(B) – 4
(C) 1
(D) – 1
Answer : (A) 4
α + β = – b/a = – (–4)/1 = 4
3. रैखिक समीकरणों के युग्म 2x + 4y – 8 = 0 तथा 5x + 10y – 20 = 0 का हल होगा :
The Pair of linear equations 2x + 4y – 8 = 0 and 5x + 10y – 20 = 0 has solution :
(A) Unique solution
(b) No Solution
(C) Infinitely many solution
(D) None of these
Answer : (C) Infinitely many solution
a1/a2 = b1/b2 = c1/c2 = 2/5
4. निम्नलिखित में से कौन-सी घटना की प्रायिकता नहीं हो सकती है?
Which of the following cannot be the Probability of an event?
(A) 1
(B) – 1.5
(C) 15%
(D) 0.7
Answer : (B) – 1.5
5. प्रथम पाँच प्राकृत संख्याओं का माध्य होगा :
The mean of the first five natural numbers will be :
(A) 3
(B) 5
(C) 15
(D) None of these
Answer : (A) 3
Mean = (1+2+3+4+5)/5 = 15/5 = 3
6. द्विघात समीकरण x2 + x – 1 के मूलों की प्रकृति होगी :
The nature of roots of the quadratic equation x2 + x – 1 will be :
(A) Real and Unequal
(B) Real and equal
(C) Unreal
(D) None of these
Answer : (A) Real and Unequal
Discriminant (D) = b² – 4ac = (1)2 – 4(1)(–1) = 1 + 4 = 5
D > 0
7. द्विघात समीकरण x2 – 5x + 6 = 0 का विवित्तकर ………….. है।
The Discriminant of quadratic equation x2 – 5x + 6 = 0 is …………
Answer : Discriminant (D) = b2 – 4ac = (–5)2 – 4(1)(6) = 25 – 24 = 1
8. किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग …………… होता है।
The sum of probabilities of all the elementary events of an experiment is ………….
Answer : 1
9. वर्ग अंतराल 30-40 का वर्ग चिन्ह क्या होगा?
What is the class mark of the class Interval 30-40?
Answer : Class mark = (30+40)/2 = 70/2 = 35
10. संख्या 270 को अभाज्य गुणनखंड के रूप में व्यक्त कीजिए।
Express 270 as a product of its Prime factors.
Answer : 270 = 2 × 3 × 3 × 3 × 5 = 21 × 33 × 51
11. अभिकथन (A) : y2 – 5 एक द्विघात बहुपद है।
तर्क (R) : दो घात वाले बहुपद को द्विघात बहुपद कहते हैं।
Assertion (A) : y2 – 5 is a quadratic polynomial.
Reason (R) : A polynomial of degree two is called a quadratic polynomial.
(a) Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer : (a) Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct explanation of Assertion (A).
12. द्विघात बहुपद 3x2 – x – 4 के शून्यक ज्ञात करें और शून्यकों और गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच करें।
Find the zeros of the quadratic polynomial 3x2 – x – 4 and verify the relationship between the zeros and their coefficients.
Answer : Compare 3x2 – x – 4 with ax2 + bx + c
Here a = 3, b = – 1, c = – 4
3x2 – x – 4 = 0
3x2 – 4x + 3x – 4 = 0
x(3x – 4) + 1(3x – 4) = 0
(3x – 4)(x + 1) = 0
x = 4/3, –1
α = 4/3 and β = –1
α + β = 4/3 – 1 = 1/3 = – b/a = – (–1)/3 = 1/3
αβ = (4/3)(–1) = – 4/3 = c/a = – 4/3
Thus, the basic relationships are verified.
13. निम्नलिखित रैखिक समीकरण युग्म को हल कीजिए।
Solve the following pair of linear equations.
x – y = 3, x/3 + y/2 = 6
Answer : Given pair of linear equations,
x – y = 3 ……..(i)
x/3 + y/2 = 6 ……….(ii)
Multiply eqn.(i) by 3, eqn.(ii) by 6, we get
3x – 3y = 9 ………(iii)
2x + 3y = 36 ………(iv)
Add eqn.(iii) and (iv), we get
5x = 45
x = 9
Put x = 9 in eqn.(i), we get
y = 9 – 3 = 6
Therefore x = 9 and y = 6
14. k के किस मान के लिए द्विघात समीकरण 2x2 + kx + 3 = 0 के मूल बराबर होंगे।
For what value of k, the quadratic equation 2x2 + kx + 3 = 0 has equal roots?
Answer : Here, a = 2, b = k, c = 3
Discriminant (D) = b2 – 4ac = 0
k2 – 4(2)(3) = 0
k2 – 24 = 0
k2 = 24
k = √24
k = ± 2√6
15. सिद्ध कीजिए कि √5 एक अपरिमेय संख्या है।
Prove that √5 is irrational.
Answer :
Answer : Let us assume that √5 is a rational number.
Now, √5 = p/q where p and q are co-prime integers and q ≠ 0
p = √5q
Squaring both sides, we get
p2 = 5q2 ……..(i)
5 divides p2, then 5 also divides p
Put, p = 5m in eqn.(i),
(5m)2 = 5q2
25m2 = 5q2
5m2 = q2 (Divide both side by 5)
5 divides q2 then 5 also divides q
Hence p, q have a common factor is 5 . This contradicts our assumption that they are co-primes. Therefore, p/q is not a rational number
Hence √5 is an irrational number.
16. 5 वर्ष बाद, जैकब की आयु उसके पुत्र की आयु से तीन गुनी हो जायेगी। 5 वर्ष पूर्व, जैकब की आयु उसके पुत्र की आयु की सात गुनी थी। उनकी वर्तमान आयु क्या है?
Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times of his son. What are their present ages?
Answer : Let the present age of Jacob = x
And, the present age of Son = y
5 years hence, age of Jacob = x + 5
5 years hence, age of Son = y + 5
ATQ,
x + 5 = 3(y + 5)
x + 5 = 3y + 15
x – 3y = 10 ……….(i)
5 years ago, age of Jacob = x – 5
10 years later, age of Sonu = y – 5
ATQ,
x – 5 = 7(y – 5)
x – 5 = 7y – 35
x – 7y = – 30 ……….(ii)
Subtract eqn.(i) from eqn.(ii), we get
– 4y = – 40
y = 10
Put y = 10 in eqn.(i),
x – 3(10) = 10
x – 30 = 10
x = 10 + 30 = 40
Hence, the age of Jacob (x) = 40 years and age of Son (y) = 10 years.
17. 52 पत्तों की अच्छी प्रकार से फैटी गई एक गड्डी में से एक पत्ता निकाला जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए :
If one card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting :
(i) a queen of red colour
(ii) a face card
(iii) 2 of hearts
Answer :
(i) No. of queen of red colour = 2
P(E) = 2/52 = 1/26
(ii) No. of face cards = 12
P(E) = 12/52 = 3/13
(iii) No. of 2 of heart = 1
P(E) = 1/52
18. एक रेलगाड़ी 360 किमी/घंटा की एक समान चाल से चलती है। यदि उसकी चाल 5 किमी/घंटा बढ़ा दी जाये तो वह 1 घंटे कम में यात्रा पूरी कर लेती है। रेलगाड़ी की चाल जात कीजिए।
A train travels 360 km/h at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Answer : Let the speed of the train be x km/h and the time taken be t hours.
Distance = Speed × Time
360 = x × t
t = 360/x
Increased speed of the train can be written as (s + 5)
t = 360/(x + 5)
ATQ,
360/x – 360/(x + 5) = 1
x2 + 5x – 1800 = 0
x2 + 45x – 40x – 1800 = 0
x(x + 45) – 40(x + 45) = 0
(x + 45)(x – 40) = 0
x = 40 (x ≠ – 45 speed not negative)
The speed of the train is 40 km/h.
19. दो वर्गों के क्षेत्रफलों का योग 468 m2 है। यदि उनके परिमापों का अंतर 24 m हो, तो दोनों वर्गों की भुजाएं ज्ञात करे।
The sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, then find the sides of the two squares.
Answer : Let the sides of the two squares be x and y
The area of squares are x2 and y2
ATQ,
x2 + y2 = 468 ……….(i)
4x – 4y = 24
x – y = 6
x = y + 6 ………..(ii)
Put x = y + 6 in equ.(i), we get
(y + 6)2 + y2 = 468
y2 + 12y + 36 + y2 = 468
2y2 + 12y – 432 = 0
y2 + 6y – 216 = 0
y2 + 18y – 12y – 216 = 0
y(y + 18) – 12(y + 18) = 0
(y + 18)(y – 12) = 0
y = 12 (y ≠ – 18 length not negative)
Put y = 12 in eqn.(ii),
x = 12 + 6 = 18
Therefore, the sides of the two squares are 18 m and 12 m.
20. CASE STUDY : एक कक्षा में 4 दोस्त राम, राजन, प्रवीण और रमन चित्र में दिखाए अनुसार बिन्दु A, B, C और D पर बैठे हैं। यह मानते हुए कि O मूल बिन्दु है। आकृति का अवलोकन करें और आकृति के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए :
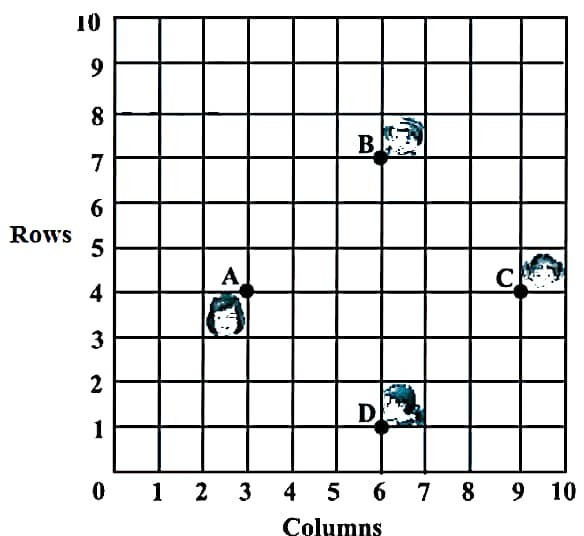
In a classroom 4 friends Ram, Rajan, Praveen and Raman are sitting on the points A, B, C and D as shown in the fig. Assuming O be the origin.
Observe the figure and answer the following questions based on the figure :
(i) राजन की स्थिति ज्ञात कीजिए।
Find the position of Rajan.
Answer : B(6, 7)
(ii) प्रवीण की स्थिति ज्ञात कीजिए।
Find the position of Praveen.
Answer : C(9, 4)
(iii) AC के मध्यबिन्दु के निर्देशांक ज्ञात कीजिए।
Find the coordinates of the mid point of AC.
Answer : (6, 4)
(iv) प्रवीण की मूल बिन्दु से दूरी ज्ञात कीजिए।
Find the distance of Praveen from origin.
Answer : Here C(9, 4) and O(0, 0)
x1 = 9, x2 = 0, y1 = 4, y2 = 0
Using Distance Formula,
CO = √(x2–x1)2+(y2–y1)2
= √(0–9)2+(0–4)2
= √(–9)2+(–4)2
= √16+81
= √97 units
