Haryana Board (HBSE) Class 10 Maths Question Paper 2025 with a fully solved answer key. Students can use this HBSE Class 10 Mathematics Solved Paper to match their responses and understand the question pattern. This BSEH Math Answer Key 2025 is based on the latest syllabus and exam format to support accurate preparation and revision for the board exams.
HBSE Class 10 Maths (Basic) Question Paper 2025 Answer Key
SECTION – A (1 Mark)
1. संख्या 7 × 11 × 13 × 15 + 15 है, एक :
(A) अभाज्य संख्या
(B) भाज्य संख्या
(C) न भाज्य न अभाज्य
(D) इनमें से कोई नहीं
उत्तर : (B) भाज्य संख्या
7 × 11 × 13 × 15 + 15
= 15(7 × 11 × 13 + 1)
= 15(1001 + 1)
= 15 × 1002
Number 7 × 11 × 13 × 15 + 15 is a :
(A) Prime number
(B) Composite number
(C) Neither prime nor composite
(D) None of these
Answer : (B) Composite number
7 × 11 × 13 × 15 + 15
= 15(7 × 11 × 13 + 1)
= 15(1001 + 1)
= 15 × 1002
2. यदि HCF (a, 8) = 4 तथा LCM (a, 8) = 24 तब a है :
(A) 6
(B) 8
(C) 10
(D) 12
उत्तर : (D) 12
संख्याओं का गुणनफल = HCF × LCM
a × 8 = HCF × LCM
a × 8 = 4 × 24
a = 96 ÷ 8 = 12
If HCF (a, 8) = 4 and LCM (a, 8) = 24 then a is :
(A) 6
(B) 8
(C) 10
(D) 12
Answer : (D) 12
Product of numbers = HCF × LCM
a × 8 = HCF × LCM
a × 8 = 4 × 24
a = 96 ÷ 8 = 12
3. संख्या (√3 + √5)2 है, एक :
(A) अवास्तविक संख्या
(B) परिमेय संख्या
(C) अपरिमेय संख्या
(D) पूर्णांक
उत्तर : (C) अपरिमेय संख्या
(√3 + √5)2 = 3 + 5 + 2√15 = 8 + 2√15
The number (√3 + √5)2 is a :
(A) Not a real number
(B) Rational number
(C) Irrational number
(D) Integer
Answer : (C) Irrational number
(√3 + √5)2 = 3 + 5 + 2√15 = 8 + 2√15
4. शून्यक –7 और 3 वाले बहुपद की घात है :
(A) 0
(B) 1
(C) 2
(D) 3
उत्तर : (C) 2
The degree of polynomial having zeroes –7 and 3 is :
(A) 0
(B) 1
(C) 2
(D) 3
Answer : (C) 2
5. द्विघात समीकरण x2 + 2x – 143 = 0 का विविक्तकर होगा :
(A) 576
(B) 625
(C) 676
(D) 729
उत्तर : (A) 576
यहाँ a = 1, b = 2, c = –143
विविक्तकर (D) = b2 – 4ac
= (2)2 – 4(1)(–143)
= 4 + 572
= 576
The discriminant of quadratic equation x2 + 2x – 143 = 0 is :
(A) 576
(B) 625
(C) 676
(D) 729
Answer : (A) 576
Here a = 1, b = 2, c = –143
Discriminant (D) = b2 – 4ac
= (2)2 – 4(1)(–143)
= 4 + 572
= 576
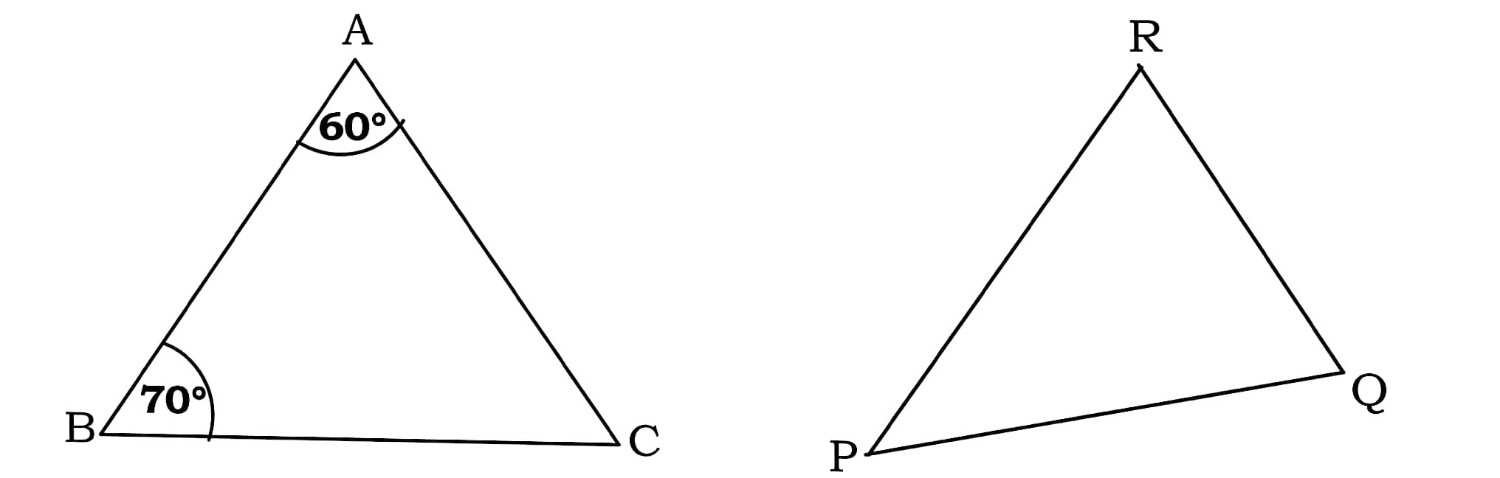
6. आकृति में ∆ABC ~ ∆QPR , तो ∠R + ∠P है :
(A) 110°
(B) 120°
(C) 130°
(D) इनमें से कोई नहीं
उत्तर : (B) 120°
∠A = 60°, ∠B = 70°
∠C = 180° – (70° + 60°) = 50°
∠R + ∠P = ∠C + ∠B = 50° + 70° = 120°
In figure, ∆ABC ~ ∆QPR, then angle ∠R + ∠P :

(A) 110°
(B) 120°
(C) 130°
(D) None of these
Answer : (B) 120°
∠A = 60°, ∠B = 70°
∠C = 180° – (70° + 60°) = 50°
∠R + ∠P = ∠C + ∠B = 50° + 70° = 120°
7. बिन्दुओं (–8/5, –2) तथा (7/5, 3) के बीच की दूरी है ………….
उत्तर : यहाँ x1 = –8/5, y1 = –2, x2 = 7/5, y2 = 3
दूरी = √(x2–x1)2+(y2–y1)2
= √(7/5+8/5)2+(3+2)2
= √32+52
= √9+25
= √34 इकाई
The distance between the points (–8/5, –2) and (7/5, 3) is ………….
Answer : Here x1 = –8/5, y1 = –2, x2 = 7/5, y2 = 3
Distance = √(x2–x1)2+(y2–y1)2
= √(7/5+8/5)2+(3+2)2
= √32+52
= √9+25
= √34 unit
8. सत्य या असत्य बताइए, यदि secθ = 4/3, θ के किसी मान के लिए।
उत्तर : सत्य
secθ = 4/3 → cosθ = 3/4
क्योंकि cosθ का मान 0 और 1 के बीच हो सकता है, इसलिए ऐसा θ संभव है।
State true or false, whether secθ = 4/3 for some angle θ.
Answer : True
secθ = 4/3 → cosθ = 3/4
Since the value of cosθ lies between 0 and 1, such an angle θ is possible.
9. 2√2 cos45°.cos60° + 2√3 sin30°.tan60° – cos0° का मान है :
(A) 3
(B) √3/2
(C) 1/2
(D) 1
उत्तर : (A) 3
2√2 × (1/√2) × (1/2) + 2√3 × (1/2) × √3 – 1
= 1 + 3 – 1
= 3
The value of 2√2 cos45°.cos60° + 2√3 sin30°.tan60° – cos0° is :
(A) 3
(B) √3/2
(C) 1/2
(D) 1
Answer : (A) 3
2√2 × (1/√2) × (1/2) + 2√3 × (1/2) × √3 – 1
= 1 + 3 – 1
= 3
10. खाली स्थान भरें :
7cot2A – 7cosec2A = …………
उत्तर : –7(cosec2A – cot2A) = –7(1) = –7
Fill in the blanks :
7cot2A – 7cosec2A = …………
Answer : –7(cosec2A – cot2A) = –7(1) = –7
11. एक 6 मी० ऊँचा खम्भा सूर्य के 60° उन्नयन कोण के साथ भूमि पर छाया बनाता है। उस छाया की लंबाई है :
(A) √3 m
(B) 2√3 m
(C) 3√3 m
(D) 6 m
उत्तर : (B) 2√3 m
खम्भे की ऊँचाई = 6 मी०, उन्नयन कोण = 60°
tanθ = P/B
tan60° = ऊँचाई / छाया
√3 = 6 / छाया
छाया = 6/√3 = 2√3 m
A pole 6 m high casts a shadow on ground with Sun’s elevation 60°. The length of shadow is :
(A) √3 m
(B) 2√3 m
(C) 3√3 m
(D) 6 m
Answer : (B) 2√3 m
Height of pole = 6 m, Angle of elevation = 60°
tanθ = Perpendicular / Base
tan60° = Height / Shadow
√3 = 6 / Shadow
Shadow = 6/√3 = 2√3 m
12. यदि एक बिन्दु P से O केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 70° के कोण पर झुकी हो, तो ∠POA बराबर है :
(A) 45°
(B) 50°
(C) 55°
(D) 60°
उत्तर : (C) 55°
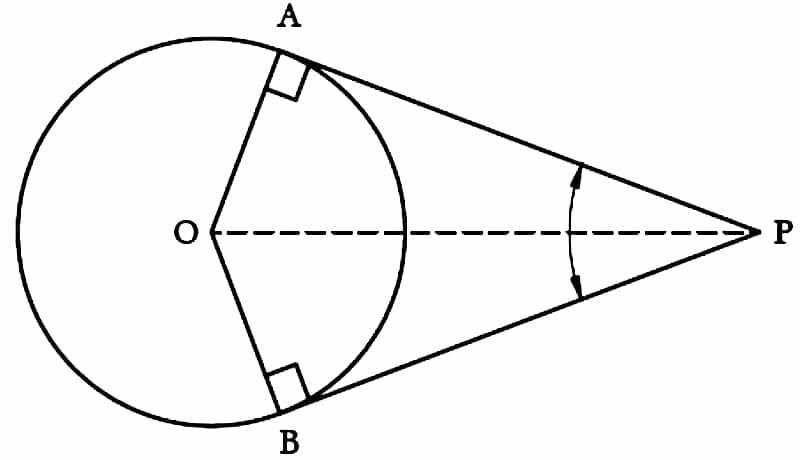
∠APB = 70°, ∠APO = 70°/2 = 35°
∠POA + ∠PAO + ∠APO = 180°
∠POA + 90° + 35° = 180°
∠POA = 180° − (90° + 35°) = 180° – 125° = 55°
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 70°, then ∠POA is equal to :
(A) 45°
(B) 50°
(C) 55°
(D) 60°
Answer : (C) 55°

∠APB = 70°, ∠APO = 70°/2 = 35°
∠POA + ∠PAO + ∠APO = 180°
∠POA + 90° + 35° = 180°
∠POA = 180° − (90° + 35°) = 180° – 125° = 55°
13. वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को ………….. कहते हैं।
उत्तर : स्पर्श बिन्दु
The common point of a tangent to a circle and the circle is called ………….
Answer : Point of contact
14. 28 cm व्यास वाले वृत्त के एक त्रिज्यखंड का क्षेत्रफल क्या होगा, जिसका कोण 72° है।
उत्तर : व्यास = 28 सेमी, त्रिज्या (r) = 28/2 = 14 सेमी
त्रिज्यखंड का क्षेत्रफल = θ/360° × πr2
= = 72°/360° × 22/7 × (14)2
= 123.2 cm2
Find the area of a sector of a circle with diameter 28 cm, if angle of the sector is 72°.
Answer : Diameter = 28 cm, Radius (r) = 28/2 = 14 cm
Area of sector = θ/360° × πr2
= 72°/360° × 22/7 × (14)2
= 123.2 cm2
15. व्यास r वाले वृत्त के कोण θ वाले चाप की लम्बाई है :
(A) θ/360° × πr2
(B) θ/360° × 2πr
(C) θ/360° × πr
(D) θ/360° × 2πr2
उत्तर : (C) θ/360° × πr
यहाँ वृत्त का व्यास = r
त्रिज्या = व्यास/2 = r/2
चाप की लम्बाई = θ/360° × 2π(त्रिज्या)
= θ/360° × 2π(r/2)
= θ/360° × πr
The length of an arc of angle θ of a circle with diameter r is :
(A) θ/360° × πr2
(B) θ/360° × 2πr
(C) θ/360° × πr
(D) θ/360° × 2πr2
Answer : (C) θ/360° × πr
Here Diameter = r
Radius = Diameter/2 = r/2
Length of arc = θ/360° × 2π(radius)
= θ/360° × 2π(r/2)
= θ/360° × πr
16. यदि एक गोले का आयतन 12π cm3 है, तो गोले की त्रिज्या होगी :
(A) 31/3 cm
(B) 32/3 cm
(C) 3√3 cm
(D) 3 cm
उत्तर : (B) 32/3 cm
गोले का आयतन = 4/3 πr3 = 12π
r3 = 9
r = 91/3 = (32)1/3 = 32/3
The radius of a sphere whose volume is 12π cm3 will be :
(A) 31/3 cm
(B) 32/3 cm
(C) 3√3 cm
(D) 3 cm
Answer : (B) 32/3 cm
गोले का आयतन = 4/3 πr3 = 12π
r3 = 9
r = 91/3 = (32)1/3 = 32/3
17. यदि P(A) घटना A की प्रायिकता व्यक्त करता है, तो :
(A) P(A) < 0
(B) P(A) > 1
(C) –1 ≤ P(A) ≤ 1
(D) 0 ≤ P(A) ≤ 1
उत्तर : (D) 0 ≤ P(A) ≤ 1
If P(A) denotes the probability of an event A, then :
(A) P(A) < 0
(B) P(A) > 1
(C) –1 ≤ P(A) ≤ 1
(D) 0 ≤ P(A) ≤ 1
Answer : (D) 0 ≤ P(A) ≤ 1
18. निम्नलिखित बारंबारता बंटन में बहुलक वर्ग की उच्च वर्ग सीमा है :
| वर्ग अन्तराल | 0-5 | 6-11 | 12-17 | 18-23 | 24-29 |
| बारंबारता | 13 | 10 | 15 | 8 | 11 |
(A) 16.5
(B) 17
(C) 17.5
(D) 18
उत्तर : (C) 17.5
सबसे अधिक बारंबारता 15 है, जो वर्ग 12-17 से संबंधित है।
अतः बहुलक वर्ग (Modal Class) = 12-17
अब इसे continuous बनाने पर:
12-17 → 11.5-17.5
इसलिए बहुलक वर्ग की उच्च वर्ग सीमा = 17.5
The upper limit of the modal class of following frequency distribution is :
| Class Interval | 0-5 | 6-11 | 12-17 | 18-23 | 24-29 |
| Frequency | 13 | 10 | 15 | 8 | 11 |
(A) 16.5
(B) 17
(C) 17.5
(D) 18
Answer : (C) 17.5
The highest frequency is 15, which corresponds to the class interval 12-17.
Therefore, the modal class is 12-17
After converting it into a continuous class:
12-17 → 11.5-17.5
Hence, the upper class boundary of the modal class is 17.5
19. अभिकथन (A) : यदि एक A.P. का nवाँ पद (2n+1) है, तो उसके पहले तीन पदों का योग 15 है।
तर्क (R) : पहली n प्राकृतिक संख्याओं का योग n(n+1)/2 है।
विकल्प :
(A) अभिकथन (A) और तर्क (R) दोनों सही हैं और तर्क (R) अभिकथन (A) की सही व्याख्या करता है।
(B) अभिकथन (A) और तर्क (R) दोनों सही हैं, लेकिन तर्क (R) अभिकथन (A) की सही व्याख्या नहीं करता है।
(C) अभिकथन (A) सही है, लेकिन तर्क (R) गलत है।
(D) अभिकथन (A) गलत है, लेकिन तर्क (R) सही है।
उत्तर : (B) अभिकथन (A) और तर्क (R) दोनों सही हैं, लेकिन तर्क (R) अभिकथन (A) की सही व्याख्या नहीं करता है।
(क्योंकि यहाँ A.P. के पदों का योग निकाला गया है, न कि प्राकृतिक संख्याओं का)
यदि A.P. का nवाँ पद (2n+1) है, तो पहले तीन पद होंगे,
a1 = 3, a2 = 5, a3 = 7
जोड़ = 3 + 5 + 7 = 15
पहली n प्राकृतिक संख्याओं का योग n(n+1)/2 होता है, जिसका इस स्थिति में उपयोग नहीं किया गया है।
Assertion (A) : If nth term of an A.P. is (2n+1), then the sum of its first three terms is 15.
Reason (R) : The sum of first n natural numbers is n(n+1)/2.
Option :
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not correct explanation of Assertion (A).
(C) Assertion (A) is true, but Reason (R) is false.
(D) Assertion (A) is false, but Reason (R) is true.
Answer : (B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not correct explanation of Assertion (A).
(Because here we are finding the sum of the terms of an A.P., not the sum of natural numbers)
If the nth term of an A.P. is (2n+1), then the first three terms are :
a1 = 3, a2 = 5, a3 = 7
Sum = 3 + 5 + 7 = 15
The sum of the first n natural numbers is n(n+1)/2, which is not used in this case.
20. अभिकथन (A) : किसी वृत्त के एक व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।
तर्क (R) : वृत्त का व्यास उसकी सबसे बड़ी जीवा होती है।
विकल्प :
(A) अभिकथन (A) और तर्क (R) दोनों सही हैं और तर्क (R) अभिकथन (A) की सही व्याख्या करता है।
(B) अभिकथन (A) और तर्क (R) दोनों सही हैं, लेकिन तर्क (R) अभिकथन (A) की सही व्याख्या नहीं करता है।
(C) अभिकथन (A) सही है, लेकिन तर्क (R) गलत है।
(D) अभिकथन (A) गलत है, लेकिन तर्क (R) सही है।
उत्तर : (B) अभिकथन (A) और तर्क (R) दोनों सही हैं, लेकिन तर्क (R) अभिकथन (A) की सही व्याख्या नहीं करता है।
Assertion (A) : The tangents drawn at the end points of a diameter of a circle are parallel.
Reason (R) : Diameter of a circle is its longest chord.
Option :
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not correct explanation of Assertion (A).
(C) Assertion (A) is true, but Reason (R) is false.
(D) Assertion (A) is false, but Reason (R) is true.
Answer : (B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not correct explanation of Assertion (A).
SECTION – B (2 Marks)
21. निम्नलिखित रैखिक समीकरणों के युग्म को हल करें :
0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
उत्तर :
दोनों समीकरणों को 10 से गुणा करने पर,
2x + 3y = 13 …..(i)
4x + 5y = 23 …..(ii)
समीकरण (i) को 2 से गुणा करने पर,
4x + 6y = 26 …..(iii)
अब समीकरण (ii) को (iii) से घटाने पर,
(4x + 6y) – (4x + 5y) = 26 – 23
y = 3
अब y = 3 का मान समीकरण (i) में रखने पर,
2x + 3(3) = 13
2x + 9 = 13
2x = 13 – 9
2x = 4
x = 4/2 = 2
अतः x = 2 और y = 3
Solve the following pair of linear equations :
0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
Answer :
Multiply both equations by 10,
2x + 3y = 13 …..(i)
4x + 5y = 23 …..(ii)
Multiply eqn.(i) by 2,
4x + 6y = 26 …..(iii)
Subtract eqn.(ii) from eqn.(iii),
(4x + 6y) – (4x + 5y) = 26 – 23
y = 3
Put y = 3 in eqn.(i),
2x + 3(3) = 13
2x + 9 = 13
2x = 13 – 9
2x = 4
x = 4/2 = 2
Hence x = 2 and y = 3.
OR
निम्नलिखित रैखिक समीकरणों के युग्म को हल करें :
3x/2 – 5y/3 = – 2 और x/3 + y/2 = 13/6
उत्तर :
3x/2 – 5y/3 = – 2 ……..(i)
x/3 + y/2 = 13/6 ……..(ii)
समीकरण (i) और (ii) को 6 से गुणा करने पर,
9x – 10y = – 12 …….(iii)
2x + 3y = 13 …….(iv)
अब समीकरण (iii) को 3 से तथा समीकरण (iv) को 10 से गुणा करने पर,
27x – 30y = – 36 ……..(v)
20x + 30y = 130 …….(vi)
समीकरण (v) और (vi) को जोड़ने पर,
(27x – 30y) + (20x + 30y) = – 36 + 130
47x = 94
x = 94/47 = 2
अब x = 2 का मान समीकरण (iv) में रखने पर,
2(2) + 3y = 13
4 + 3y = 13
3y = 13 – 4
3y = 9
y = 9/3 = 3
अतः x = 2 और y = 3
Solve the following pair of linear equations :
3x/2 – 5y/3 = – 2 and x/3 + y/2 = 13/6
Answer :
3x/2 – 5y/3 = – 2 ……..(i)
x/3 + y/2 = 13/6 ……..(ii)
Multiply eqn.(i) & (ii) by 6,
9x – 10y = – 12 …….(iii)
2x + 3y = 13 …….(iv)
Multiply eqn.(iii) by 3 & eqn.(iv) by 10,
27x – 30y = – 36 ……..(v)
20x + 30y = 130 …….(vi)
Add eqn.(v) & (vi),
(27x – 30y) + (20x + 30y) = – 36 + 130
47x = 94
x = 94/47 = 2
Put x = 2 in eqn.(iv),
2(2) + 3y = 13
4 + 3y = 13
3y = 13 – 4
3y = 9
y = 9/3 = 3
Hence x = 2 and y = 3.
22. यदि कोई रेखा एक ∆ABC की भुजाओं AB और AC को क्रमशः D और E पर प्रतिच्छेद करे तथा भुजा BC के समांतर हो, तो सिद्ध कीजिए कि AD/AB = AE/AC होगा।
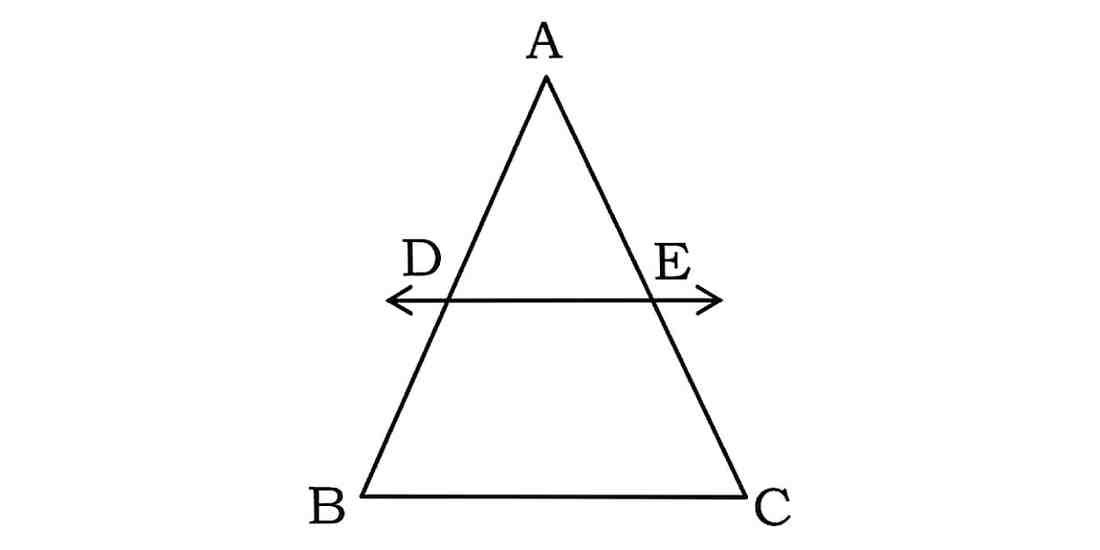
उत्तर :
दिया है: त्रिभुज ∆ABC में, रेखा DE भुजाओं AB और AC को क्रमशः बिन्दुओं D और E पर प्रतिच्छेद करती है तथा DE || BC है।
सिद्ध करना है: AD/AB = AE/AC
प्रमाण: त्रिभुज ∆ADE और ∆ABC पर विचार करें,
चूँकि DE || BC, इसलिए
∠ADE = ∠ABC (संगत कोण)
∠AED = ∠ACB (संगत कोण)
अतः,
∆ADE ~ ∆ABC (AA समानता के आधार पर)
इसलिए, समान त्रिभुजों की संगत भुजाएँ समान अनुपात में होती हैं,
AD/AB = AE/AC
अतः सिद्ध हुआ।
If a line intersects sides AB and AC of a ∆ABC at points D and E respectively and is parallel to BC, prove that AD/AB = AE/AC.

Answer :
Given: In ∆ABC, a line DE intersects AB and AC at points D and E respectively and DE || BC
To prove: AD/AB = AE/AC
Proof: Consider triangles ∆ADE and ∆ABC.
Since DE || BC,
∠ADE = ∠ABC (corresponding angles)
∠AED = ∠ACB (corresponding angles)
Therefore,
∆ADE ~ ∆ABC (by AA similarity)
Hence, corresponding sides of similar triangles are proportional,
AD/AB = AE/AC
Hence Proved.
23. m का वह मान ज्ञात कीजिए जिसके लिए बिन्दुओं A(–3, –14) तथा B(m, –5) की दूरी 9 इकाई है।
उत्तर : यहाँ x1 = –3, y1 = –14, x2 = m, y2 = –5
दूरी = √(x2–x1)2+(y2–y1)2 = 9
(m + 3)2 + (–5 + 14)2 = 92
(m + 3)2 + (9)2 = 81
(m + 3)2 + 81 = 81
(m + 3)2 = 81 – 81
(m + 3)2 = 0
m + 3 = 0
m = – 3
Find the value of m, if the distance between the points A(–3, –14) तथा B(m, –5) is 9 units.
Answer : Here x1 = –3, y1 = –14, x2 = m, y2 = –5
Distance = √(x2–x1)2+(y2–y1)2 = 9
(m + 3)2 + (–5 + 14)2 = 9²
(m + 3)2 + (9)2 = 81
(m + 3)2 + 81 = 81
(m + 3)2 = 81 – 81
(m + 3)2 = 0
m + 3 = 0
m = – 3
24. यदि cotθ = 7/8, तो (1+cosθ)(1–cosθ) / (1–sinθ)(1+sinθ) का मान ज्ञात कीजिए।
उत्तर : cotθ = 7/8 → tanθ = 8/7
= (1+cosθ)(1–cosθ) / (1–sinθ)(1+sinθ)
= (12 – cos2θ) / (12 – sin2θ)
= sin2θ / cos2θ
= tan2θ
= (8/7)2
= 64/49
If cotθ = 7/8, then evaluate (1+cosθ)(1–cosθ) / (1–sinθ)(1+sinθ)
Answer : cotθ = 7/8 → tanθ = 8/7
= (1+cosθ)(1–cosθ) / (1–sinθ)(1+sinθ)
= (12 – cos2θ) / (12 – sin2θ)
= sin2θ / cos2θ
= tan2θ
= (8/7)2
= 64/49
OR
सिद्ध कीजिए :
secθ(1 – sinθ)(secθ + tanθ) = 1
उत्तर : LHS = secθ(1 – sinθ)(secθ + tanθ)
= secθ(1 – sinθ)(1/cosθ + sinθ/cosθ)
= secθ(1 – sinθ) [(1+sinθ)/cosθ)]
= secθ(12 – sin2θ) / cosθ
= (12 – sin2θ) secθ/cosθ
= cos2θ / cos2θ
= 1 = RHS
अतः सिद्ध हुआ
Prove that :
secθ(1 – sinθ)(secθ + tanθ) = 1
Answer : LHS = secθ(1 – sinθ)(secθ + tanθ)
= secθ(1 – sinθ)(1/cosθ + sinθ/cosθ)
= secθ(1 – sinθ) [(1+sinθ)/cosθ)]
= secθ(12 – sin2θ) / cosθ
= (12 – sin2θ) secθ/cosθ
= cos2θ / cos2θ
= 1 = RHS
Hence Proved.
25. एक वृत्ताकार ब्रूच (brooch) को चाँदी के तार से बनाया जाना है जिसका व्यास 42 mm है। तार को वृत्त के तीन व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 6 बराबर त्रिज्यखंडों में विभाजित करता है। कुल वांछित चाँदी की तार की लंबाई ज्ञात कीजिए।
उत्तर : वृत्ताकार ब्रोच का व्यास = 42 mm
त्रिज्या (r) = d/2 = 42/2 = 21 mm
तार का उपयोग एक वृत्ताकार छल्ला तथा वृत्त के 3 व्यास बनाने में किया गया है।
वृत्ताकार तार की लंबाई = वृत्त की परिधि = 2πr = 2 × 22/7 × 21 = 132 mm
3 व्यासों की लंबाई = 3 × 42 = 126 mm
अतः चाँदी की तार की कुल लंबाई = 132 + 126 = 258 mm
A brooch is made with silver wire in the form of a circle with diameter 42 mm. The wire is also used in making 3 diameters which divide the circle into 6 equal sectors. Find the total length of silver wire.
Answer : Diameter of the circular brooch = 42 mm
Radius (r) = d/2 = 42/2 = 21 mm
The wire is used to make one circular ring and 3 diameters of the circle.
Length of circular wire = circumference of circle = 2πr = 2 × 22/7 × 21 = 132 mm
Length of 3 diameters = 3 × 42 = 126 mm
Total length of silver wire = 132 + 126 = 258 mm
SECTION – C (3 Marks)
26. सिद्ध कीजिए 2 – 3√5 एक अपरिमेय संख्या है, यदि √5 एक अपरिमेय संख्या है।
उत्तर : मान लीजिए कि 2 – 3√5 एक परिमेय संख्या है।
तब, हम ऐसे पूर्णांक p और q (q ≠ 0) ज्ञात कर सकते हैं कि
2 – 3√5 = p/q
उपरोक्त समीकरण को पुनर्व्यवस्थित करने पर, हमें प्राप्त होता है,
3√5 = 2 – p/q
3√5 = (2q – p)/3q
दोनों पक्षों को 3 से भाग देने पर, हमें प्राप्त होता है,
√5 = (2q – p)/q
यहाँ (2q – p)/3q एक परिमेय संख्या है, क्योंकि यह दो पूर्णांकों का अनुपात है।
लेकिन √5 एक अपरिमेय संख्या है। यह एक विरोधाभास है।
यह विरोधाभास हमारी इस गलत धारणा के कारण उत्पन्न हुआ है कि 2 – 3√5 एक परिमेय संख्या है। अतः 2 – 3√5 एक अपरिमेय संख्या है।
Prove that 2 – 3√5 is an irrational number, if √5 is an irrational number.
Answer : Let us assume, to the contrary, that 2 – 3√5 is a rational number.
Then, we can find integers p and q (q ≠ 0) such that
2 – 3√5 = p/q
Rearranging the above equation, we get
3√5 = 2 – p/q
3√5 = (2q–p)/3q
Dividing both sides by 3, we obtain
√5 = (2q–p)/q
Here, (2q–p)/3q is a rational number, since it is the ratio of two integers.
But √5 is given to be an irrational number. This is a contradiction.
This contradiction has arisen due to our incorrect assumption that 2 – 3√5 is a rational number.
Hence, 2 – 3√5 is an irrational number.
27. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों के योग तथा गुणनफल क्रमशः √2 तथा 1/2 हैं।
उत्तर : यहाँ α + β = √2, αβ = 1/2
शून्यकों (α, β) के पदों में द्विघात बहुपद निम्न प्रकार से दिया जाता है:
= x2 − (शून्यकों का योग)x + शून्यकों का गुणनफल
= x2 − (α + β)x + αβ
= x2 − √2x + 1/2
= 2x2 – 2√2x + 1
Find a quadratic polynomial, where sum and product of its zeroes are respectively √2 and 1/2.
Answer : Here α + β = √2, αβ = 1/2
A quadratic polynomial in terms of the zeroes (α, β) is given by:
= x2 − (sum of zeroes)x + product of zeroes
= x2 − (α + β)x + αβ
= x2 − √2x + 1/2
= 2x2 – 2√2x + 1
28. k का वह मान ज्ञात कीजिए जिसके लिए इन रैखिक समीकरणों के युग्म के अपरिमित अनेक हल होंगे :
kx + 3y – (k – 3) = 0
12x + ky – k = 0
उत्तर : तुलना करें ax + by + c = 0 से
यहाँ a1 = k, b1 = 3, c1 = –(k – 3)
a2 = 12, b2 = k, c2 = –k
अनंत हल होने पर,
a1/a2 = b1/b2 = c1/c2
k/12 = 3/k = –(k–3)/(–k)
पहले दो अनुपातों से,
k/12 = 3/k
k2 = 36
k = √36 = ±6
साथ ही, अंतिम दो अनुपातों से,
3/k = –(k–3)/(–k)
3k = k(k – 3)
3k = k2 – 3k
k2 = 6k
k = 6
k का वह मान जो दोनों समीकरणों को संतुष्ट करता है, 6 है।
इस प्रकार, k = 6 के लिए, रैखिक समीकरणों के युग्म के अनंत हल होते हैं।
Find the value(s) of k for which the pair of linear equations will have infinitely many solutions:
kx + 3y – (k – 3) = 0
12x + ky – k = 0
Answer : Compare with ax + by + c = 0
Here a1 = k, b1 = 3, c1 = –(k – 3)
a2 = 12, b2 = k, c2 = –k
For infinitely many solutions,
a1/a2 = b1/b2 = c1/c2
k/12 = 3/k = –(k–3)/(–k)
From the first two ratios,
k/12 = 3/k
k2 = 36
k = √36 = ±6
Also, from the last two ratios,
3/k = –(k–3)/(–k)
3k = k(k – 3)
3k = k2 – 3k
k2 = 6k
k = 6
The value of k which satisfies both the equations is 6.
Thus, for k = 6, the pair of linear equations have infinitely many solutions
OR
एक भिन्न 1/3 हो जाती है, जब उसके अंश से 1 घटाया जाता है और वह 1/4 हो जाती है जब हर में 8 जोड़ दिया जाता है। वह भिन्न ज्ञात कीजिए।
उत्तर : मान लीजिए भिन्न x/y है।
प्रथम शर्त के अनुसार,
(x–1)/y = 1/3
3(x – 1) = y
3x – 3 = y
3x – y = 3 ……..(i)
द्वितीय शर्त के अनुसार,
x/(y+8) = 1/4
4x = y + 8
4x – y = 8 …….(ii)
समीकरण (ii) से समीकरण (i) घटाने पर,
(4x – y) – (3x – y) = 8 – 3
x = 5
समीकरण (i) में x = 5 रखने पर,
3(5) – y = 3
15 – y = 3
– y = 3 – 15
– y = – 12
y = 12
अतः, भिन्न x/y = 5/12 होगी।
A fraction becomes 1/3, when 1 is subtracted from the numerator and it becomes 1/4, when 8 is added to its denominator. Find the fraction.
Answer : Let the fraction be x/y
According to first condition,
(x–1)/y = 1/3
3(x – 1) = y
3x – 3 = y
3x – y = 3 ……..(i)
According to second condition,
x/(y+8) = 1/4
4x = y + 8
4x – y = 8 …….(ii)
Subtract eqn.(i) from eqn.(ii),
(4x – y) – (3x – y) = 8 – 3
x = 5
Put x = 5 in eqn.(i),
3(5) – y = 3
15 – y = 3
– y = 3 – 15
– y = – 12
y = 12
Thus, the fraction be x/y = 5/12
29. बिन्दुओं (2, –1) और (–3, –2) को जोड़ने वाले रेखाखण्ड को समत्रिभाजित करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
उत्तर : समत्रिभाजित बिंदु एक रेखाखंड को तीन बराबर भागों में विभाजित करते हैं। रेखाखंड AB के लिए, जिसके बिंदु A(2, –1) और B(–3, –2) हैं, दो बिंदु P और Q इस प्रकार मौजूद हैं कि AP = PQ = QB
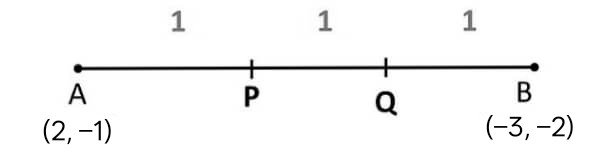
बिंदु P, AB को 1 : 2 के अनुपात में विभाजित करता है।
बिंदु Q, AB को 2 : 1 के अनुपात में विभाजित करता है।
विभाजन सूत्र का प्रयोग करते हुए,
x = (m1x2 + m2x1) ÷ (m1 + m2)
y = (m1y2 + m2y1) ÷ (m1 + m2)
P के लिए, अनुपात 1 : 2 के साथ,
x = [1(–3) + 2(2)] ÷ (1 + 2) = (– 3 + 4) ÷ 3 = 1 ÷ 3 = 1/3
y = [1(–2) + 2(–1)] ÷ (1 + 2) = (– 2 – 2) ÷ 3 = –4 ÷ 3 = – 4/3
इस प्रकार, P = (1/3, –4/3)
Q के लिए, अनुपात 2 : 1 के साथ,
x = [2(–3) + 1(2)] ÷ (2 + 1) = (– 6 + 2) ÷ 3 = – 4 ÷ 3 = – 4/3
y = [2(–2) + 1(–1)] ÷ (1 + 2) = (– 4 – 1) ÷ 3 = – 5 ÷ 3 = – 5/3
इस प्रकार, Q = (–4/3, –5/3)
समत्रिभाजित बिंदुओं के निर्देशांक (1/3, –4/3) और (–4/3, –5/3) हैं।
Find the coordinates of the points of trisection of the line segment joining (2, –1) and (–3, –2).
Answer : Trisection points divide a line segment into three equal parts. For a segment AB with points A(2, –1) and B(–3, –2), two points P and Q exist such that AP = PQ = QB.

Point P divides AB in the ratio 1 : 2
Point Q divides AB in the ratio 2 : 1
Using section formula,
x = (m1x2 + m2x1) ÷ (m1 + m2)
y = (m1y2 + m2y1) ÷ (m1 + m2)
For P with ratio 1 : 2,
x = [1(–3) + 2(2)] ÷ (1 + 2) = (– 3 + 4) ÷ 3 = 1 ÷ 3 = 1/3
y = [1(–2) + 2(–1)] ÷ (1 + 2) = (– 2 – 2) ÷ 3 = –4 ÷ 3 = – 4/3
Thus, P = (1/3, –4/3)
For Q with ratio 2 : 1,
x = [2(–3) + 1(2)] ÷ (2 + 1) = (– 6 + 2) ÷ 3 = – 4 ÷ 3 = – 4/3
y = [2(–2) + 1(–1)] ÷ (1 + 2) = (– 4 – 1) ÷ 3 = – 5 ÷ 3 = – 5/3
Thus, Q = (–4/3, –5/3)
The coordinates of the points of trisection are (1/3, –4/3) and (–4/3, –5/3).
30. सर्वसमिका सिद्ध कीजिए :
(cosecθ – cotθ)2 = (1–cosθ) / (1+cosθ)
उत्तर : LHS = (cosecθ – cotθ)2
= (1/sinθ – cosθ/sinθ)2
= (1 – cosθ)2 / (sinθ)2
= (1 – cosθ)2 / (1 – cos2θ)
= (1 – cosθ)(1 – cosθ) / (1 – cosθ)(1 + cosθ)
= (1–cosθ) / (1+cosθ)
= RHS
Prove the identity :
(cosecθ – cotθ)2 = (1–cosθ) / (1+cosθ)
Answer : LHS = (cosecθ – cotθ)2
= (1/sinθ – cosθ/sinθ)2
= (1 – cosθ)2 / (sinθ)2
= (1 – cosθ)2 / (1 – cos2θ)
= (1 – cosθ)(1 – cosθ) / (1 – cosθ)(1 + cosθ)
= (1–cosθ) / (1+cosθ)
= RHS
OR
सिद्ध कीजिए :
√(sec2θ+cosec2θ) = tanθ + cotθ
उत्तर : LHS = √(sec2θ+cosec2θ)
= √(1 + tan2θ + 1 + cot2θ)
= √(tan2θ + 2 + cot2θ)
= √(tanθ + cotθ)2
= tanθ + cotθ
= RHS
Prove that :
√(sec2θ+cosec2θ) = tanθ + cotθ
Answer : LHS = √(sec2θ+cosec2θ)
= √(1 + tan2θ + 1 + cot2θ)
= √(tan2θ + 2 + cot2θ)
= √(tanθ + cotθ)2
= tanθ + cotθ
= RHS
31. एक नदी के पुल के एक बिन्दु से नदी के सम्मुख किनारों के अवनमन कोण क्रमशः 45° और 30° हैं। यदि पुल किनारों से 5 मी० की ऊँचाई पर हो, तो नदी की चौड़ाई ज्ञात कीजिए।
उत्तर :
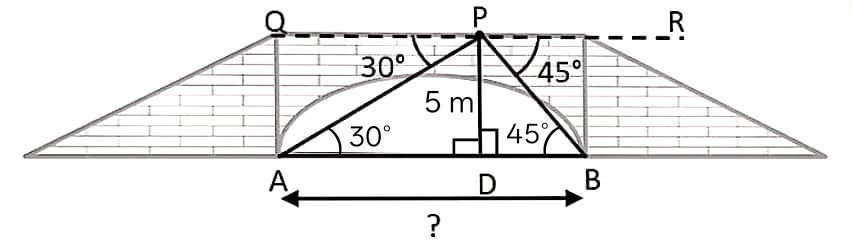
मान लीजिए नदी की चौड़ाई = AB
पुल, नदी के किनारों से 5 मी० की ऊंचाई पर है इसलिए PD = 5 मी०
नदी के विपरीत किनारों के अवनमन कोण क्रमशः 30° और 45° हैं, इसलिए ∠QPA = 30° और ∠RPB = 45°
यहाँ QR || AB है।
∠QPA = ∠PAD = 30°
∠RPB = ∠PBD = 45°
समकोण त्रिभुज ∆PAD में,
tanA = PD/AD
tan30° = 5/AD
1/√3 = 5/AD
AD = 5√3 m
समकोण त्रिभुज ∆PBD में,
tanB = PD/BD
tan45° = 5/BD
1 = 5/BD
BD = 5 m
AB = AD + BD = 5√3 + 5 = 5(√3 + 1) m
नदी की चौड़ाई = 5(√3 + 1) = 5(1.732 + 1) = 5(2.732) m = 13.66 m
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 45° and 30° respectively. If the bridge is at a height of 5 m from the banks, find the width of the river.
Answer :

Let the width of the river = AB
The bridge is at a height of 5 m from the banks, so PD = 5 m
Angles of depression of the banks on opposite sides of the river are 30° and 45° respectively, so ∠QPA = 30° and ∠RPB = 45°
Here QR || AB,
∠QPA = ∠PAD = 30°
∠RPB = ∠PBD = 45°
In right angled triangle ∆PAD,
tanA = PD/AD
tan30° = 5/AD
1/√3 = 5/AD
AD = 5√3 m
In right angled triangle ∆PBD,
tanB = PD/BD
tan45° = 5/BD
1 = 5/BD
BD = 5 m
AB = AD + BD = 5√3 + 5 = 5(√3 + 1) m
Width of the river = 5(√3 + 1) = 5(1.732 + 1) = 5(2.732) m = 13.66 m
SECTION – D (5 Marks)
32. A.P. : 3, 15, 27, 39, ……… का कौन-सा पद उसके 67वें पद से 132 अधिक होगा?
उत्तर : समांतर श्रेणी के nवें पद का सूत्र है, an = a + (n – 1)d
समांतर श्रेणी है: 3, 15, 27, 39, ………
a = 3
d = 15 – 3 = 12
समांतर श्रेणी का 67वाँ पद है,
a54 = a + (67 – 1)d
= 3 + 66 × 12
= 3 + 792
= 795
समांतर श्रेणी के nवें पद को उसके 67वें पद से 132 अधिक मान लीजिए,
हमें प्राप्त होता है: 795 + 132 = 927
an = 927
a + (n – 1)d = 927
3 + (n – 1) × 12 = 927
(n – 1) × 12 = 927 – 3
(n – 1) × 12 = 924
n – 1 = 924/12
n – 1 = 77
n = 77 + 1 = 78
अतः, 78वां पद 67वें पद से 132 अधिक होगा।
Which term of the A.P. : 3, 15, 27, 39, ……… will be 132 more than its 67th term?
Answer : The formula for nth term of an AP is an = a + (n – 1)d
AP is 3, 15, 27, 39, ………
a = 3
d = 15 – 3 = 12
67th term of the AP is,
a54 = a + (67 – 1)d
= 3 + 66 × 12
= 3 + 792
= 795
Let nth term of AP be 132 more than 67th term,
We get: 795 + 132 = 927
an = 927
a + (n – 1)d = 927
3 + (n – 1) × 12 = 927
(n – 1) × 12 = 927 – 3
(n – 1) × 12 = 924
n – 1 = 924/12
n – 1 = 77
n = 77 + 1 = 78
Therefore, the 78th term will be 132 more than the 67th term.
OR
मोबाइल सेट का एक निर्माता तीसरे वर्ष में 700 सेट तथा 7वें वर्ष में 800 सेटों का उत्पादन करता है। यह मानते हुए कि प्रत्येक वर्ष उत्पादन में एकसमान रूप से एक निश्चित संख्या में वृद्धि होती है, ज्ञात कीजिए :
(i) 10वें वर्ष में उत्पादन
(ii) प्रथम 7 वर्षों में कुल उत्पादन
उत्तर :
an = a + (n – 1)d
a3 = a + 2d = 700
a7 = a + 6d = 800
दोनों समीकरणों को हल करें,
(a + 6d) – (a + 2d) = 800 – 700
4d = 100
d = 25
a + 2(25) = 700
a = 700 – 50 = 650
(i) a10 = a + 9d = 650 + 9(25) = 650 + 225 = 875
10वें वर्ष में उत्पादन 875 सेट रहा।
(ii) Sn = n/2 [2a + (n – 1)d]
S7 = 7/2 [2(650) + 6(25)]
= 7/2 [1300 + 150]
= 7/2 (1450)
= 5075
पहले 7 वर्षों में कुल उत्पादन 5075 सेट है।
A manufacturer of Mobile sets produced 700 sets in the third year and 800 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year, find :
(i) the production in the 10th year
(ii) the total production in first 7 years
Answer :
an = a + (n – 1)d
a3 = a + 2d = 700
a7 = a + 6d = 800
Solve both equations,
(a + 6d) – (a + 2d) = 800 – 700
4d = 100
d = 25
a + 2(25) = 700
a = 700 – 50 = 650
(i) a10 = a + 9d = 650 + 9(25) = 650 + 225 = 875
The production in the 10th year is 875 sets.
(ii) Sn = n/2 [2a + (n – 1)d]
S7 = 7/2 [2(650) + 6(25)]
= 7/2 [1300 + 150]
= 7/2 (1450)
= 5075
The total production in the first 7 years is 5075 sets.
33. सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है।
उत्तर :
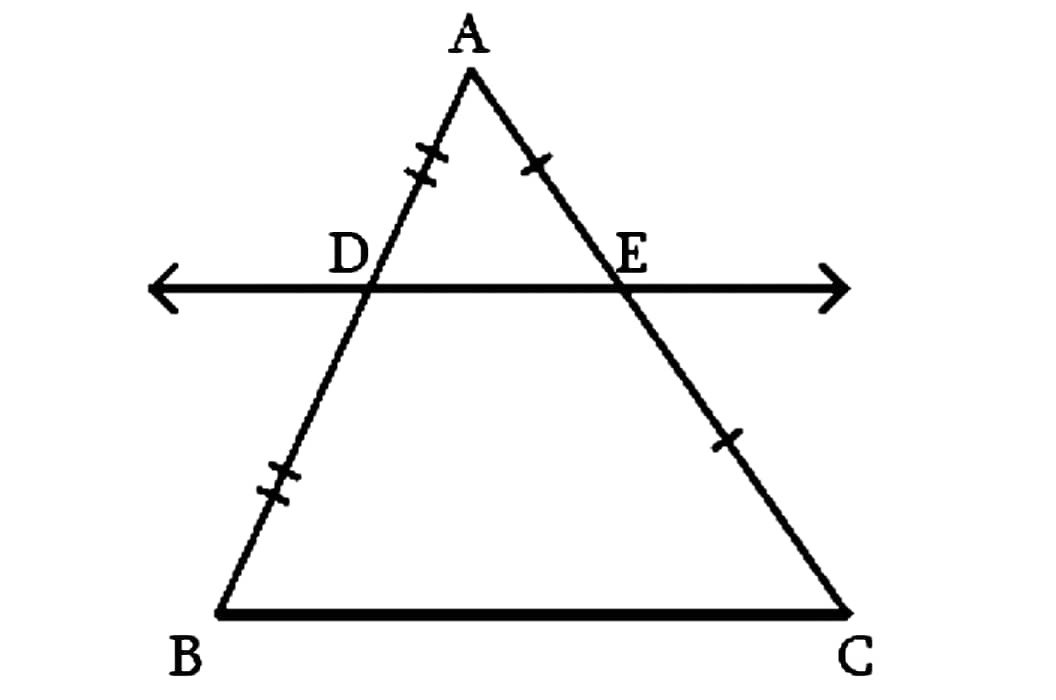
ΔABC में, D, AB का मध्यबिंदु है,
AD = BD
AD/BD = 1 ……….. (i)
E, AC का मध्यबिंदु है,
AE = CE
AE/CE = 1 ………. (ii)
समीकरण (i) और (ii) से,
AD/BD = AE/CE = 1
AD/BD = AE/CE
ΔABC में, मूल समानुपाती प्रमेय के विलोम के अनुसार,
चूंकि, AD/BD = AE/CE
इस प्रकार, DE || BC
अतः सिद्ध हुआ।
Prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Answer :

In ΔABC,
D is the midpoint of AB,
AD = BD
AD/BD = 1 ……….. (i)
E is the midpoint of AC,
AE = CE
AE/CE = 1 ………. (ii)
From equations (i) and (ii),
AD/BD = AE/CE = 1
AD/BD = AE/CE
In ΔABC, according to the Converse of Basic Proportionality theorem,
Since, AD/BD = AE/CE
Thus, DE || BC
Hence, proved.
OR
समान्तर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिन्दु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ~ ∆CFB.
उत्तर :
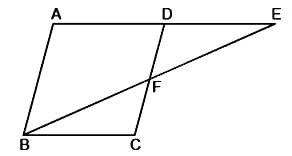
ΔABE और ΔCFB में,
∠BAE = ∠FCB (समांतर चतुर्भुज के विपरीत कोण)
∠AEB = ∠FBC (एकांतर आंतरिक कोण, AE || BC)
अतः, ΔABE ~ ΔCFB (AA समरूपता मानदंड)
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ΑΒΕ ~ ∆CFB.
Answer :

In ΔABE and ΔCFB,
∠BAE = ∠FCB (opposite angles of a parallelogram)
∠AEB = ∠FBC (alternate interior angles, AE || BC)
Thus, ΔABE ~ ΔCFB (AA similarity criterion)
34. कोई बर्तन एक खोखले अर्थगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्थगोले का व्यास 21 cm है और इस बर्तन की कुल ऊँचाई 17 cm है। इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
उत्तर :
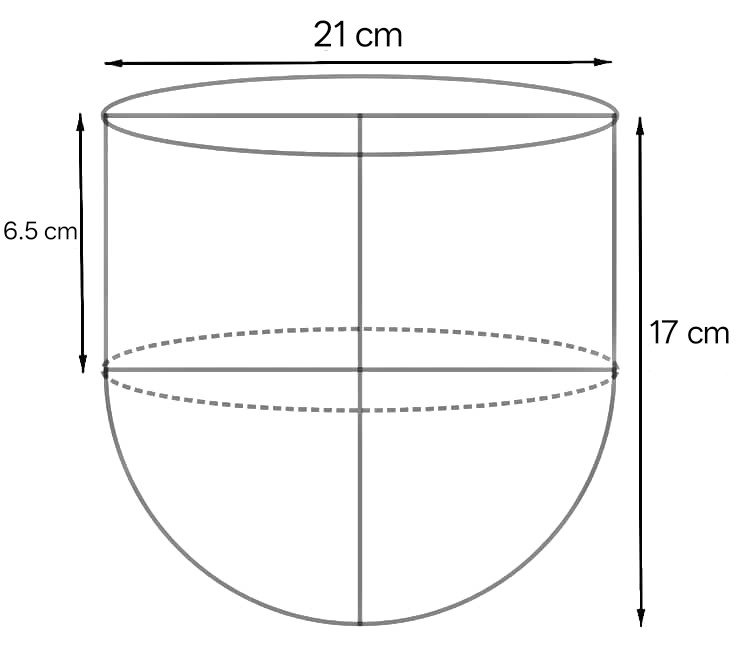
अर्धगोले का व्यास, d = 21 cm
अर्धगोले की त्रिज्या, r = 21/2 = 10.5 cm
अर्धगोले की ऊँचाई = अर्धगोले की त्रिज्या = 10.5 cm
बेलन की त्रिज्या = 10.5 cm
बेलन की ऊँचाई = बर्तन की कुल ऊँचाई – अर्धगोले की ऊँचाई
h = 17 cm – 10.5 cm = 6.5 cm
बर्तन का आंतरिक पृष्ठीय क्षेत्रफल = अर्धगोले का वक्र पृष्ठीय क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल
= 2πr2 + 2πrh
= 2πr(r + h)
= 2 × 22/7 × 10.5 (10.5 + 6.5)
= 2 × 22/7 × 10.5 × 17
= 1122 cm2
अतः, बर्तन का आंतरिक पृष्ठीय क्षेत्रफल 1122 cm2 है।
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 21 cm and the total height of the vessel is 17 cm. Find the inner surface area of the vessel.
Answer :

Diameter of the hemisphere, d = 21 cm
Radius of the hemisphere, r = 21/2 = 10.5 cm
Height of the hemisphere = radius of the hemisphere = 10.5 cm
Radius of the cylinder = 10.5 cm
Height of the cylinder = Total height of the vessel – height of the hemisphere
h = 17 cm – 10.5 cm = 6.5 cm
Inner surface area of the vessel = CSA of the hemisphere + CSA of the cylinder
= 2πr2 + 2πrh
= 2πr(r + h)
= 2 × 22/7 × 10.5 (10.5 + 6.5)
= 2 × 22/7 × 10.5 × 17
= 1122 cm2
Thus, the inner surface area of the vessel is 1122 cm2.
OR
एक जूस बेचने वाला अपने ग्राहकों को आकृति में दर्शाए गिलासों से जूस देता था। बेलनाकार गिलास का आंतरिक व्यास 7 cm था, परन्तु गिलास के निचले आधार (तली) में एक उभरा हुआ अर्धगोला था जिससे गिलास की धारिता कम हो जाती थी। यदि एक गिलास की ऊँचाई 10 cm है, तो गिलास की आभासी धारिता तथा उसकी वास्तविक धारिता ज्ञात कीजिए। (π = 3.14 लीजिए)
उत्तर :
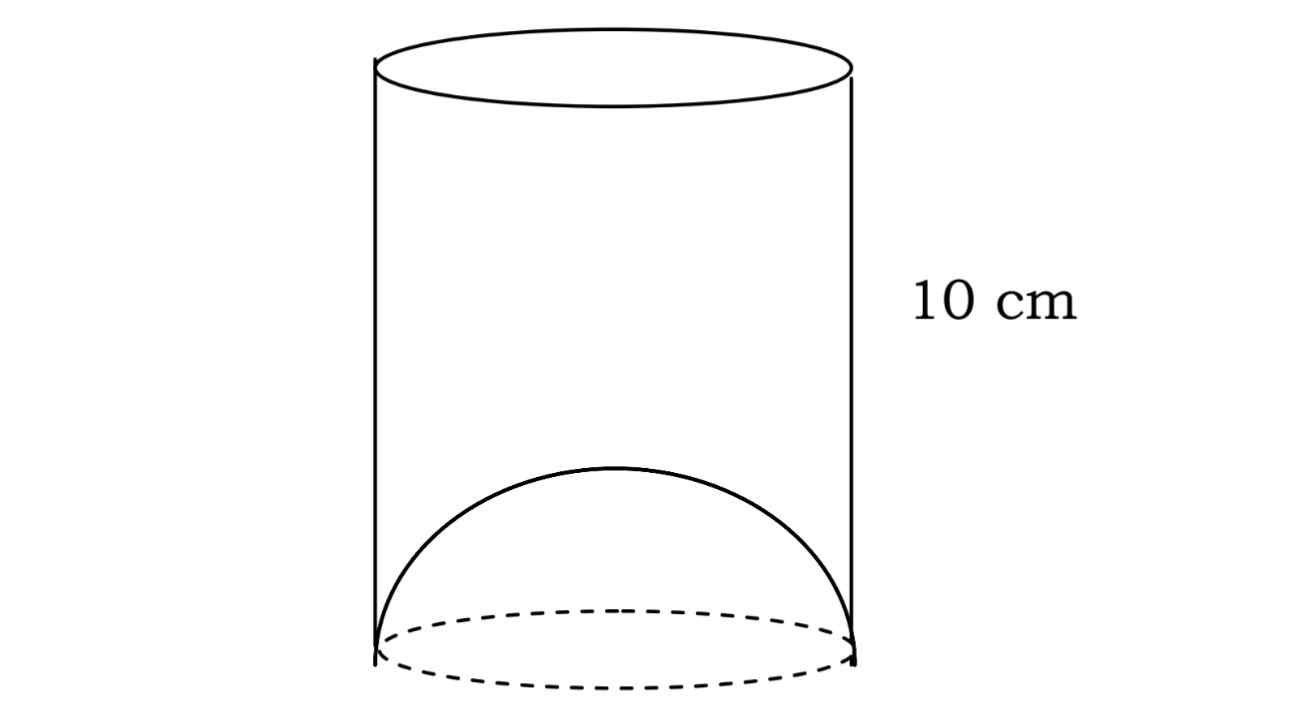
बेलनाकार गिलास का आंतरिक व्यास = 7 cm
त्रिज्या, r = 7/2 = 3.5 cm
गिलास के निचले आधार (तली) में एक उभरा हुआ अर्धगोला की समान त्रिज्या, r = 3.5 cm
आभासी क्षमता = पूर्ण बेलन का आयतन = πr2h
= 3.14 × (3.5)2 × 10
= 384.65 cm3
अर्धगोले का आयतन = 2/3 πr3
= 2/3 × 3.14 × (3.5)3
= 89.75 cm3
वास्तविक क्षमता = आभासी क्षमता – अर्धगोले का आयतन
= 384.65 cm3 – 89.75 cm3
= 294.90 cm3
अतः, गिलास की आभासी क्षमता 384.65 cm3 है और इसकी वास्तविक क्षमता 294.90 cm3 है।
A juice seller was serving his customers using glasses as shown in fig. The inner diameter of the cylindrical glass was 7 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass is 10 cm. Find the apparent capacity of the glass and its actual capacity. (Take π = 3.14)
Answer :

Inner diameter of the cylindrical glass = 7 cm
Radius, r = 7/2 = 3.5 cm
Bottom has a hemispherical raised portion of the same radius, r = 3.5 cm
Apparent capacity = Volume of full cylinder = πr2h = 3.14 × (3.5)2 × 10 = 384.65 cm3
Volume of hemisphere = 2/3 πr3 = 2/3 × 3.14 × (3.5)3 = 89.75 cm3
Actual capacity = Apparent capacity – Volume of hemisphere
= 384.65 cm3 – 89.75 cm3
= 294.90 cm3
Hence, the apparent capacity of the glass is 384.65 cm3 and its actual capacity is 294.90 cm3.
35. दिया गया बंटन विश्व के कुछ श्रेष्ठतम बल्लेबाजों द्वारा एकदिवसीय अंतर्राष्ट्रीय क्रिकेट मैचों में बनाए गए रनों को दर्शाता है :
| बनाए गए रन | बल्लेबाजों की संख्या |
| 3000-4000 | 4 |
| 4000-5000 | 18 |
| 5000-6000 | 9 |
| 6000-7000 | 7 |
| 7000-8000 | 6 |
| 8000-9000 | 3 |
| 9000-10000 | 1 |
| 10000-11000 | 1 |
इन आँकड़ों का बहुलक ज्ञात कीजिए।
उत्तर : बहुलक वर्ग = 4000-5000
वर्ग का आकार, h = 1000
बहुलक वर्ग की निचली सीमा, l = 4000
बहुलक वर्ग की आवृत्ति, f1 = 18
बहुलक वर्ग से पहले वाले वर्ग की आवृत्ति, fo = 4
बहुलक वर्ग के बाद वाले वर्ग की आवृत्ति, f2 = 9
बहुलक = l + [(f1 – fo)/(2f1 – fo – f2)] × h
= 4000 + [(18 – 4)/(2×18 – 4 – 9)] × 1000
= 4000 + [14/(36–13)] × 1000
= 4000 + (14/23) × 1000
= 4000 + 608.695
= 4608.695
= 4608.7
अतः बहुलक 4608.7 है।
The given distribution shows the number of run scored by some top batsmen of the world in one-day international cricket matches :
| Run Scored | No. of Batsmen |
| 3000-4000 | 4 |
| 4000-5000 | 18 |
| 5000-6000 | 9 |
| 6000-7000 | 7 |
| 7000-8000 | 6 |
| 8000-9000 | 3 |
| 9000-10000 | 1 |
| 10000-11000 | 1 |
Find the Mode of the data.
Answer : Modal class = 4000-5000
Class size, h = 1000
Lower limit of modal class, l = 4000
Frequency of modal class, f1 = 18
Frequency of class preceding modal class, fo = 4
Frequency of class succeeding the modal class, f2 = 9
Mode = l + [(f1 – fo)/(2f1 – fo – f2)] × h
= 4000 + [(18 – 4)/(2×18 – 4 – 9)] × 1000
= 4000 + [14/(36–13)] × 1000
= 4000 + (14/23) × 1000
= 4000 + 608.695
= 4608.695
= 4608.7
Hence the mode is 4608.7
OR
नीचे दिया गया बंटन एक कक्षा के 30 विद्यार्थियों के भार को दर्शा रहा है। विद्यार्थियों का माध्यक भार ज्ञात कीजिए :
| भार (कि०ग्रा० में) | विद्यार्थियों की संख्या |
| 40-45 | 2 |
| 45-50 | 3 |
| 50-55 | 8 |
| 55-60 | 6 |
| 60-65 | 6 |
| 65-70 | 3 |
| 70-75 | 2 |
उत्तर :
| भार (कि०ग्रा० में) वर्ग अन्तराल | विद्यार्थियों की संख्या (f) | संचयी बारंबारता (cf) |
| 40-45 | 2 | 2 |
| 45-50 | 3 | 2+3=5 |
| 50-55 | 8 | 5+8=13 |
| 55-60 | 6 | 13+6=19 |
| 60-65 | 6 | 19+6=25 |
| 65-70 | 3 | 25+3=28 |
| 70-75 | 2 | 28+2=30 |
कुल बारंबारता, n = 30 → n/2 = 15
15 से ठीक अधिक संचयी बारंबारता 19 है, जो वर्ग अन्तराल 55-60 से संबंधित है।
निम्न सीमा, l = 55
n = 30
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता, cf = 13
माध्यक वर्ग की बारंबारता, f = 6
वर्ग माप, h = 5
माध्यक = l + (n/2 − cf)/f × h
= 55 + (15 − 13)/6 × 5
= 55 + 2/6 × 5
= 55 + 5/3
= 55 + 1.67
= 56.67
अतः माध्यक भार 56.67 कि०ग्रा० है।
The distribution below gives the weights of 30 students of a class. Find the median weight of the students :
| Weight (in kg) | No. of Students |
| 40-45 | 2 |
| 45-50 | 3 |
| 50-55 | 8 |
| 55-60 | 6 |
| 60-65 | 6 |
| 65-70 | 3 |
| 70-75 | 2 |
Answer :
| Weight (in kg) Class Interval | No. of Students (f) | Cumulative frequency (cf) |
| 40-45 | 2 | 2 |
| 45-50 | 3 | 2+3=5 |
| 50-55 | 8 | 5+8=13 |
| 55-60 | 6 | 13+6=19 |
| 60-65 | 6 | 19+6=25 |
| 65-70 | 3 | 25+3=28 |
| 70-75 | 2 | 28+2=30 |
Total frequency, n = 30 → n/2 = 15
The cumulative frequency just greater than 15 is 19, which corresponds to the class interval 55-60.
Lower limit, l = 55
n = 30
Cumulative frequency, cf = 13
Frequency of the median class, f = 6
Class size, h = 5
Median = l + (n/2 − cf)/f × h
= 55 + (15 − 13)/6 × 5
= 55 + 2/6 × 5
= 55 + 5/3
= 55 + 1.67
= 56.67
Hence, the median weight is 56.67 kg.
SECTION – E (3 Marks : CASE STUDY)
36. नीचे दिए गए चित्र में दिखाए अनुसार एक त्रिकोणीय खेल का मैदान है।
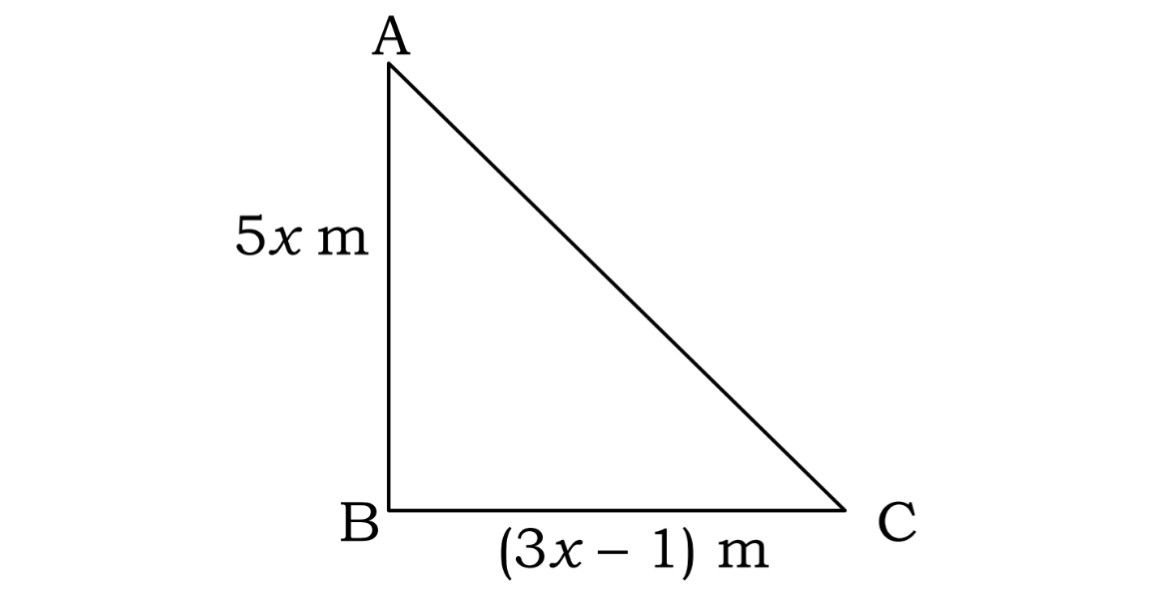
जैसा कि हम समकोण त्रिभुजाकार खेल के मैदान की उपरोक्त आकृति में देखते हैं भुजाओं की लंबाई 5x मी० तथा (3x – 1) मी० है और त्रिभुज का क्षेत्रफल 60 मी०2 है।
उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) उपरोक्त प्रश्न को एक द्विघात समीकरण के रूप में व्यक्त कीजिए।
उत्तर : ऊँचाई, AB = 5x मी०
आधार, BC = (3x – 1) मी०
क्षेत्रफल = 60 मी०2
क्षेत्रफल = 1/2 × आधार × ऊँचाई
60 = 1/2 × (3x – 1) × 5x
120 = 15x2 – 5x
15x2 – 5x – 120 = 0
3x2 – x – 24 = 0
(ii) x का मान ज्ञात कीजिए।
उत्तर : 3x2 – x – 24 = 0
3x2 – 9x + 8x – 24 = 0
3x(x – 3) + 8(x – 3) = 0
(x – 3)(3x + 8) = 0
x = 3 (अस्वीकार करें x ≠ –8/3 को)
अथवा
AC की लंबाई ज्ञात कीजिए।
उत्तर : ऊँचाई, AB = 5x = 5(3) = 15 मी०
आधार, BC = 3x – 1 = 3(3) – 1 = 8 मी०
पाइथागोरस प्रमेय का प्रयोग करते हुए,
AC2 = AB2 + BC2
AC2 = 152 + 82 = 225 + 64 = 289 = 172
AC = 17 m
(iii) ∆ABC का परिमाप ज्ञात कीजिए।
उत्तर : परिमाप = AB + BC + AC
= 15 + 8 + 17
= 40 m
There is a triangular playground as shown in the figure below :

As we see in the above figure of right angled triangular playground, the length of the sides are 5x m and (3x – 1) m and area of the triangle is 60 m2.
Based on the above information, answer the following questions :
(i) Represent the above problem in the form of a quadratic equation.
Answer : Height, AB = 5x m
Base, BC = (3x – 1) m
Area = 60 m2
Area = 1/2 × base × height
60 = 1/2 × (3x – 1) × 5x
120 = 15x2 – 5x
15x2 – 5x – 120 = 0
3x2 – x – 24 = 0
(ii) Find the value of x.
Answer : 3x2 – x – 24 = 0
3x2 – 9x + 8x – 24 = 0
3x(x – 3) + 8(x – 3) = 0
(x – 3)(3x + 8) = 0
x = 3 (Reject x ≠ –8/3)
OR
Find the length of AC.
Answer : Height, AB = 5x = 5(3) = 15 m
Base, BC = 3x – 1 = 3(3) – 1 = 8 m
Using the Pythagorean theorem,
AC2 = AB2 + BC2
AC2 = 152 + 82 = 225 + 64 = 289 = 172
AC = 17 m
(iii) Find the perimeter of ∆ABC.
Answer : Perimeter = AB + BC + AC
= 15 + 8 + 17
= 40 m
37. साइकिलों की चेन या पुल्ली के चारों ओर बेल्ट, वृत्त की स्पर्श रेखाओं के वास्तविक जीवन के उदाहरण हैं। जैसा कि संलग्न चित्र में दिखाया गया है।
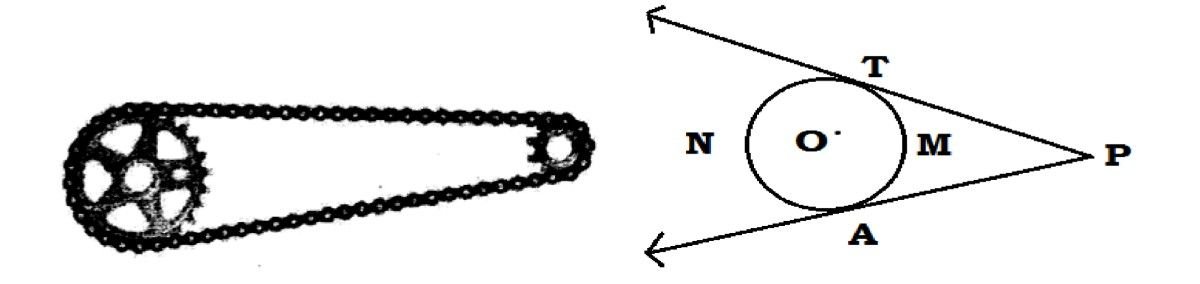
उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) यदि TP = 39 और AP = x2 + 3, तो x का मान ज्ञात कीजिए।
उत्तर : TP = AP (स्पर्श रेखाओं की लंबाई बराबर होती है)
39 = x2 + 3
x2 = 39 – 3 = 36 = 62
x = 6
(ii) PT और PA बिन्दु P से वृत्त पर स्पर्श रेखाएँ हैं। यदि चाप TMA वृत्त के केन्द्र पर 120° का कोण अन्तरित करती है, तो ∠TPA ज्ञात कीजिए।
उत्तर : दो स्पर्श रेखाओं के बीच का कोण = 180° – केंद्र पर बना कोण
∠TPA = 180° – ∠TOA = 180° – 120° = 60°
(iii) चाप TNA और चाप TMA के माप का अनुपात ज्ञात कीजिए।
उत्तर : लघु चाप TMA का माप = 120°
दीर्घ चाप TNA का माप = 360° – 120° = 240°
TNA और TMA का अनुपात = चाप TNA : चाप TMA = 240° : 120° = 2 : 1
अथवा
यदि TP = 20 सेमी है, तो AT ज्ञात कीजिए।
उत्तर : त्रिभुज ∆TPA में, TP = AP और ∠TPA = 60°
शेष दो कोण भी (180°–60°)/2 = 60° होने चाहिए।
अतः त्रिभुज TPA एक समबाहु त्रिभुज है।
इसलिए, AT = 20 cm
The chain of bicycles or belt around pulleys are some real life illustrations of tangents to a circle as shown in the adjoining figure.

Based on the given information, answer the following questions :
(i) If TP = 39 and AP = x2 + 3, then find the value of x.
Answer : TP = AP (lengths of tangents are equal)
39 = x2 + 3
x2 = 39 – 3 = 36 = 62
x = 6
(ii) PT and PA are tangents to the circle from point P. If arc TMA subtends an angle 120° at the centre of the circle, then find ∠TPA.
Answer : Angle between two tangents = 180° – angle subtended at centre
∠TPA = 180° – ∠TOA = 180° – 120° = 60°
(iii) Find the ratio of measures of arcs TNA and TMA.
Answer : The measure of the minor arc TMA = 120°
The measure of the major arc TNA = 360° – 120° = 240°
The ratio of TNA to TMA = arc TNA : arc TMA = 240° : 120° = 2 : 1
OR
If TP = 20 cm, then find AT.
Answer : In ∆TPA, TP = AP and ∠TPA = 60°
The remaining two angles must also (180°–60°)/2 = 60°
Thus, ∆TPA is an equilateral triangle.
so, AT = 20 cm
38. दो सहेलियों सोनिया और श्रुति के पास गुल्लक में कुछ बचत है। उन्होंने अपने पास मौजूद कुल सिक्कों को गिनने का फैसला किया। गिनने के बाद, उन्होंने पाया कि उनके पास ₹1 के 60 सिक्के, ₹2 के 42 सिक्के, ₹5 के 30 सिक्के, ₹10 के 35 सिक्के और ₹20 के 12 सिक्के हैं। अब उन्होंने अपनी एक सहेली सलोनी से यादृच्छया एक सिक्का चुनने को कहा।

उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) क्या प्रायिकता है कि चुना गया सिक्का ₹2 का है?
उत्तर : ₹1 के सिक्के = 60
₹2 के सिक्के = 42
₹5 के सिक्के = 30
₹10 के सिक्के = 35
₹20 के सिक्के = 12
कुल सिक्के, n(S) = 60 + 42 + 30 + 35 + 12 = 179
P(E) = (अनुकूल परिणामों की संख्या) / (कुल परिणामों की संख्या)
P(₹2 का सिक्का) = 42/179
(ii) क्या प्रायिकता है कि चुना गया सिक्का ₹5 का नहीं है?
उत्तर : कुल सिक्के = 179
₹5 के अलावा अन्य सिक्के = 179 – 30 = 149
P(₹5 के अलावा अन्य सिक्का) = 149/179
(iii) क्या प्रायिकता है कि चुना गया सिक्का ₹10 या ₹20 का है?
उत्तर : ₹10 या ₹20 के सिक्के = 35 + 12 = 47
P(₹10 या ₹20 का सिक्का) = 47/179
अथवा
क्या प्रायिकता है कि चुना गया सिक्का ₹10 से कम रुपये का है?
उत्तर : ₹1 के सिक्के = 60
₹2 के सिक्के = 42
₹5 के सिक्के = 30
₹10 से कम के सिक्के = 60 + 42 + 30 = 132
P(₹10 से कम के सिक्का) = 132/179
Two friends Soniya and Shruti have some savings in their Piggi Bank. They decided to count the total coins they both had. After counting, they find that they have sixty ₹1 coins, forty two ₹2 coins, thirty ₹5 coins, thirty five ₹10 coins, and twelve ₹20 coins. Now they said to Saloni, their another friend, to choose a coin randomly.

Based on the above information, answer the following questions :
(i) What is the probability that the coin chosen is a ₹2 coin?
Answer : ₹1 coins = 60
₹2 coins = 42
₹5 coins = 30
₹10 coins = 35
₹20 coins = 12
Total coins, n(S) = 60 + 42 + 30 + 35 + 12 = 179
P(E) = (No. of favourable outcomes) / (Total no. of outcomes)
P(₹2 coin) = 42/179
(ii) What is the probability that the coin chosen is not a ₹5 coin?
Answer : Total coins = 179
Coins which are not ₹5 = 179 – 30 = 149
P(coin not ₹5) = 149/179
(iii) What is the probability that the coin chosen is either of ₹10 or ₹20 coin?
Answer : Coins of ₹10 or ₹20 = 35 + 12 = 47
P(coin ₹10 or ₹20) = 47/179
OR
What is the probability that the coin chosen is less than ₹10 coin?
Answer : ₹1 coins = 60
₹2 coins = 42
₹5 coins = 30
Less than ₹10 coin = 60 + 42 + 30 = 132
P(coin less than ₹10) = 132/179
