Haryana Board (HBSE) Class 9 Maths Half Yearly Question Paper 2024 PDF Download. HBSE Class 9 Maths Half Yearly Question Paper 2024. Haryana Board Class 9 Mathematics Half Yearly Exam 2024. HBSE Class 9th Math Half Yearly Paper 2024 Answer. Haryana Board Class 9 Half Yearly Paper PDF Download. Haryana Board Class 9 Maths Half Yearly Paper 2024 Solution. हरियाणा बोर्ड कक्षा 9 गणित अर्धवार्षिक पेपर 2024.
HBSE Class 9 Maths Half Yearly Question Paper 2024 Answer Key
Instructions :
• All questions are compulsory.
• Questions (1-11) carry 1 mark each.
• Questions (12-14) carry 2 marks each.
• Questions (15-17) carry 3 marks each.
• Questions (18-19) carry 5 marks each.
• Question (20) case study, carry 4 marks.
1. बहुपद 5x3 + 4x2 + 7x की घात है :
(a) 0
(b) 5
(c) 4
(d) 3
उत्तर : (d) 3
Degree of the polynomial 5x3 + 4x2 + 7x is :
(a) 0
(b) 5
(c) 4
(d) 3
Answer : (d) 3
2. निम्नलिखित में से किसको प्रमाण की आवश्यकता है?
(a) परिभाषा
(b) स्वयंसिद्ध
(c) प्रमेय
(d) अभिधारणा
उत्तर : (c) प्रमेय
Which of the following needs a proof?
(a) Definition
(b) Axiom
(c) Theorem
(d) Postulate
Answer : (c) Theorem
3. निम्नलिखित में से कौन-सी संख्या एक अपरिमेय संख्या है?
(a) √23
(b) √225
(c) 0.3796
(d) 7.478478….
उत्तर : (a) √23
Which of the following numbers is an irrational number?
(a) √23
(b) √225
(c) 0.3796
(d) 7.478478….
Answer : (a) √23
4. दो दिए गए बिन्दु से कितनी रेखाएँ गुजर सकती हैं?
(a) 1
(b) 2
(c) 4
(d) अनंत
उत्तर : (a) 1
How many lines can pass through two given points?
(a) 1
(b) 2
(c) 4
(d) Infinite
Answer : (a) 1
5. x3 + x किस प्रकार का बहुपद है?
(a) रैखिक
(b) द्विघाती
(c) त्रिघाती
(d) इनमें से कोई नहीं
उत्तर : (c) त्रिघाती
Which type of polynomial is x3 + x ?
(a) Linear
(b) Quadratic
(c) Cubic
(d) None of these
Answer : (c) Cubic
6. √2x – 1 में x2 का गुणांक है :
(a) 1
(b) 0
(c) 2
(d) √2
उत्तर : (b) 0
The coefficient of x2 in √2x – 1 is :
(a) 1
(b) 0
(c) 2
(d) √2
Answer : (b) 0
7. दिए गए डेटा में उच्चतम और निम्नतम मानों के बीच के अंतर को क्या कहते है?
उत्तर : परिसर
What is the difference between the highest and lowest values in the given data?
Answer : Range
8. π एक परिमेय संख्या है। (सत्य / असत्य)
π is a rational number. (True / False)
Answer : False
9. मूल के निर्देशांक ………… हैं।
Coordinates of origin are ………….
Answer : (0, 0)
10. यदि किसी त्रिभुज की तीन भुजाएं बराबर हो तो उसे …………. त्रिभुज कहते हैं।
उत्तर : समबाहु त्रिभुज
If three sides of a triangle are equal, then it is called ……………
Answer : Equilateral triangle
11. अभिकथन (A) : दो अपरिमेय संख्याओं 2 + √3 और 4 + √3 का योग एक अपरिमेय संख्या है।
कारण (R) : दो अपरिमेय संख्याओं का योग सदैव एक अपरिमेय संख्या होता है।
उत्तर : अभिकथन (A) और कारण (R) दोनों सही हैं तथा कारण (R), अभिकथन (A) का सही स्पष्टीकरण है।
Assertion (A) : Sum of two irrational numbers 2 + √3 and 4 + √3 is an irrational number.
Reason (R) : The sum of two irrational numbers is always an irrational number.
Answer : Both Assertion (A) and Reason (R) are correct and Reason (R) is the correct explanation for Assertion (A).
12. गुणनखंड कीजिए : x2 – 5x + 6
Factorise : x2 – 5x + 6
Answer : x2 – 5x + 6
= x2 – 3x – 2x + 6
= x(x – 3) – 2(x – 3)
= (x – 3)(x – 2)
13. 1 और 2 के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।
उत्तर : 1 और 2 के बीच अनंत परिमेय संख्याएँ है।
दोनों संख्याओं को 6 से गुणा और भाग करें,
1 × 6/6, 2 × 6/6
6/6, 12/6
इसलिए, 1 और 2 के बीच की पाँच परिमेय संख्याएँ 7/6, 8/6, 9/6, 10/6, 11/6 हैं।
Find five rational numbers between 1 and 2.
Answer : Infinite rational numbers between 1 and 2.
Multiply and divide the both numbers by 6,
1 × 6/6, 2 × 6/6
6/6, 12/6
so, the five rational numbers between 1 and 2 are 7/6, 8/6, 9/6, 10/6, 11/6.
14. Factorise : 8x3 + y3 + 27z3 – 18xyz
गुणनखंड कीजिए : 8x3 + y3 + 27z3 – 18xyz
Answer : 8x3 + y3 + 27z3 – 18xyz
= (2x)3 + (y)3 + (3z)3 – 3(2x)(y)(3z)
Using identity, a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
= (2x + y + 3z)[(2x)2 + (y)2 + (3z)2 – (2x)(y) – (y)(3z) – (3z)(2x)]
= (2x + y + 3z)(4x2 + y2 + 9z2 – 2xy – 3yz – 6zx)
15. हर का परिमेयकरण कीजिए : 1/(√5+√2)
Rationalise the denominator of 1/(√5+√2)
Answer : 1/(√5+√2) × (√5–√2)/(√5–√2)
= 1(√5–√2) / (√5+√2)(√5–√2)
Using identity, (a + b)(a – b) = a² – b²
= 1(√5–√2) / (√5+√2)(√5–√2)
= (√5–√2) / [(√5)²–(√2)²]
= (√5–√2) / (5–2)
= (√5–√2) / 3
16. निम्नलिखित अवलोकनों को आरोही क्रम में व्यवस्थित किया गया है। यदि डेटा का माध्यिका 63 है, तो x का मान ज्ञात करें।
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x :
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Answer : Median = [x+(x+2)] / 2 = 63
2x + 2 = 63 × 2
2x + 2 = 126
2x = 126 – 2
2x = 124
x = 124/2 = 62
17. यदि (x – 1), 4x3 + 3x2 – 4x + k का एक गुणनखंड है तो k का मान ज्ञात कीजिये।
Find the value of k, if (x – 1) is a factor of 4x3 + 3x2 – 4x + k.
Answer : Here x – 1 = 0 so x = 1
Put x = 1 in P(x) = 4x3 + 3x2 – 4x + k
4(1)3 + 3(1)2 – 4(1) + k= 0
4 + 3 – 4 + k = 0
k = –3
18. 0.4777….. को p/q के रूप में व्यक्त करें, जहां p और q दोनों पूर्णांक हों तथा q ≠ 0.
उत्तर : x = 0.4777….. (i)
10x = 4.7777….. (ii)
समीकरण (ii) में से (i) को घटाए,
10x – x = 4.7777….. – 0.4777…..
9x = 4.3
x = 4.3/9 = 43/90
Express 0.4777….. in the form p/q where p and q are integers and q ≠ 0.
Answer : x = 0.4777….. (i)
10x = 4.7777….. (ii)
Subtract eqn.(i) from (ii),
10x – x = 4.7777….. – 0.4777…..
9x = 4.3
x = 4.3/9 = 43/90
19. एक त्रिभुजाकार भूखंड की भुजाओं का अनुपात 3 : 5 : 7 हैं और इसका परिमाप 300 मीटर है। इस भूखंड का क्षेत्रफल ज्ञात कीजिए।
उत्तर : यहां, a = 3x, b = 5x, c = 7x
परिमाप (P) = a + b + c
3x + 5x + 7x = 300
15x = 300
x = 300/15 = 20
a = 3x = 3 × 20 = 60 m
b = 5x = 5 × 20 = 100 m
c = 7x = 7 × 20 = 140 m
अर्ध परिमाप (s) = 300/2 = 150 m
क्षेत्रफल = √s(s–a)(s–b)(s–c)
= √150(150–60)(150–100)(150–140)
= √150(90)(50)(10)
= 1500√3 m2
The sides of a triangular plot are in a ratio of 3 : 5 : 7 and its perimeter is 300 m. Find its area.
Sides of a triangle are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find the area of the triangle.
Answer : Take, a = 3x, b = 5x, c = 7x
Perimeter (P) = a + b + c
3x + 5x + 7x = 300
15x = 300
x = 300/15 = 20
a = 3x = 3 × 20 = 60 m
b = 5x = 5 × 20 = 100 m
c = 7x = 7 × 20 = 140 m
Semi Perimeter (s) = 300/2 = 150 m
Using Heron’s Formula,
Area = √s(s–a)(s–b)(s–c)
= √150(150–60)(150–100)(150–140)
= √150(90)(50)(10)
= 1500√3 m2
20. दसवीं कक्षा के कक्षा शिक्षक एक छात्र का परिणाम विश्लेषण तैयार कर रहे हैं। वह नीचे दिखाए गए अनुसार द्वि-दण्ड आलेख का उपयोग करके कक्षा IX (2018-19) और कक्षा X (2019-20) में प्राप्त एक छात्र के अंकों की तुलना करती है :
The Class teacher of Class X prepares the result analysis of a student. She compares the marks of a student obtained in Class IX (2018-19) and Class X (2019-20) using the graph as shown below :
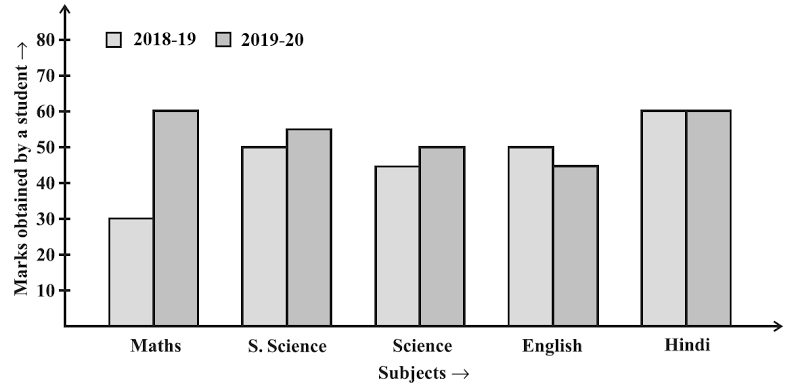
(i) किस विषय में प्रदर्शन में सबसे अधिक सुधार हुआ है?
In which subject has the performance improved the most?
(a) Maths
(b) Social Science
(c) Science
(d) English
Answer : (a) Maths
(ii) किस विषय में प्रदर्शन खराब हुआ है?
In which subject has the performance deteriorated?
(a) Maths
(b) Social Science
(c) Science
(d) English
Answer : (d) English
(iii) किस विषय में प्रदर्शन बराबर है?
In which subject is the performance at par?
(a) Hindi
(b) Maths
(c) Science
(d) English
Answer : (a) Hindi
(iv) गणित विषय में क्या अंतर है?
What is the difference in Maths Subject?
(a) 5
(b) 30
(c) 0
(d) 10
Answer : (b) 30
