Class 9 Maths Half Yearly Question Paper 2025 Answer Key (NCERT Based)
Instructions :
• All questions are compulsory.
• Questions (1-11) carry 1 mark each.
• Questions (12-14) carry 2 marks each.
• Questions (15-17) carry 3 marks each.
• Questions (18-19) carry 5 marks each.
• Question (20) case study, carry 4 marks.
1. एक संख्या अपरिमेय होती है यदि उसका दशमलव निरूपण है :
(a) असांत
(b) अनवसानी अनावर्ती
(c) सांत
(d) अनवसानी आवर्ती
उत्तर : (b) अनवसानी अनावर्ती
A number is irrational if its decimal representation is :
(a) non-terminating
(b) non-terminating, non-recurring
(c) terminating
(d) non-terminating recurring
Answer : (b) non-terminating, non-recurring
2. बहुपद 5x – 4x2 + 3 का मान x = 0 पर ज्ञात करो।
Find the value of the polynomial 5x – 4x2 + 3 at x = 0.
(a) 0
(b) 1
(c) 2
(d) 3
Answer : (d) 3
5x – 4x2 + 3 = 5(0) – 4(0)2 + 3 = 0 – 0 + 3 = 3
3. बिंदु (3, 0) किस अक्ष पर स्थित है :
The point (3, 0) lies on ………
(a) on x-axis
(b) on y-axis
(c) on origin
(d) none of these
Answer : (a) on x-axis
4. k का मान जात कीजिए, यदि x = 1, y = 2 समीकरण 2x + 3y = k का एक हल है।
The value of k if x = 1, y = 2 solution of the equation 2x + 3y = k is :
(a) 7
(b) 8
(c) 6
(d) 1
Answer : (b) 8
k = 2x + 3y = 2(1) + 3(2) = 2 + 6 = 8
5. निम्नलिखित कथनों में से कौन सही है?
(a) अभिगृहीत ऐसे (प्रस्ताव) साध्य होते हैं जिन्हे मान लिया जाता है।
(b) अभिगृहीत विशेष प्रमेय है।
(c) अभिगृहीत परिभाषाएँ हैं।
(d) अभिगृहीत, सिद्ध होने पर प्रमेय बन जाता है।
उत्तर : (a) अभिगृहीत ऐसे (प्रस्ताव) साध्य होते हैं जिन्हे मान लिया जाता है।
Which of the statements are correct?
(a) Axioms are propositions which are assumed.
(b) Axioms are special theorems.
(c) Axioms are definitions.
(d) Axioms when proved become theorems.
Answer : (a) Axioms are propositions which are assumed.
6. बहुपद 2 – x2 + x3 में x2 का गुणांक हैं :
The coefficient of x2 in polynomial 2 – x2 + x3 is :
(a) –1
(b) 1
(c) 2
(d) –2
Answer : (a) –1
7. वर्ग 120-160 का वर्ग चिन्ह लिखे।
Write the class-mark of the class120-160.
Answer : (120+160)/2 = 280/2 = 140
8. हल करे।
Simplify : (32)1/5
Answer : (32)1/5 = (25)1/5 = (2)5 × 1/5 = 2
9. यूक्लिड के अभिधारणाओं की संख्या …………. है।
There are ………….. number of Euclid’s postulates.
Answer : 5
10. समीकरण 2x + 1 = x + 3 का हल ………… है।
The solution of the equation 2x + 1 = x + 3 is :
Answer : 2x – x = 3 – 1
x = 2
11. अभिकथन (A) : बिंदु A(–7, –9) तृतीय चतुर्थांश पर स्थित है।
कारण (R) : एक बिंदु जिसके दोनों निर्देशांक ऋणात्मक हैं, तृतीय चतुर्थांश में स्थित है।
(क) अभिकथन (A) और कारण (R) दोनों सही है और कारण (R), कथन (A) की सही व्याख्या करता है।
(ख) अभिकथन (A) और कारण (R) दोनों सही है लेकिन कारण (R) कथन (A) की सही व्याख्या नहीं करता।
(ग) अभिकथन (A) सही है लेकिन कारण (R) गलत है।
(घ) अभिकथन (A) गलत है लेकिन कारण (R) सही है।
उत्तर : (क) अभिकथन (A) और कारण (R) दोनों सही है और कारण (R), कथन (A) की सही व्याख्या करता है।
Assertion (A) : Point A(–7, –9) lies on the 3rd quadrant.
Reason (R) : A point both of whose coordinates are negative lies in the 3rd quadrant.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true but Reason (R) is false.
(D) Assertion (A) is false but Reason (R) is true.
Answer : (A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
12. हर का परिमेयकरण कीजिए :
Rationalize the denominator: 1/(√5 + √2)
Answer : Divide and multiply by (√5 + √2)
= 1/(√5 + √2) × (√5 – √2)/(√5 – √2)
= (√5 – √2)/(√52 – √22)
= (√5 – √2)/(5 – 2) [using a2 – b2 = (a – b)(a + b)]
= (√5 – √2)/3
13. गणित की एक परीक्षा में 17 छात्रों द्वारा प्राप्त अंक (100 में से) नीचे दिए गए हैं 98, 82, 100, 100, 96, 65, 82, 76, 79, 90, 41, 64, 72, 68, 66, 48, 49 आंकड़ों की परिसर ज्ञात कीजिए।
The marks obtained by 17 students in a mathematics test (out of 100) are given below
98, 82, 100, 100, 96, 65, 82, 76, 79, 90, 41, 64, 72, 68, 66, 48, 49
Find the range of the data.
Answer : Highest marks = 100
Lowest marks = 41
Range = Highest marks – Lowest marks = 100 – 41 = 59
14. निम्नलिखित बिंदु के निर्देशांक जात करें :
Find coordinates of the following points :
(i) कोटि (–10) है और भुज (+5) है
ordinate is (–10) and abscissa is (+5)
Answer : (5, –10)
(ii) +6 (y-अक्ष) पर स्थित है
+6 lies on y-axis
Answer : (0, 6)
15. Factorise : 2x2 – 7x – 15
गुणनखंड कीजिए : 2x2 – 7x – 15
Answer : 2x2 – 7x – 15
= 2x2 – 10x + 3x – 15
= 2x(x – 5) + 3(x – 5)
= (x – 5)(2x + 3)
16. समीकरण 2x + y = 6 के चार भिन्न हल जात कीजिए।
Find four different solutions of equation 2x + y = 6.
Answer : There are infinite solutions of this equation y = 6 – 2x
Taking x = 0 then y = 6 – 2(0) = 6
Taking x = 1 then y = 6 – 2(1) = 4
Taking x = 2 then y = 6 – 2(2) = 2
Taking x = 3 then y = 6 – 2(3) = 0
Hence (0, 6), (1, 4), (2, 2) and (3, 0) are four solutions of the given equation.
17. सीधे गुणा किए बिना 105 × 106 का मूल्यांकन कीजिए।
Evaluate 105 × 106 without multiplying directly.
Answer : 105 × 106 = (100 + 5)(100 + 6)
Using identity (x + a)(x + b) = x2 + (a + b)x + ab
= (100)2 + (5 + 6) × 100 + (5)(6)
= 10000 + 1100 + 30
= 11130
18. निम्नलिखित अवलोकनों को आरोही क्रम में व्यवस्थित किया गया है। यदि डेटा का माध्यिका 63 है, तो x का मान ज्ञात करें।
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Answer : Median = [x + (x+2)] ÷ 2 = 63
2x + 2 = 63 × 2
2x + 2 = 126
2x = 126 – 2
2x = 124
x = 124/2
x = 62
19. यदि किसी त्रिभुज की भुजाएँ 12 : 17 : 25 के अनुपात में हैं और इसका परिमाप 540 से.मी है तो इसका क्षेत्रफल ज्ञात कीजिए।
If the sides of a triangle are in ratio 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
Answer : Take, a = 12x, b = 17x, c = 25x
Perimeter (P) = a + b + c
12x + 17x + 25x = 540
54x = 540
x = 540/54 = 10
a = 12x = 12 × 10 = 120 cm
b = 17x = 17 × 10 = 170 cm
c = 25x = 25 × 10 = 250 cm
Semi Perimeter (s) = 540/2 = 270 cm
Using Heron’s Formula,
Area of triangle = √s(s-a)(s-b)(s-c)
A = √270(270–120)(270–170)(270–250)
= √270(150)(100)(20)
= 9000 cm2
20. केस स्टडी : कक्षा IX के एक विशेष सेक्शन में, 40 छात्रों से उनके जन्म के महीनों के बारे में पूछा गया और प्राप्त आँकड़ों के आधार पर निम्नलिखित ग्राफ़ तैयार किया गया :
CASE STUDY : In a Particular section of IX Class, 40 students were asked about the months of their birth and the following graph was prepared for the data so obtained :
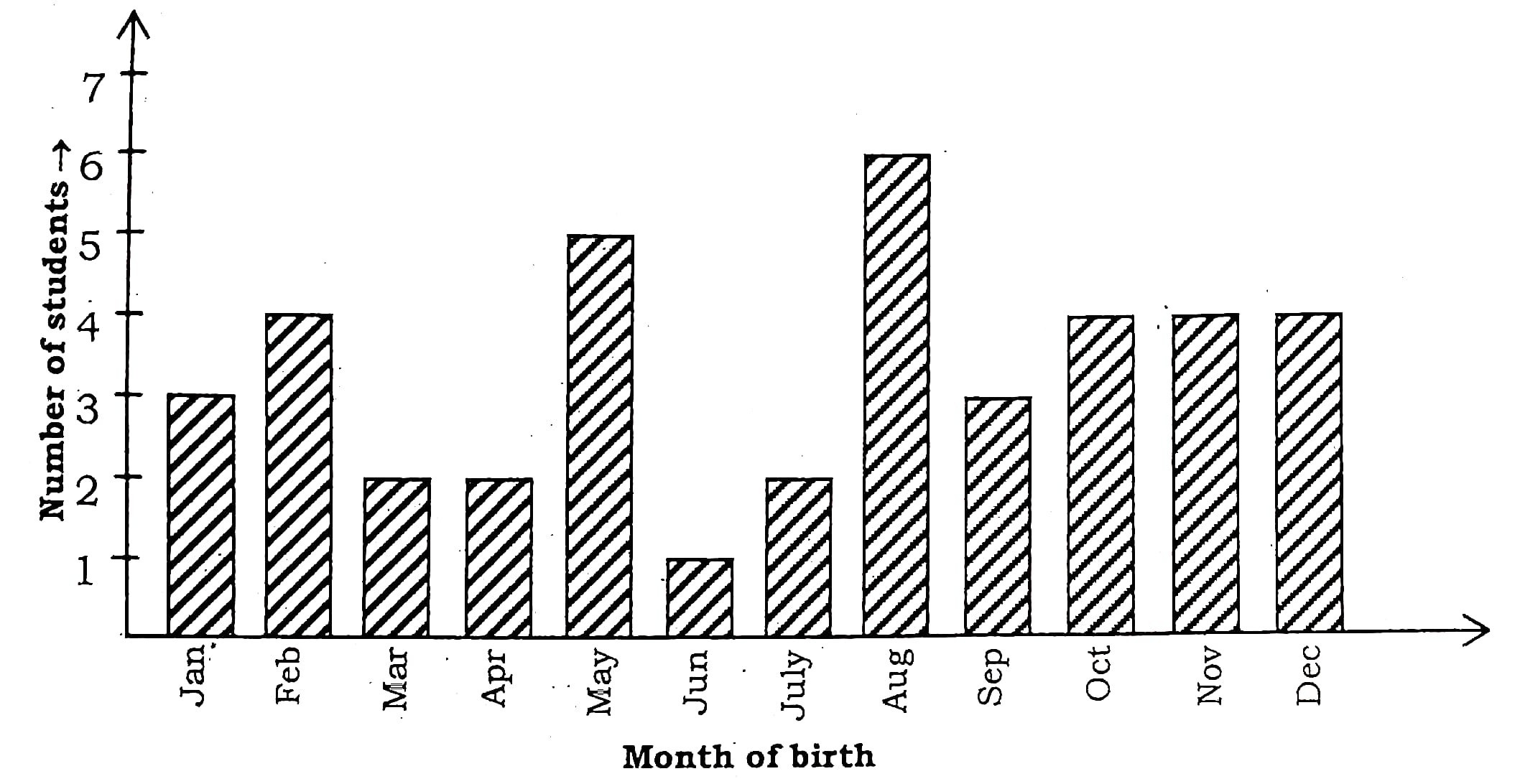
ऊपर दिए गए दंड आलेख का अवलोकन कीजिए और निम्नलिखित प्रश्नों के उत्तर दीजिए :
Observe the bar graph given above and answer the following questions :
(i) नवंबर महीने में कितने छात्रों का जन्म हुआ?
How many students were born in the month of November?
Answer : 4 students
(ii) किस महीने में सबसे अधिक छात्रों का जन्म हुआ?
In which month were the maximum number of students born?
Answer : August
(iii) उस महीने का नाम बताइए जिसमें 4 छात्रों का जन्म हुआ।
Name the month in which 4 students were born.
Answer : Feb, Oct, Nov, Dec
(iv) मई से अगस्त तक जन्मे छात्रों की कुल संख्या ज्ञात कीजिए।
Find the total number of students born from May to August.
Answer : 5 + 1 + 2 + 6 = 14 students
